标签:col span math class image 代码 plain lis max
有形如下图所示的数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的值最大。
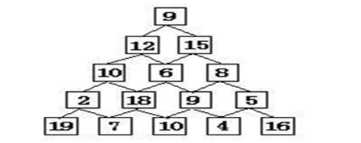
使用动态规划:
从顶点出发,向左走、向右走取决于左边大还是右边大,即
dp[1][1] = max(dp[2][1],dp[2][2])
看似是自顶向下求解,但是问题中存在重复子问题:第一层的最大值是第一层加上第二层的最大值,而第二层的最大值又是与第二层各个元素连接的第三层的元素最大值加上第二层各元素……
所以实际求解是自底向上:
状态转移方程为 dp[i] = max(dp[i+1][j],dp[i+1][j+1]);
代码:
1 #include<iostream> 2 #include<cmath> 3 #include<algorithm> 4 #include<vector> 5 using namespace std; 6 int f[100][100]; 7 int dp[100][100]; 8 int main() 9 { 10 int n; 11 scanf("%d", &n); 12 vector<int>list; 13 for (int i = 1; i <= n; i++) 14 for (int j = 1; j <= i; j++) 15 scanf("%d", &f[i][j]); 16 for (int i = 0; i <= n; i++) 17 dp[n][i] = f[n][i]; 18 for (int i = n - 1; i >= 0; i--) 19 for (int j = i; j >= 0; j--) 20 dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + f[i][j]; 21 22 int max = dp[1][1]; 23 for (int i = 1; i <= n; i++) 24 { 25 for (int j = 1; j <= i; j++) 26 { 27 if (max == dp[i][j]) 28 { 29 list.push_back(f[i][j]); 30 max = max - f[i][j]; 31 } 32 } 33 } 34 35 printf("max amount:%d\n", dp[1][1]); 36 for (int i = 0; i < list.size(); i++) 37 printf("%s%d", i == 0 ? "" : " ", list[i]); 38 } 39 //5 40 //9 12 15 10 6 8 2 18 9 5 19 7 10 4 16
标签:col span math class image 代码 plain lis max
原文地址:https://www.cnblogs.com/Jason66661010/p/12790502.html