标签:nlogn vat ext imp info 试题 com span system
package arithmetic.com.ty.binary; import java.util.Arrays; import java.util.HashMap; import java.util.Random; public class LockData { public static void main(String args[]) { //随机生成1-100的一个数作为缺失数 Random rand = new Random(); int miss=0; miss=rand.nextInt(100)+1; System.out.println("缺失的数为"+miss); //生成缺失了一个数之后的数组 int[] missArray = new int[99]; int j=0; for(int i=1;i<=100;i++) { if(i!=miss) { missArray[j] = i; j++; } } System.out.println("解法一:"+solution1(missArray)); System.out.println("解法二:"+solution2(missArray)); System.out.println("解法三:"+solution3(missArray)); } /*解法一 * 创建一个HashMap,以1到100为键,值都是0 。然后遍历整个数组,每读到一个整数,就找到HashMap当中对应的键,让其值加一。 * 由于数组中缺少一个整数,最终一定有99个键对应的值等于1, 剩下一个键对应的值等于0。遍历修改后的HashMap,找到这个值为0的键。 * 假设数组长度是N,那么该解法的时间复杂度是O(1),空间复杂度是O(N)。**/ public static int solution1(int[] missArray) { int missnumber = 0; //初始化map HashMap<Integer, Integer> myMap = new HashMap<Integer, Integer>(); for(int i=1;i<=100;i++) { myMap.put(i, 0); } //历整个数组,每读到一个整数,就找到HashMap当中对应的键,让其值加一 for(int m:missArray) { myMap.remove(m); } //遍历修改后的HashMap,找到这个值为0的键 for (int key : myMap.keySet()) { if(myMap.get(key)==0) { missnumber = key; break; } } return missnumber; } /* * 解法二: * 先把数组元素进行排序,然后遍历数组,检查任意两个相邻元素数值是否是连续的。如果不连续,则中间缺少的整数就是所要寻找的;如果全都连续,则缺少的整数不是1就是100。 * 假设数组长度是N,如果用时间复杂度为O(N*LogN)的排序算法进行排序,那么该解法的时间复杂度是O(N*LogN),空间复杂度是O(1)。 */ public static int solution2(int[] missArray) { int missnumber = 0; //数组排序 Arrays.sort(missArray); //检查是否相邻 for(int i=0;i<missArray.length-1;i++) { if(missArray[i+1]-missArray[i]!=1) { missnumber=missArray[i]+1; } } //如果检查到相邻则返回否则缺失的数为100 if(missnumber!=0) { return missnumber; } else { return 100; } } /* * 解法三: * 很简单也很高效的方法,先算出1+2+3....+100的合,然后依次减去数组里的元素,最后得到的差,就是唯一缺失的整数。 * 假设数组长度是N,那么该解法的时间复杂度是O(N),空间复杂度是O(1)。 */ public static int solution3(int[] missArray) { int missnumber=0; int all = 0; int missall = 0; for(int i=1;i<=100;i++) { all = all+i; } for(int m:missArray) { missall = missall+m; } return all-missall; } }
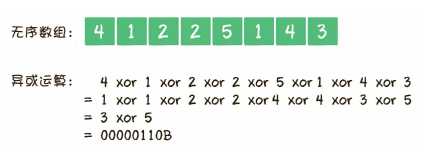
首先得知道异或运算:

代码:
/* * 遍历整个数组,依次做异或运算。由于异或在位运算时相同为0,不同为1,因此所有出现偶数次的整数都会相互抵消变成0,只有唯一出现奇数次的整数会被留下。 * 假设数组长度是N,那么该解法的时间复杂度是O(N),空间复杂度是O(1)。**/ public static int solution2(int[] missArray) { int missnumber = 0; for(int m:missArray) { missnumber = missnumber^m; } return missnumber; }
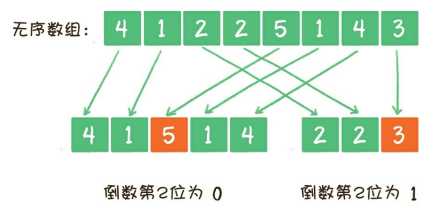
思路:
代码:
public static void solution2(int[] missArray) { int temp = 0; //数组所有元素异或。数组所有元素异或结果其实就是两个奇数次整数的异或结果,因为一个整数出现偶数次,异或一定是0. for(int m:missArray) { temp = temp^m; } int site=1; /* * 找到1位为1的元素。 * 例如无序数组{4,1,2,2,5,1,4,3},异或后的temp=00000110B。 * 1<<site & temp == 0则代表第site位都是0,若果不等于0,说明找到1了。site就是1的位数 */ while((temp & (1 << site))==0) { site++; } int num1 = 0; int num2 = 0; for(int m:missArray) { //根据上面获得到的第site位为1的情况,取第site位为1的所有数,循环做异或,另外一组做异或。保证A、B是分开的 if(getBit(m, site)) { num1 = num1^m; } else { num2 = num2^m; } } System.out.println("奇数的数为"+num1); System.out.println("奇数的数为"+num2); } //获取 整数 num 的第 i 位的值 private static boolean getBit(int num, int i) { //true 表示第i位为1,否则为0。a & b == 1 说明a b都是1 return ((num & (1 << i)) != 0); }
标签:nlogn vat ext imp info 试题 com span system
原文地址:https://www.cnblogs.com/alimayun/p/12793349.html