标签:double 快速 code 快速幂 div class nbsp lse http
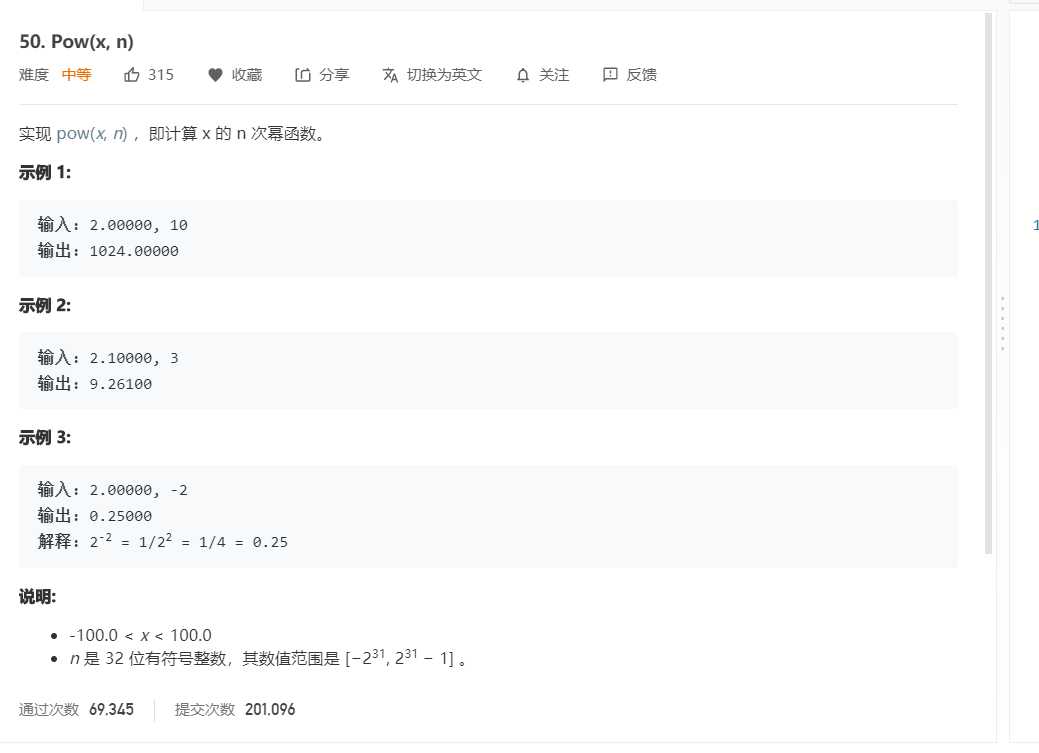
思路:求的是x的n次方,如果是写一个循环,肯定会超时。
假如已经知道了x的n次方,该怎么求x的2n次方呢?肯定不需要循环乘x乘n次了,x的n次方的平方,就等于x的2n次方。
假如求x的n次方,n是偶数,可以先求x的n/2次方,之后求个平方。
假如n是奇数,先求x的n/2次方,再求平方,之后再乘以x就行。
负数的话比较特殊,偶数这里,还是一样的。因为-2%2==0,n为负偶数不用管
负奇数的话,得half*half/x。
class Solution {
//快速幂
double myPow(double x, int n) {
if (n == 0) return 1;
double half = myPow(x, n / 2);
if (n % 2 == 0) return half * half;//n是偶数
if (n > 0) return half * half * x;//n是正奇数
return half * half / x;//n是负奇数
}
};
或者下面的都行
class Solution {
public double myPow(double x, int n) {
if(n==0)
return 1;
double y=myPow(x,n/2);
if(n>0)
{
if(n%2==0)
return y*y;
else
return x*y*y;
}
else
{
if(n%2==0)
return y*y;
else
return 1/x*y*y;
}
}
}
标签:double 快速 code 快速幂 div class nbsp lse http
原文地址:https://www.cnblogs.com/lzh1043060917/p/12800203.html