标签：lis 加载 alt ade 作者 close 相对 文本文件 pychar
Logistic回归算法只能用于预测结果只有两种情况（即要么0，要么1）的实例。而我们需要的函数则是能接收所有输入特征，最后预测出类别。且函数能稳定在某两个值之间，且能够平均分配，这里就引入了数学上的一个函数，即Sigmoid函数。
Sigmoid函数计算公式如下：
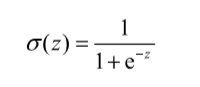
Sigmoid函数图像如下（来源：百度百科-Sigmoid函数）：
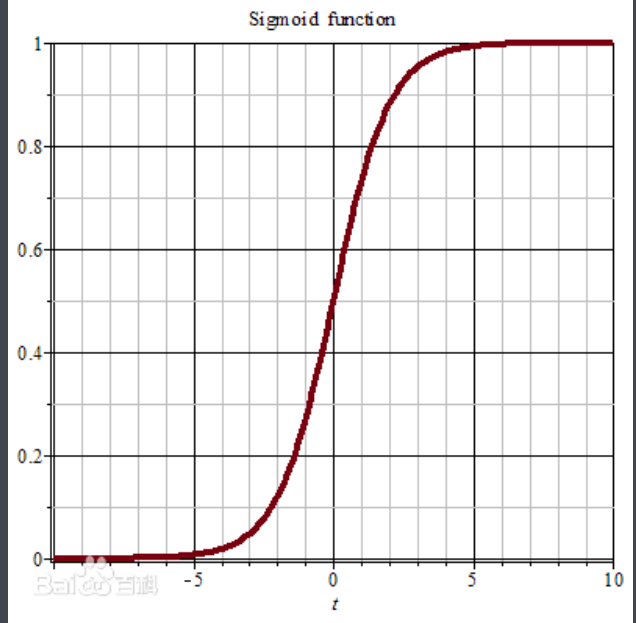
Sigmoid函数特点描述：
当z值为0，Sigmoid函数值为0.5.随着z的不断增大，对应的Sigmoid值将逼近1；而随着z的减小，Sigmoid值将逼近与0。如果横坐标刻度足够大，那么纵观Sigmoid函数，它看起来很像一个阶跃函数。
而Sigmoid函数中的z值是需要经过下列计算的，为了实现Logistic回归分类器，我们可以在每一个特征上乘以一个回归系数，然后把所有的结果值相加，而这个相加的总和就是z值了。再将z值代入到Sigmoid函数中，可以得到一个0到1之间的数值，我们将任何大于0.5的数值归为1类，小于0.5的数值被归为0类。所以，Logistic回归可以被看做是一种概率估算。
在上面说明了z值的计算方法后，我们用公式来更直观地描述z值计算：
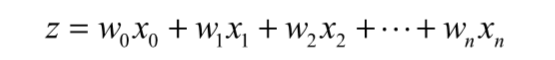
用向量的写法，上述公式可以写成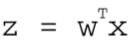
，表示将这两个数值向量对应元素相乘起来然后全部加起来即是z值。其中向量x是分类器的输入数据，即特征值数据；向量w是我们需要寻找的最佳系数，寻找最佳系数的目的是为了让分类器的结果尽可能的精确。
经过上面分析，Sigmoid函数公式最终形式可以写成下面这种形式：
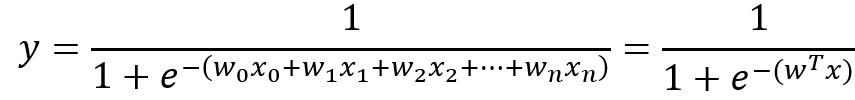
上面我们提到z值计算中，w的值是回归系数，而回归系数决定了预测结果的准确性，为了获取最优回归系数，我们需要使用最优化方法。最优化方法这里学习和使用两种：梯度上升算法和随机梯度上升算法（是对梯度上升算法的改进，使计算复杂度降低）。
算法思想：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。
算法迭代公式：
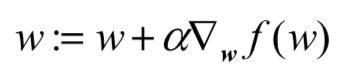
其中：
w是我们要求的最佳系数，因为这个公式要迭代多次，且不断变大直到得到一个最佳系数值，所以每次要在w的基础上加上某个方向的步长。α是步长，即每次的移动量。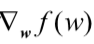
是梯度方向，即每次迭代时w上升最快的方向。def loadDataSet():
"""
读取测试文件中的数据，拆分得到的每一行数据并存入相应的矩阵中，最后返回。
:return: dataMat, labelMat
dataMat: 特征矩阵
labelMat: 类型矩阵
"""
# 初始化特征列表和类型列表
dataMat = []
labelMat = []
# 打开测试数据，默认为读方式
fr = open("data/testSet.txt")
# 通过readLines()方法可以获得文件中的所有行信息
for line in fr.readlines():
# 将一行中大的信息先通过strip()方法去掉首尾空格
# 再通过split()方法进行分割，默认分割方式是空格分割
# 将分割好后的数据存入列表lineArr
lineArr = line.strip().split()
# 取出列表lineArr中的数据通过append方法插入到dataMat列表表中
# 这里为了方便计算，将第一列的值都设置为1.0
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
# 再取出文件中的最后一列的值作为类型值存入labelMat列表中
labelMat.append(int(lineArr[2]))
"""
列表中的append方法小结：
从上面两个列表添加元素的语句可以看出：
当我们需要添加一行数据时，需要加[]，表示将插入一行数据。
当我们将数据直接插入到某一列的后面时，则不需要加[]。
且需要注意的是：如果一次要添加好几个元素时，必须有[],否则会报错。
"""
return dataMat, labelMat
def sigmoid(inX):
"""
sigmoid函数：α(z) = 1 / (1 + e^(-z))
:param inX: 函数中的参数z
:return: 返回函数计算结果
"""
return 1.0 / (1 + exp(-inX))
def gradAscent(dataMatIn, classLabels):
"""
梯度上升算法
:param dataMatIn: 特征值数组
:param classLabels: 类型值数组
:return: 返回最佳回归系数
"""
# 通过numpy模块中的mat方法可以将列表转化为矩阵
dataMatrix = mat(dataMatIn)
# transpose()方法是矩阵中的转置
labelMatrix = mat(classLabels).transpose()
# 通过numpy中大的shape方法可以获得矩阵的行数和列数信息
# 当矩阵是一维矩阵时，返回的是一个数的值
# 当矩阵是二维矩阵时，返回的是一个（1*2）的元组，元组第一个元素表示行数，第二个元素表示列数
m, n = shape(dataMatrix) # m = 100; n = 3
alpha = 0.001 # 步长
maxCycles = 500 # 迭代次数
# ones()属于numpy模块，函数功能是生成一个所有元素都为1的数组
# 这里是生成一个“n行1列”的数组，数组中每一个元素值都是1
weights = ones((n, 1))
# 循环迭代maxCycles次，寻找最佳参数
for k in range(maxCycles):
# dataMatrix * weights 是矩阵乘法
# 矩阵相乘时注意第一个矩阵的列数要和第二个矩阵的行数相同
# (m × n) * ( n × 1) = (m × 1) 括号中表示几行几列
# (100 × 3) * (3 × 1) = (100 × 1)
# 最后得到一个100行1列的矩阵
# 该矩阵运算结果为为sigmoid函数（α(z) = 1 / (1 + e^(-z))）中的z
# z的公式为：z = w0x0 + w1x1 + w2x2 + ... + wnxn
h = sigmoid(dataMatrix * weights)
# 计算真实类别与预测类别的差值
error = labelMatrix - h
# 按差值error的方向调整回归系数
# 0.01 * (3 × m) * (m × 1)
# 表示每一个列上的一个误差情况，最后得到x1，x2，xn的系数偏移量
# 矩阵乘法，最后得到一个更新后的回归系数
# 梯度上升算法公式：w:=w+α▽w f(w)
# 其中α是步长，▽w f(w)是上升方向
weights = weights + alpha * dataMatrix.transpose() * error
return array(weights)
输出：
if __name__ == ‘__main__‘:
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(gradAscent(dataMats, classMats))
print(weights) # 输出最佳系数w的各个值
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
小结：
梯度上升算法核心函数是gradAscent(dataMatIn, classLabels)函数，在该函数中不断迭代使得参数w不断优化，使得最终返回的参数最优。
上述的sigmoid(inX)函数就是我们使用的Sigmoid函数公式，写成函数是因为下面我们会频繁的使用到这个函数，所以将该公式单独封装成一个函数。
loadDataSet()函数作用就是将我们收集到的数据读取出来，并且将读取出来的数据格式化存储到相应的数组中，最后返回供外界使用和分析。
这里小结一下列表中的append()方法和extend()方法：
if __name__ == ‘__main__‘:
li = []
appendLi = [1, 2, 3]
extendLi = [3, 4, 5]
li.append(appendLi)
print(li)
li.extend(extendLi)
print(li)
输出：
[[1, 2, 3]]
[[1, 2, 3], 3, 4, 5]
可以看到append()方法是将appendLi这个列表加入到li列表的新的一行，而extend()方法则是将extendLi列表中的数值取出来一个个接在li列表后面。
这里涉及到的numpy模块中的新函数（所谓新，是相对于我来说滴）：
mat()：将数组或则列表转化为矩阵transpose()方法是矩阵的转置。line.strip().split()用法：可以看到这里是对字符串的切割，字符串line先通过strip()方法去掉了首尾的空格，在通过split()方法进行默认空格切割。两种方法一气呵成，不用分成两不写。
def plotBestFit(dataArr, labelMat, weights):
"""
画出决策边界
:param dataArr: 特征值数组
:param labelMat: 类型数组
:param weights: 最佳回归系数
:return:
"""
# 通过shape函数获得dataArr的行列数，其中[0]即行数
n = shape(dataArr)[0]
# xCord1和yCord1是类型为1的点的x和y坐标值
xCord1 = []
yCord1 = []
# xCord2和yCord1是类型为0的点的x和y坐标值
xCord2 = []
yCord2 = []
# 特征数组的每一行和类型数组的没每一列一一对应
for i in range(n):
# 当类型为1时，
# 将特征数组中的指定行的1和2两个下标下的值分别作为x轴和y轴的值
if int(labelMat[i]) == 1:
xCord1.append(dataArr[i, 1])
yCord1.append(dataArr[i, 2])
# 当类型为0时，
# 将特征数组中的指定行的1和2两个下标下的值分别作为x轴和y轴的值
else:
xCord2.append(dataArr[i, 1])
yCord2.append(dataArr[i, 2])
# figure()操作时创建或者调用画板
# 使用时遵循就近原则，所有画图操作是在最近一次调用的画图板上实现。
fig = plt.figure()
# 将fig分成1×1的网格，在第一个格子中加载ax图
# 参数111表示“1×1网格中的第1个表格”
# 如果参数是211则表示“2行1列的表格的中的第一个表格”
# 第几个表格的计算顺序为从左到右，从上到下
ax = fig.add_subplot(111)
# 设置散点图参数
# 前两个参数xCord1，yCord1表示散点对应的x和y坐标值
# s=30表示散点大小为30
# c=‘red‘表示散点颜色为红色
# marker=‘s‘表示散点的形状，这里是正方形
ax.scatter(xCord1, yCord1, s=30, c=‘red‘, marker=‘s‘)
# 同上说明
ax.scatter(xCord2, yCord2, s=30, c=‘green‘)
# 生成一个[-3.0, 3.0]范围中间隔每0.1取一个值
x = arange(-3.0, 3.0, 0.1)
# y相对于x的函数
"""
这里的y是怎么得到的呢？
从dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
可得：w0*x0+w1*x1+w2*x2 = z
x0最开始就设置为1，x2就是我们画图的y值，x1就是我们画图的x值。
所以：w0 + w1*x + w2*y = 0
→ y = (-w0 - w1 * x) / w2
"""
y = (-weights[0] - weights[1] * x) / weights[2]
# 画线
ax.plot(x, y)
# 设置x轴和y轴的名称
plt.xlabel(‘x1‘)
plt.ylabel(‘x2‘)
# 展示图像
plt.show()
输出：
if __name__ == ‘__main__‘:
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(gradAscent(dataMats, classMats))
plotBestFit(dataArr, classMats, weights) # 调用该函数话决策边界
输出图如下：
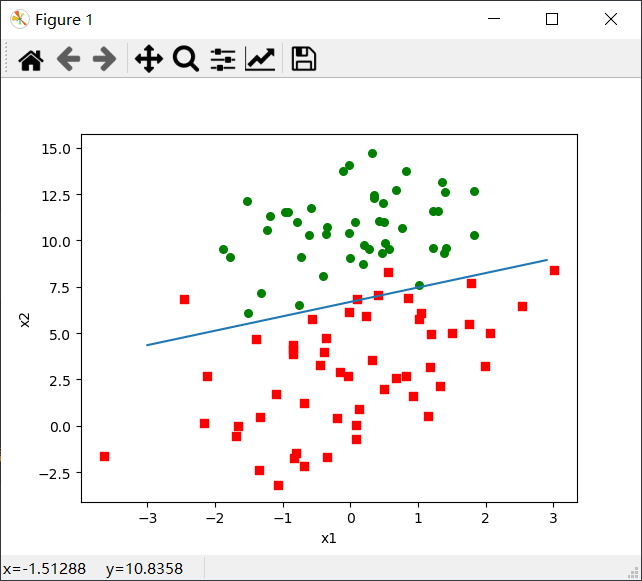
小结：
观察上面的图示，可以看出这个分类结果相当不错，只错分了三四个点。
画图方法小结：(箭头表示赋值)
划分画板→ax：fig.add_subplot(111)方法，其中111表示1*1的画板中的第1个画板。
设置坐标名称：plt.xlabel(‘x1‘)和plt.ylabel(‘x2‘)，这里设置x轴名称为x1，y轴名称为x2。
但是尽管该例子很小且数据集很小，求最佳系数时需要大量的计算（300次乘法）。对于几百个左右的数据集合还可以，但是如果是10亿个样本和成千上万的特征，那么这个计算方法的复杂度太高了，甚至可能出不来最佳系数。所以下面引入随机梯度上升算法。
def stocGradAscent0(dataMatrix, classLabels):
"""
随机梯度上升算法
:param dataMatrix: 特征值矩阵
:param classLabels: 类型数组
:return: 最佳系数weights
"""
# m = 100，n = 3
m, n = shape(dataMatrix)
alpha = 0.01
weights = ones(n)
print(weights)
# 循环迭代m次，即100次
for i in range(m):
# (1 × 3) * (1 × 3) = (1 × 3)
# 数组相乘，两个数组的每个元素对应相乘
# 最后求和
# z = w0x0 + w1x1 + wnxn
# 在将z代入sigmoid函数进行计算
h = sigmoid(sum(dataMatrix[i] * weights))
# 计算实际结果和测试结果之间的误差，按照差值调整回归系数
error = classLabels[i] - h
# 通过梯度上升算法更新weights
weights = weights + alpha * error * dataMatrix[i]
return weights
使用上面的plotBestFit(dataArr, labelMat, weights)函数分析该算法。
输出：
if __name__ == ‘__main__‘:
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(stocGradAscent0(dataArr, classMats))
plotBestFit(dataArr, classMats, weights)
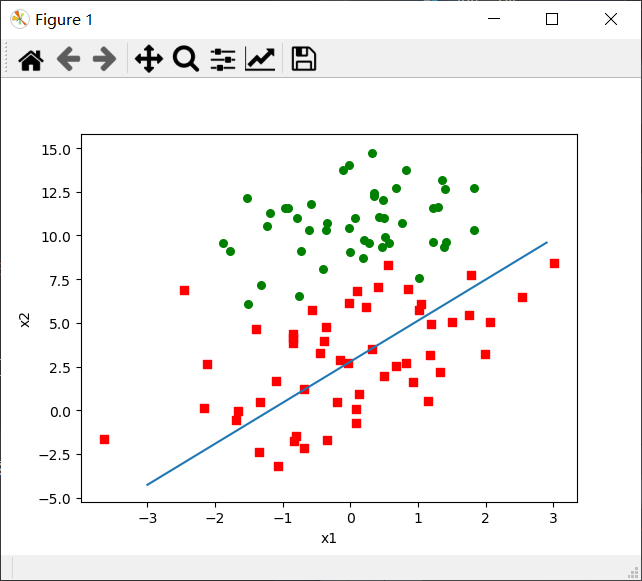
小结：
改进后的随机梯度上升算法代码如下：
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
"""
改进后的随机梯度上升算法
:param dataMatrix: 特征值矩阵
:param classLabels: 类型数组
:param numIter: 迭代次数，设置默认值为150
:return: 最佳系数weights
"""
m, n = shape(dataMatrix)
# 创建与列数相同矩阵，所有元素都为1
weights = ones(n)
# 随机梯度，循环默认次数为150次，观察是否收敛
for j in range(numIter):
# 产生列表为[0, 1, 2 ... m-1]
dataIndex = list(range(m))
for i in range(m):
# i和j不断增大，导致alpha不断减小，单上衣不为0,
# alpha会随着迭代不断的减小，但永远不会减小到0，因为后面还有一个常数项0.01
alpha = 4 / (1.0 + j + i) + 0.01
# 产生一个随机在0-len()之间的值
# random.uniform(x, y)方法将随机生成一个实数，他在[x, y]范围内，x<=y。
randIndex = int(random.uniform(0, len(dataIndex)))
# sum(dataMatrix[randIndex]*weights)是为了求z值
# z = w0x0 + w1x1 + ... + wnxn
h = sigmoid(sum(dataMatrix[randIndex] * weights))
# 计算实际结果和测试结果之间的误差,按照差值调整回归系数
error = classLabels[randIndex] - h
# 通过梯度上升算法更新weights
weights = weights + alpha * error * dataMatrix[randIndex]
# 删除掉此次更新中用到的特征数据
del(dataIndex[randIndex])
return weights
输出：
if __name__ == ‘__main__‘:
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(stocGradAscent1(dataArr, classMats))
plotBestFit(dataArr, classMats, weights)
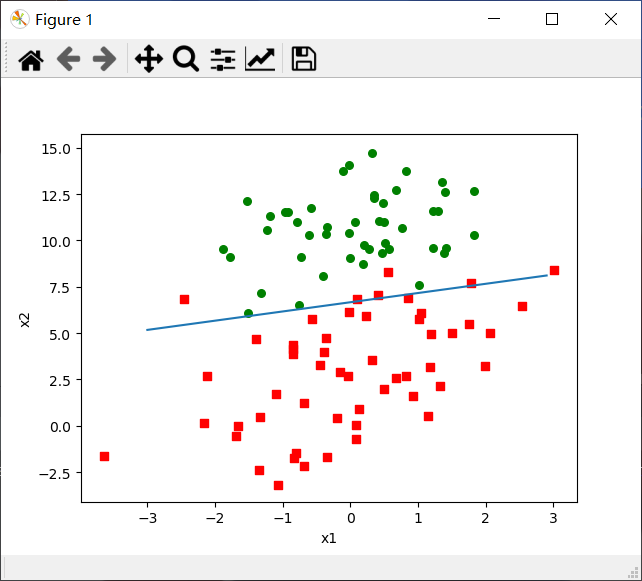
小结：
这里我们将使用Logistic回归来预测患有疝气病症的马的存活问题。这里的数据包含299个训练样本和67个测试样本。其中我们通过21中特征值（每个特征代表什么我们可以不用关心）来进行预测患有疝病的马的存活率。1表示存活，0表示死亡。
训练样本horseColicTraining.txt展示：
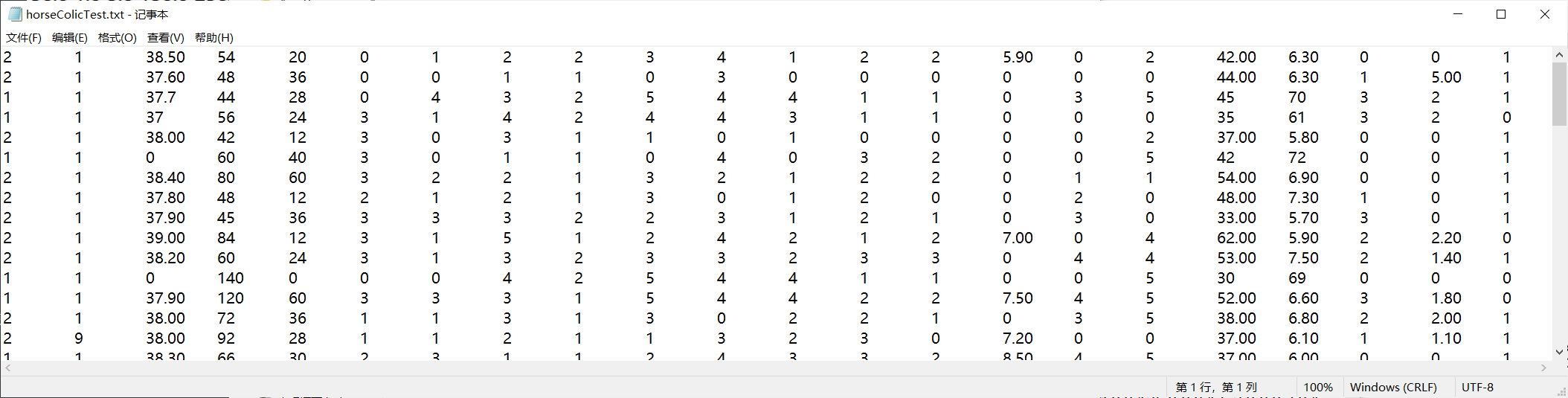
测试样本horseColicTest.txt展示：
测试算法：用Logistic回归进行分类
def classifyVector(inX, weights):
"""
使用梯度上升算法获取到的最优系数来计算测试样本中对应的Sigmoid值。
其中Sigmoid值大于0.5返回1，小于0.5返回0.
:param inX: 特征数组
:param weights: 最优系数
:return: 返回分类结果，即1或0
"""
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def colicTest():
"""
测试回归系数算法的用于计算疝气病症预测病马的死亡率的错误率。
这里运用的随机梯度算法来获取最佳系数w1，w2,...,wn
:return: 返回此次测试的错误率
"""
# 以默认只读方式打开训练数据样本和测试数据样本
frTrain = open(‘data/horseColicTraining.txt‘)
frTest = open(‘data/horseColicTest.txt‘)
trainingSet = []
trainingLabels = []
# 读取训练数据样本的每一行
for line in frTrain.readlines():
# 去掉首尾空格，并按tab空格数来切割字符串，并将切割后的值存入列表
currLine = line.strip().split(‘\t‘)
lineArr = []
# 将21个特征值依次加入到lineArr列表汇总
for i in range(21):
lineArr.append(float(currLine[i]))
# 再将lineArr列表加入到二维列表trainingSet列表中
trainingSet.append(lineArr)
# 将类型值依次接到trainingLabels这个列表的末尾行
trainingLabels.append(float(currLine[21]))
# 使用上面写的改进的随机梯度算法求得最佳系数，用于下面分类器使用区分类型
trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 300)
errorCount = 0
numTestVec = 0.0
# 读取测试数据的每一行
for line in frTest.readlines():
# 测试数据数加1
numTestVec += 1.0
# 去掉首尾空格，并以tab空格数切割字符串，并将切割后的值存入列表
currLine = line.strip().split(‘\t‘)
lineArr = []
# 将21个特征值依次加入到特征列表lineArr中
for i in range(21):
lineArr.append(float(currLine[i]))
# 通过上面计算得到的最佳系数，使用分类器计算lineArr这些特征下的所属的类型
if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]):
# 如果分类器得到结果和真实结果不符，则错误次数加1
errorCount += 1
# 通过遍历获得的所有测试数据量和错误次数求得最终的错误率
errorRate = float(errorCount) / numTestVec
# 输出错误率
print("测试结果的错误率为：{:.2%}".format(errorRate))
# 返回错误率，用于计算n次错误率的平均值
return errorRate
def multiTest():
"""
多次测试算法的错误率取平均值，以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试，并获得10次错误率的总和
for k in range(numTests):
errorSum += colicTest()
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为：{:.2%}".format(errorSum/float(numTests)))
输出：
if __name__ == ‘__main__‘:
multiTest()
测试结果的错误率为：29.85%
测试结果的错误率为：32.84%
测试结果的错误率为：35.82%
测试结果的错误率为：40.30%
测试结果的错误率为：34.33%
测试结果的错误率为：46.27%
测试结果的错误率为：32.84%
测试结果的错误率为：37.31%
测试结果的错误率为：29.85%
测试结果的错误率为：50.75%
10次算法测试后平均错误率为：37.01%
小结：
classifyVector(inX, weights)函数，是以最佳回归系数和特征向量作为输入来计算最终对应的Sigmoid值。如果Sigmoid值大于0.5,函数返回1，否则返回0。注意：这个函数后面其他实例也会经常用到，因为这个函数相当于一个分类器，可以获取到最终的预测结果。colicTest()函数，是用于打开测试集和训练测试集，并对数据进行格式化处理的函数，函数最终放回测试的错误率。multiTest()函数，其功能是调用10次colicTest()函数并求结果的平均值。为了使最终错误率更有说服力。从kNN算法里面的小例子得到启发，使用打斗数和接吻数这两个特征最终预测得到的电影类型只有两种：爱情片和动作片。所以符合Logistic回归算法的使用标准。
特征说明：打斗数、接吻数
类型说明：1表示动作片；0表示爱情片
自制数据代码展示：
# !/usr/bin/python3
# -*- coding: utf-8 -*-
# @Time : 2020/4/26 17:21
# @Author : zjw
# @FileName: generateData.py
# @Software: PyCharm
# @Blog ：https://www.cnblogs.com/vanishzeng/
from numpy import *
def generateSomeData(fileName, num):
trainFile = open(fileName, "w")
for i in range(num):
fightCount = float(int(random.uniform(0, 101)))
kissCount = float(int(random.uniform(0, 101)))
if fightCount > kissCount:
label = 1 # 表示动作片
else:
label = 0 # 表示爱情片
trainFile.write(str(fightCount) + "\t" + str(kissCount) + "\t" + str(float(label)) + "\n")
trainFile.close()
if __name__ == ‘__main__‘:
generateSomeData("data/movieTraining.txt", 200)
generateSomeData("data/movieTest.txt", 100)
自制数据思路：通过随机生成打斗数和接吻数（数量在100以内），判断当打斗数大于接吻数时为动作片，记为1；当接吻数大于打斗数时为爱情片，记为0。并将数据写入相应的txt文件中。这里生成了200个训练样本和100个测试样本。最后，还经过对生成的样本数据，进行手动修改几个类别，以达到更加实际现实的样本数据。
样本展示：
movieTraining.txt训练样本展示：
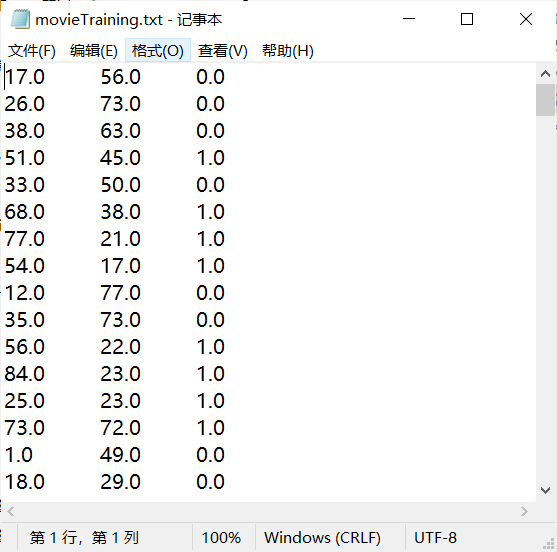
movieTest.txt测试样本展示：
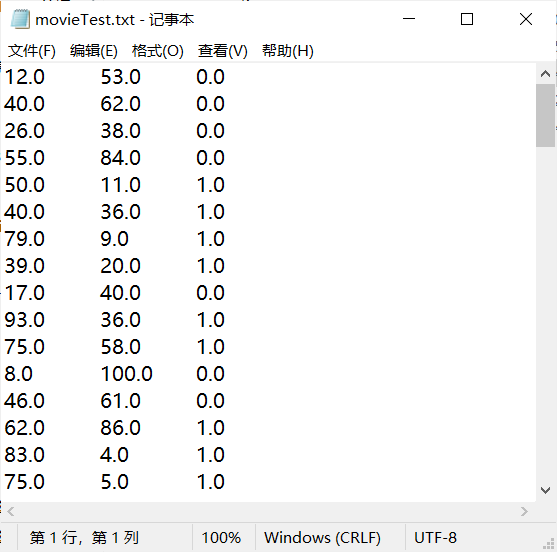
测试算法：使用Logistic回归预测电影类别（关键代码展示）
def classifyVector(inX, weights):
"""
使用梯度上升算法获取到的最优系数来计算测试样本中对应的Sigmoid值。
其中Sigmoid值大于0.5返回1，小于0.5返回0.
:param inX: 特征数组
:param weights: 最优系数
:return: 返回分类结果，即1或0
"""
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def movieTest():
"""
使用Logistic回归算法测试判断电影类别的错误率。
:return: 错误率
"""
trainFile = open("data/movieTraining.txt")
testFile = open("data/movieTest.txt")
trainSet = []
trainLabels = []
for line in trainFile.readlines():
lineArr = line.strip().split(‘\t‘)
trainSet.append([float(lineArr[0]), float(lineArr[1])])
trainLabels.append(float(lineArr[2]))
trainWeights = stocGradAscent1(array(trainSet), trainLabels, 500)
errorCount = 0
allTestCount = 0
for line in testFile.readlines():
allTestCount += 1
lineArr = line.strip().split(‘\t‘)
eigenvalue = [float(lineArr[0]), float(lineArr[1])]
if classifyVector(eigenvalue, trainWeights) != float(lineArr[2]):
errorCount += 1
errorRate = float(errorCount)/float(allTestCount)
print("错误率为：{:.2%}".format(errorRate))
return errorRate
def multiTest():
"""
多次测试算法的错误率取平均值，以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试，并获得10次错误率的总和
for k in range(numTests):
errorSum += movieTest()
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为：{:.2%}".format(errorSum/float(numTests)))
输出：
if __name__ == ‘__main__‘:
multiTest()
错误率为：11.00%
错误率为：6.00%
错误率为：5.00%
错误率为：6.00%
错误率为：5.00%
错误率为：10.00%
错误率为：4.00%
错误率为：7.00%
错误率为：14.00%
错误率为：11.00%
10次算法测试后平均错误率为：7.90%
小结：
在这个例子中我们使用到一批心脏检查样本数据（数据来源于网络：Statlog (Heart) Data Set），这里我将获取到的270个样本数据分成两部分，一部分作为训练样本（heartTraining.txt)有200个样本数据，一部分作为测试样本（heartTest.txt）有70个样本数据。数据各列的特征（有13个特征）和是否为心脏病如下图所示：
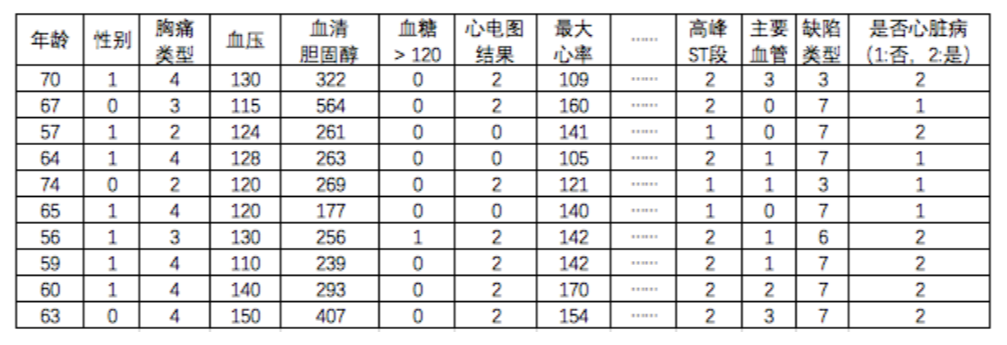
注：这里中间有些特征没有标明，但这并不影响我们对数据的操作。
这里为了使数据便于后面的操作，我将数据集中最后一列数据进行了修改，原来是1表示否，2表示是；修改后1表示是，0表示否。
重构数据集的代码如下：
# !/usr/bin/python3
# -*- coding: utf-8 -*-
# @Time : 2020/4/29 9:54
# @Author : zjw
# @FileName: modifyDataFile.py
# @Software: PyCharm
# @Blog ：https://www.cnblogs.com/vanishzeng/
def modifyData(fileName):
file = open(fileName, ‘r‘)
allStr = []
for line in file.readlines():
arr = line.strip().split(‘ ‘)
if arr[13] == ‘1‘:
arr[13] = ‘0‘
else:
arr[13] = ‘1‘
s = ‘‘
for i in range(14):
s += arr[i] + ‘\t‘
s += ‘\n‘
allStr.append(s)
file.close()
newFile = open(fileName, ‘w‘)
newFile.writelines(allStr)
newFile.close()
if __name__ == ‘__main__‘:
modifyData(‘data/heartTest.txt‘)
modifyData(‘data/heartTraining.txt‘)
重构思路：将文本文件中的数据都读取出来，然后进行切割，将数据中的最后一列中的值通过if判别进行替换。并将修改好后的列表转化为一个个字符串，存入到allStr这个总列表中。最后再以写的方式打开文件，通过writelines()方法一次性将allStr列表写入文件中。
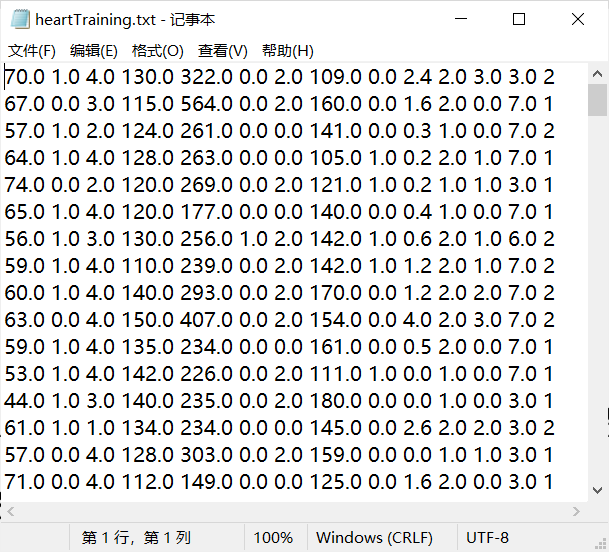
重构后的文件数据集：
训练样本（heartTraining.txt）：
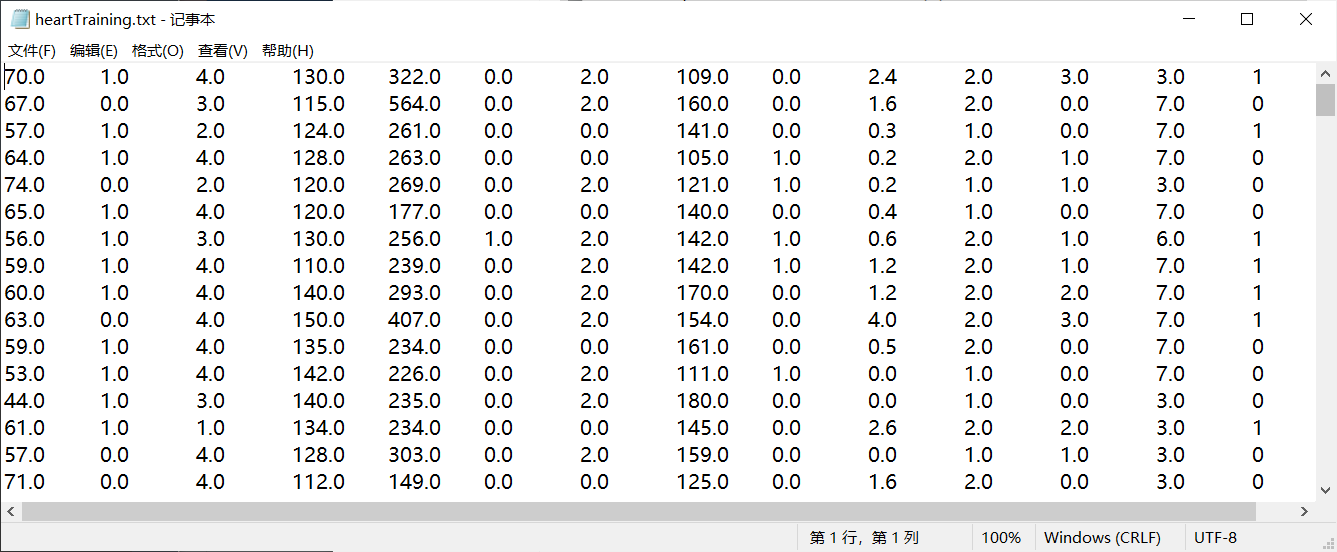
测试样本（heartTest.txt）：
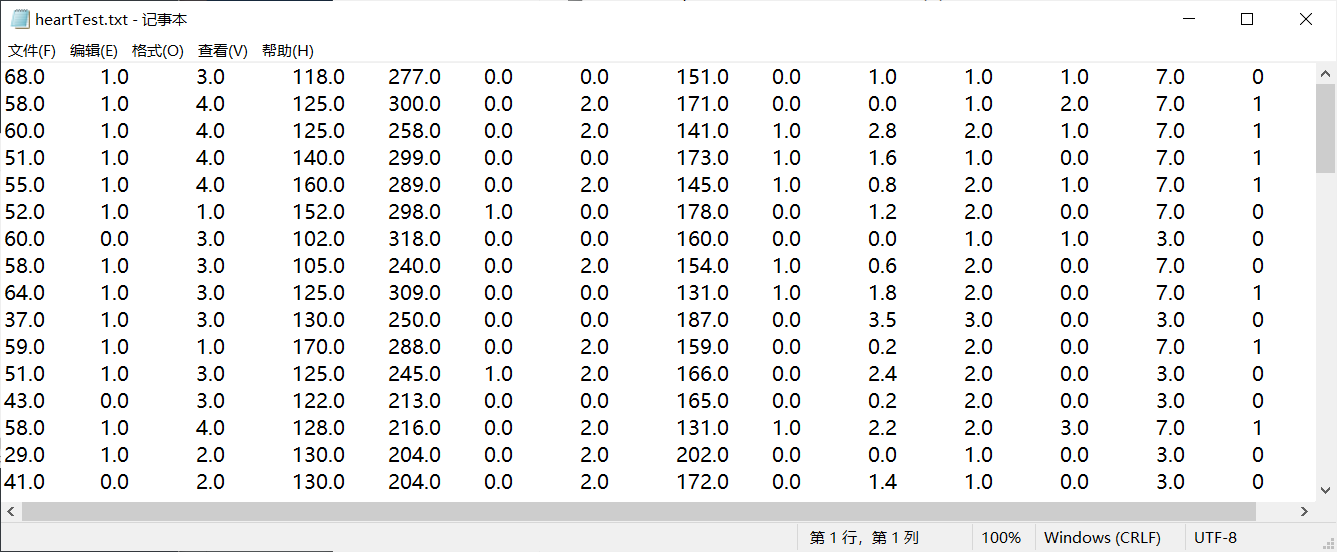
测试算法：使用Logistic回归预测是否为心脏病（关键代码展示）
def classifyVector(inX, weights):
"""
使用梯度上升算法获取到的最优系数来计算测试样本中对应的Sigmoid值。
其中Sigmoid值大于0.5返回1，小于0.5返回0.
:param inX: 特征数组
:param weights: 最优系数
:return: 返回分类结果，即1或0
"""
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def heartTest():
"""
使用Logistic回归算法诊断心脏病的错误率。
:return:错误率
"""
trainFile = open("data/heartTraining.txt")
testFile = open("data/heartTest.txt")
trainSet = []
trainLabels = []
for line in trainFile.readlines():
lineArr = line.strip().split(‘ ‘)
temArr = []
for i in range(13):
temArr.append(float(lineArr[i]))
trainSet.append(temArr)
trainLabels.append(float(lineArr[13]))
trainWeights = stocGradAscent1(array(trainSet), trainLabels, 100)
errorCount = 0
allTestCount = 0
for line in testFile.readlines():
allTestCount += 1
lineArr = line.strip().split(‘ ‘)
eigenvalue = []
for i in range(13):
eigenvalue.append(float(lineArr[i]))
if classifyVector(eigenvalue, trainWeights) != float(lineArr[13]):
errorCount += 1
errorRate = float(errorCount) / float(allTestCount)
print("错误率为：{:.2%}".format(errorRate))
return errorRate
def multiTest():
"""
多次测试算法的错误率取平均值，以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试，并获得10次错误率的总和
for k in range(numTests):
errorSum += heartTest()
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为：{:.2%}".format(errorSum/float(numTests)))
输出：
if __name__ == ‘__main__‘:
multiTest()
错误率为：18.57%
错误率为：17.14%
错误率为：15.71%
错误率为：31.43%
错误率为：24.29%
错误率为：12.86%
错误率为：21.43%
错误率为：12.86%
错误率为：32.86%
错误率为：22.86%
10次算法测试后平均错误率为：21.00%
小结：
改进函数展示：
def dataTest(trainFileName, testFileName, numOfFeatures):
"""
函数功能：测试回归算法预测数据样本的错误率。
函数伪代码：
1. 读取训练样本中的数据，进行格式化处理；
2. 将格式化处理后的数据传入随机梯度上升算法函数中，获取到最佳参数。
3. 再读取测试样本中的数据，进行格式化处理后，调用分类器函数（传入样本特征和最佳参数），可以预测出最终特征。与测试数据中的实际特征进行比较，计算出错误次数。
4. 最终通过错误次数/测试样本总数**求出错误率。
:param trainFileName: 训练样本的文件路径/文件名
:param testFileName: 测试样本的文件路径/文件名
:param numOfFeatures: 样本所包含的特征数量
:return:
"""
trainFile = open(trainFileName)
testFile = open(testFileName)
trainSet = []
trainLabels = []
for line in trainFile.readlines():
lineArr = line.strip().split(‘\t‘)
temArr = []
for i in range(numOfFeatures):
temArr.append(float(lineArr[i]))
trainSet.append(temArr)
trainLabels.append(float(lineArr[numOfFeatures]))
trainWeights = stocGradAscent1(array(trainSet), trainLabels, 200)
errorCount = 0
allTestCount = 0
for line in testFile.readlines():
allTestCount += 1
lineArr = line.strip().split(‘\t‘)
eigenvalue = []
for i in range(numOfFeatures):
eigenvalue.append(float(lineArr[i]))
if classifyVector(eigenvalue, trainWeights) != float(lineArr[numOfFeatures]):
errorCount += 1
errorRate = float(errorCount) / float(allTestCount)
print("错误率为：{:.2%}".format(errorRate))
return errorRate
def multiTest1(trainFileName, testFileName, numOfFeatures):
"""
多次测试算法的错误率取平均值，以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试，并获得10次错误率的总和
for k in range(numTests):
errorSum += dataTest(trainFileName, testFileName, numOfFeatures)
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为：{:.2%}".format(errorSum/float(numTests)))
输出：
if __name__ == ‘__main__‘:
print("示例1：示例1：从疝气病症预测病马的死亡率")
multiTest1(‘data/horseColicTraining.txt‘, ‘data/horseColicTest.txt‘, 21)
print("\n示例2：从打斗数和接吻数预测电影类型")
multiTest1(‘data/movieTraining.txt‘, ‘data/movieTest.txt‘, 2)
print("\n示例3：从心脏检查样本帮助诊断心脏病")
multiTest1(‘data/heartTraining.txt‘, ‘data/heartTest.txt‘, 13)
示例1：从疝气病症预测病马的死亡率
错误率为：32.84%
错误率为：29.85%
错误率为：29.85%
错误率为：37.31%
错误率为：29.85%
错误率为：34.33%
错误率为：31.34%
错误率为：29.85%
错误率为：29.85%
错误率为：31.34%
10次算法测试后平均错误率为：31.64%示例2：从打斗数和接吻数预测电影类型
错误率为：14.00%
错误率为：6.00%
错误率为：14.00%
错误率为：3.00%
错误率为：6.00%
错误率为：11.00%
错误率为：5.00%
错误率为：11.00%
错误率为：5.00%
错误率为：5.00%
10次算法测试后平均错误率为：8.00%示例3：从心脏检查样本帮助诊断心脏病
错误率为：20.00%
错误率为：22.86%
错误率为：17.14%
错误率为：22.86%
错误率为：18.57%
错误率为：18.57%
错误率为：35.71%
错误率为：22.86%
错误率为：35.71%
错误率为：18.57%
10次算法测试后平均错误率为：23.29%
小结：
dataTest(trainFileName, testFileName, numOfFeatures)这个函数，增加了三个参数的目的是，原来三个函数中的不同的地方就是不同的文件和不同的特征数量，所以以参数的形式传递进来，即使有所不同，但是以函数内参数形式调用即可实现相同的功能。multiTest1(trainFileName, testFileName, numOfFeatures)这个函数，也是增加了和上面同样的三个参数，主要是因为在这个函数中要调用dataTest()这个函数，所以需要需要通过multiTest1这个函数间接帮忙传递参数。Logistic回归算法的目的是寻找一个非线性函数Sigmoid的最佳拟合参数，求解过程可以使用最优化算法来完成。
最优化算法中，最常用的是梯度上升算法。梯度上升算法可以简化为效率比较高的随机梯度上升算法。
改进后的随机梯度上升算法的效果和梯度上升算法效果相当，但是占用更少的计算资源且效率更高。
Sigmoid函数：
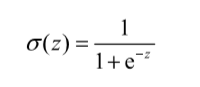
函数封装很重要，可以解决代码冗余问题，此外也可以提高开发效率，不必每次一有新数据，就要重新写新的函数来满足要求。好的代码封装，后续只要调用相应的函数就可以完成指定的目标。
numpy相关函数:
版权声明：欢迎转载=>请标注信息来源于 Vanish丶博客园
[机器学习实战-Logistic回归]使用Logistic回归预测各种实例
标签：lis 加载 alt ade 作者 close 相对 文本文件 pychar
原文地址：https://www.cnblogs.com/vanishzeng/p/12803538.html
