Tarjan 复习

标签：一个   蓝色   http   优先   时间戳   最小   oss   for   原来   

1.dfs 树

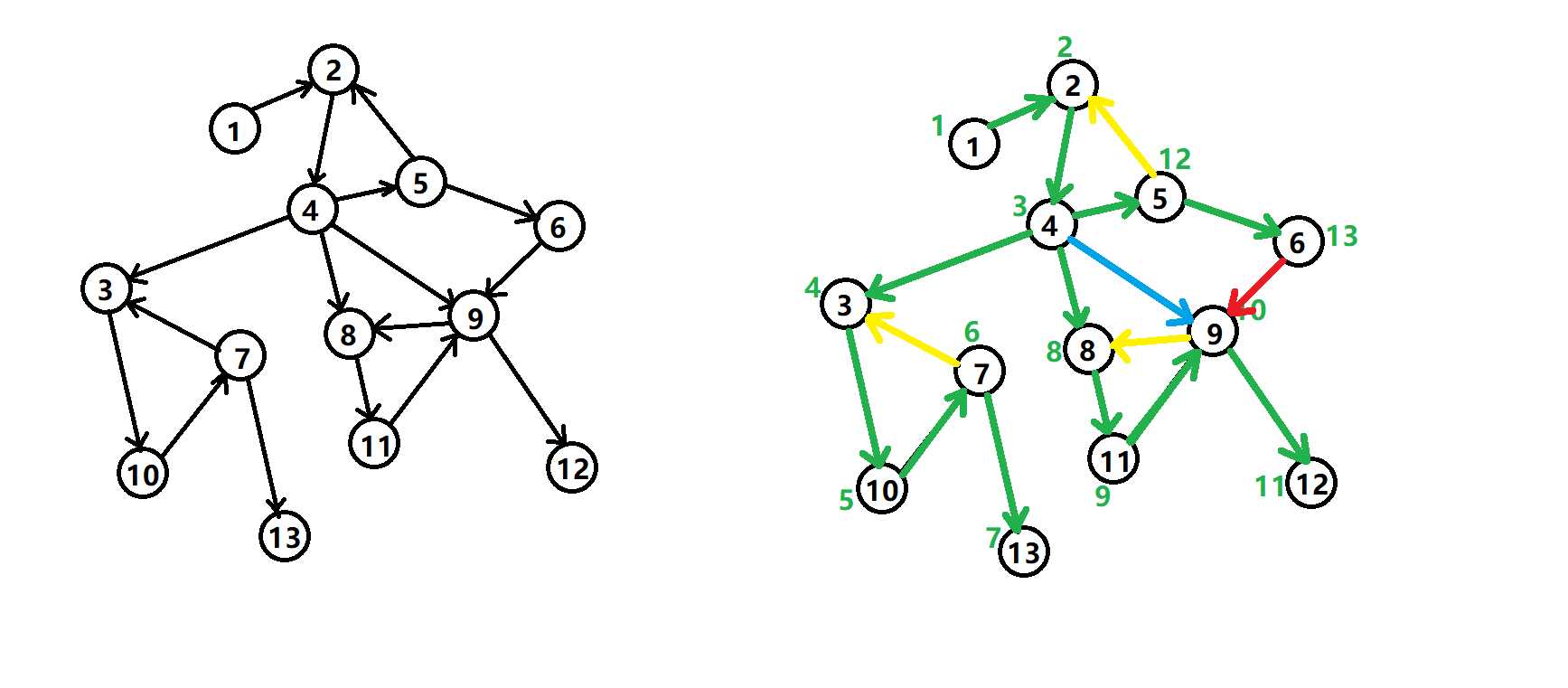
• 上图右图是左图以1为起点进行DFS时产生的生成树。
• 有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：
  1. 树边(tree edge)：绿色边，每次搜索找到一个还没有访问过的结点（白点）的时候就形成了一条树边。
  2. 返祖边(back edge)：黄色边，也被叫做回边，即指向祖先结点（灰点）的边。
  3. 横叉边(cross edge)：红色边，它主要是在搜索的时候遇到了一个已经访问过（黑点dfn[u]>dfn[v]）的结点，但是这个结点 并不是 当前结点的祖先时形成的。
  4. 前向边(forward edge)：蓝色边，它是在搜索的时候遇到子树中的结点（黑点`dfn[u]）的时候形成的。
• 无向图不存在横叉边和前向边。

2.强连通分量

即任意两点间都可达.(实际上为一个环)

Tarjan基于对图的深度优先搜索，并对每个节点引入两个值：

• dfn[u]：节点u的时间戳，记录点u是DFS过程中第几个访问的节点。
• low[u]：记录节点u或u的子树不经过搜索树上的边(树边)能够到达的时间戳最小的节点。
• 初始时，dfn[u]==low[u]
• 对于每一条与u相连的边<u,v>：
  • 若在搜索树上v是u的子节点，即边<u,v>是树枝边，则更新low[u]= min(low[u], low[v])；
  • 若 <u,v> 不是搜索树上的边 (即这条边为反祖边)， 则更新low[u]= min(low[u], dfn[v])；

3.缩点

即把每个环(强连通分量)缩成一个点, 因为在环中任意两点间可达, 所以缩成点后和原来是等效的, 缩点后的点权为环中点权之和. 进行缩点后, 我们可以得到DAG图(或者树), 从而使问题容易解决

Tarjan 复习

标签：一个   蓝色   http   优先   时间戳   最小   oss   for   原来   

原文地址：https://www.cnblogs.com/hzoi-poozhai/p/12804911.html