标签:log lse 顶点 img const info 生成树 int class
假如一堵墙上有一些钉子,这些钉子由许多细线连接起来,当我们试图去掉其他线,只留下较短的线使图钉连接起来,这就形成了最小生成树。
最小生成树正式描述是:给定无方向带权图G=(V,E),最小生成树集合为T,T为最小代价连接V中所有顶点所用边E的最小集合。
最小生成树常用Prim算法和Dijkstra算法求得,二者都建立在贪心基础上。还有一种是Kruskal算法,对权重排序并得出答案,较好理解。
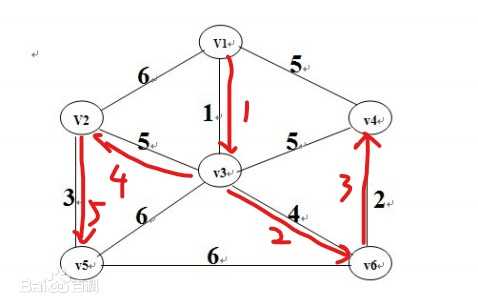
Prim算法:
Prim即从任意已连接顶点开始,每次选一个与当前顶点连边最短的点,将两者的连边加入树集合中。在搜索与当前顶点最近点时用的贪心算法,不过贪心算法一般只是较优解,而Prim提供的往往是最优解。
#include<stdio.h> #define MAX 0x7FFF7FFF typedef struct T { int cost; int mst; int flag; }Tree; Tree tree[100]; int graph[100][100]; void prim(int head,int number) { int i,j,min,mind; for(i=1;i<=number;i++) { tree[i].cost=graph[head][i];//开头到各点距离 tree[i].flag=0; tree[i].mst=head; } tree[head].flag=1; for(i=1;i<number;i++) { min=MAX; for(j=1;j<=number;j++) { if(tree[j].cost<min&&tree[j].flag==0) { min=tree[j].cost; mind=j; } } tree[mind].flag=1; for(j=1;j<=number;j++) { if((tree[j].cost>graph[mind][j])&&tree[j].flag==0)//更新已连接顶点与未连接顶点最短距离 { tree[j].cost=graph[mind][j]; tree[j].mst=mind; } } } } int main() { int n,num;//n为个数,num为例子个数 int s,d,a,cost,b; scanf("%d %d",&n,&num); for(a=1;a<=n;a++) { for(b=1;b<=n;b++) graph[a][b]=MAX;//初始化图 } for(a=0;a<num;a++) { scanf("%d %d %d",&s,&d,&cost); graph[s][d]=cost; graph[d][s]=cost; } prim(1,n); for(a=2;a<=n;a++) printf("%d->%d,cost:%d\n",tree[a].mst,a,tree[a].cost); }
Kruskal算法
kruskal算法是对权重排序后进行判断循环,感觉也比较简便。复杂度为O(E|log|E||)【E为无向图边数】,因此不适用运行大量数据。
#include<stdio.h> #include<string.h> #include<stdlib.h> const long int M=1000001; struct R{int A;int B;int length;}tree[10005]; int cmp(const void* a,const void *b) { return (*(R*)a).length-(*(R*)b).length; } int main() { int n,m,sum,b,c; int sign[105]={0};//标志对应顶点是否已加入树中 scanf("%d %d",&n,&m); { for(b=0,sum=0;b<m;b++) scanf("%d %d %d",&tree[b].A,&tree[b].B,&tree[b].length); qsort(tree,b,sizeof(tree[0]),cmp);//依权重由小到大排序 sign[1]=1; for(b=1;b<n;b++) { for(c=0;c<n;c++) if(sign[tree[c].A]+sign[tree[c].B]==1) { if(sign[tree[c].A]==1) printf("%d->%d,cost:%d\n",tree[c].A,tree[c].B,tree[c].length); else printf("%d->%d,cost:%d\n",tree[c].B,tree[c].A,tree[c].length); sign[tree[c].A]=1; sign[tree[c].B]=1; break; } } } }
标签:log lse 顶点 img const info 生成树 int class
原文地址:https://www.cnblogs.com/xntxdy/p/12776229.html