标签：cst   red   semi   with   包括   假设   one   before   href   

题目

Although Inzane successfully found his beloved bone, Zane, his owner, has yet to return. To search for Zane, he would need a lot of money, of which he sadly has none. To deal with the problem, he has decided to hack the banks.

There are n banks, numbered from 1 to n. There are also n?-?1 wires connecting the banks. All banks are initially online. Each bank also has its initial strength: bank i has initial strength a i.

Let us define some keywords before we proceed. Bank i and bank j are neighboring if and only if there exists a wire directly connecting them. Bank i and bank j are semi-neighboring if and only if there exists an online bank k such that bank i and bank k are neighboring and bank k and bank j are neighboring.

When a bank is hacked, it becomes offline (and no longer online), and other banks that are neighboring or semi-neighboring to it have their strengths increased by 1.

To start his plan, Inzane will choose a bank to hack first. Indeed, the strength of such bank must not exceed the strength of his computer. After this, he will repeatedly choose some bank to hack next until all the banks are hacked, but he can continue to hack bank x if and only if all these conditions are met:

1. Bank x is online. That is, bank x is not hacked yet.
2. Bank x is neighboring to some offline bank.
3. The strength of bank x is less than or equal to the strength of Inzane‘s computer.

Determine the minimum strength of the computer Inzane needs to hack all the banks.

Input

The first line contains one integer \(n (1?≤?n?≤?3·10^5)\) — the total number of banks.

The second line contains n integers \(a_1,?a_2,?...,?a_n (?-?10^9?≤?a_i?≤?10^9)\) — the strengths of the banks.

Each of the next n?-?1 lines contains two integers \(u_i\) and \(v_i\) \((1?≤?u_i,?v_i?≤?n, u_i?≠?v_i)\) — meaning that there is a wire directly connecting banks u i and v i.

It is guaranteed that the wires connect the banks in such a way that Inzane can somehow hack all the banks using a computer with appropriate strength.

Output

Print one integer — the minimum strength of the computer Inzane needs to accomplish the goal.
　

Examples

Input 1

5
1 2 3 4 5
1 2
2 3
3 4
4 5

Output 1

5

Input 2

7
38 -29 87 93 39 28 -55
1 2
2 5
3 2
2 4
1 7
7 6

Output 3

93

Input 3

5
1 2 7 6 7
1 5
5 3
3 4
2 4

Output 3

8

Note

In the first sample, Inzane can hack all banks using a computer with strength 5. Here is how:

• Initially, strengths of the banks are [1,?2,?3,?4,?5].
• He hacks bank 5, then strengths of the banks become [1,?2,?4,?5,??-?].
• He hacks bank 4, then strengths of the banks become [1,?3,?5,??-?,??-?].
• He hacks bank 3, then strengths of the banks become [2,?4,??-?,??-?,??-?].
• He hacks bank 2, then strengths of the banks become [3,??-?,??-?,??-?,??-?].
• He completes his goal by hacking bank 1.
  In the second sample, Inzane can hack banks 4, 2, 3, 1, 5, 7, and 6, in this order. This way, he can hack all banks using a computer with strength 93.

题解

解题思路

这道题就是一颗树，删去一个点后连着的点以及相连的点的相连的点的权值+1
假设第一个选了1号节点，那么节点权值的改变如下图所示

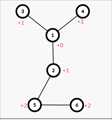
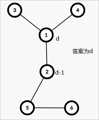
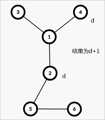
就可以转化为，指点一个点，与这个点相连的点权值+1，其他点权值+2，使整棵树权值最大的点最小

找到最大值d，那结果就只可能是d, d+1, d+2。

• 对于结果为d的情况，就是只有一个权值为d的点而且除了这个点以及和这个点相连的点，其他的点权值不为d-1
  
• 对于结果为d+1的情况，就是有一个点，与之相连的点，包括自己，包含了所有权值为d的点
  
• 其余的情况都为d+2

代码

#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 3e5+5;
struct side {
    int t, next;
}e[N*2];
int head[N], tot;
void add(int x, int y) {
    e[++tot].next = head[x];
    head[x] = tot;
    e[tot].t = y;
}
int n, a[N], d = (int)-2e9, d1, d2, h;
//初始化一定要注意
int sum(int x, int num) {
    int s = a[x] == num ? 1 : 0;
    for(int i = head[x]; i; i = e[i].next)
        if (a[e[i].t] == num) s++;
    return s;
}//sum函数求x连接的点权值为num的数量（包括自己）
int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]), d = max(d, a[i]);
    for(int i = 1; i <= n; i++) {
        if (a[i] == d) d1++, h = i;
        else if (a[i] == d - 1) d2++;
    }
    for(int i = 1, x, y; i < n; i++) {
        scanf("%d%d", &x, &y);
        add(x, y); add(y, x);
    }
    if (d1 == 1 & sum(h, d - 1) == d2) 
        return printf("%d", d), 0;
    for(int i = 1; i <= n; i++)
        if (sum(i, d) == d1)
            return printf("%d", d + 1), 0;
    return printf("%d", d + 2), 0;
}

真的是太难调了

2E Bank Hacking——思维题

标签：cst   red   semi   with   包括   假设   one   before   href   

原文地址：https://www.cnblogs.com/Z8875/p/12805656.html