标签：简单 比较 拓扑 ima 注意 key 缓冲 数量级 oct
明确滤波器设计目标，
例将10Khz 的方波得到10kHz的正弦波，通过示波器的傅里叶分析，可以知道方波主要有方波频率 的奇次谐波构成，，可以简化为衰减30KHz 的谐波。
最简单的体统滤波器就是RC滤波，和分压器类似，只是将下侧电阻换成了电容，由于电容的阻抗和频率相关，低频时，电容看起来就是开路，频率慢慢升高后电容开始接近短路，输出电压也会越来越低。
假设要在30KHz时使信号衰减50dB，
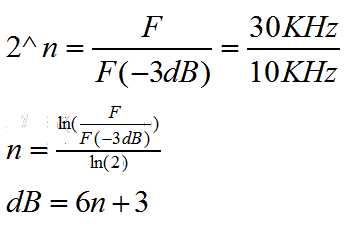，由此得到我们需要所衰减的频率就可以有右式得出。其中n为倍频程数。
当n=2时，频率应该是40kHz,衰减的分贝数为15dB，也就是说，即使在40KHz时，也仅仅是衰减了15dB,不可以达到要求的50dB。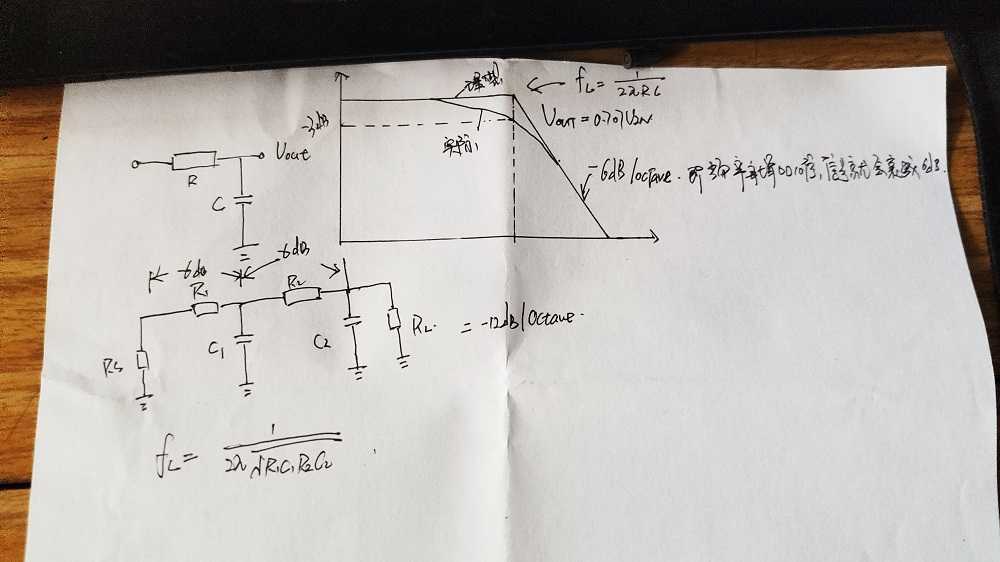
所以，通过增加滤波器的数量，来达到，例如将连个RC滤波器级联，得到12dB/octave的波形。
注意：当级联滤波器时，尤其要注意的是每一级的源和负载的阻抗。
所以，源的阻抗Rs要求较低，因为串联起来时会影响后级，如果源的阻抗较大会影响滤波的特性。
同样，这里要求负载的阻抗要较大，这样前面的滤波器阻抗的影响会尽可能的小，显然，这里负载和C2电容并联，如果负载很小的话C2也会分走一些电流。
第一级滤波器，将第二级滤波器和负载电阻都看作负载，所以第二级的滤波器的输入电阻要比第一级滤波器的输出电阻要大不少，所以R2要比R1大一个数量级来避免被分压分太多，通常来说，这种滤波器不会见到太多 级，一般不会超过两个。因为级联过多导致这些电阻变得非常大，设计的截止频率不变，电容C就要设计的非常小。
这样，有源滤波器的好处就体现出来了。我们在每一级将都加入一个缓冲放大器，他提供的输入阻抗与前级相比较较高，输出阻抗相对较低。
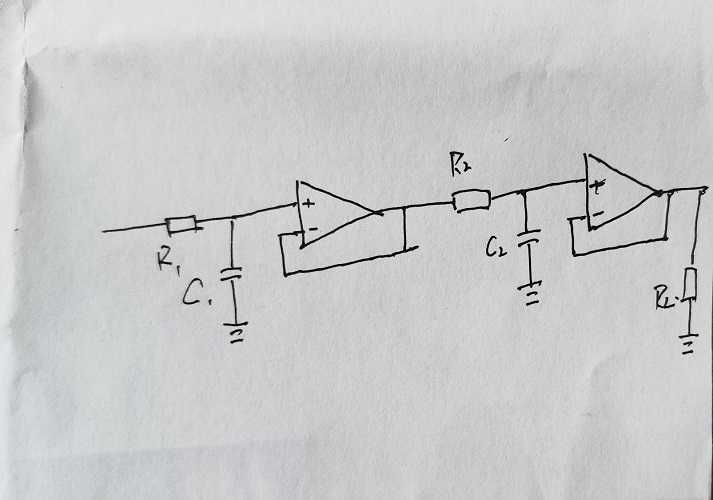
但是，这样使用放大器很不划算，
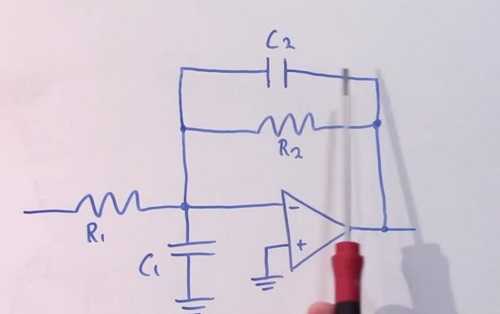
当频率很低时，C2的阻抗很大，相当于断路，有增益R2/R1，当频率变高时，增益渐渐变为1，也实现了-12dB/octave的衰减，
Sallen-Key
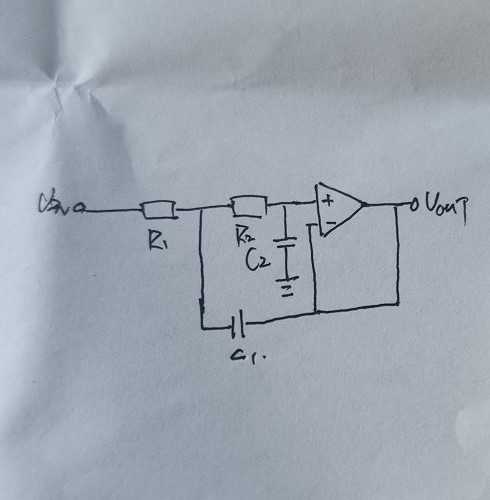
R2和C2组成了一个简单 的RC滤波器，然后接上运放的同相端，此时增益为1， 低频时，电容的阻抗相当大，相当于断路，高频时，电容阻抗小，相当于短路，由此R1，C1，R2，C2构成二阶滤波器，形成-12dB/octave的衰减。同时，在某些频率下，当C1的阻抗小时，形成正反馈，使得增益会大于1，同时，通过改变不同的C1，使得C1阻抗减小，就会的得到更大的增益。
标签：简单 比较 拓扑 ima 注意 key 缓冲 数量级 oct
原文地址：https://www.cnblogs.com/--Destroyer--/p/12811790.html
