标签:其他 出现 nbsp 去掉 通过 strong 它的 节点 定义
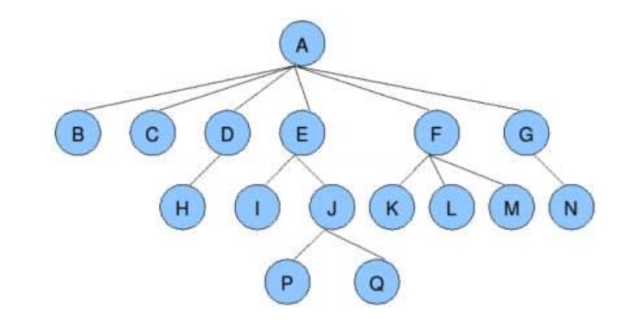
树是一种数据结构.
树是一种可以递归定义的数据结构.
树由n个节点组成的集合
n=0时,是空树
n>0,一个节点作为根节点,其他节点可以分为m个集合,每个集合本身又是一棵树(这就是重复单元)
树的度:整个树中最大的节点的度就是树的度
节点的度:就是一个节点的子节点有多少个
父节点:在上面紧挨着它的节点就是父节点(A是D的父节点,但是A不是H的父节点)
子节点:一个节点下面紧挨着它的节点就是它的子节点(A下面的B,C,D,E,F,G都是它的子节点)
根节点(上面没有父节点):A
叶子节点(后面不能再分叉):B,C,H,I,P,Q,K,L,M,N,或者说度为0的节点就叫叶子节点
树的深度(高度):根到叶子最长的节点个数(就是最多几层)
子树:EIJPQ就是个子树
度不超过2的树(整个树中每个节点最多有连个孩子节点,分别为左孩子节点和右孩子节点)就是二叉树
一个二叉树,如果每一层的节点数都达到最大值,则这个二叉树就是满二叉树.
如图:
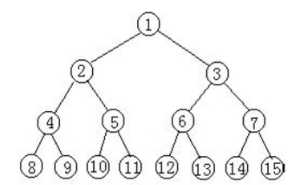
叶子节点只能出现在最下层和次下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树
如图:
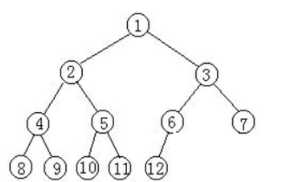
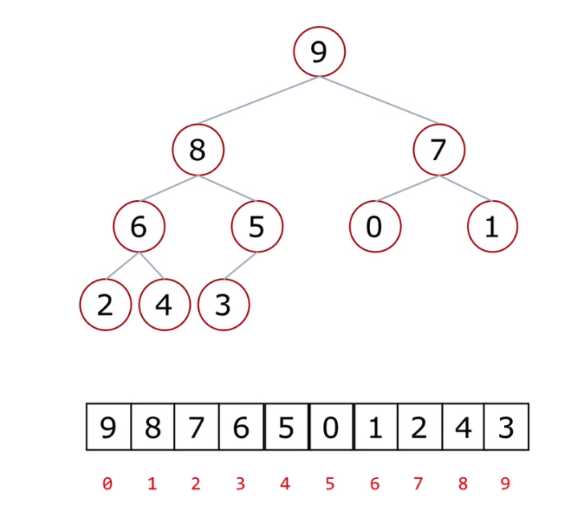
节点的索引下标用红字写在上面了
看一下父节点(假设是i)的下标与左右孩子结点的关系
所有左节点的下标都是2i+1(可以试i=0,1,2,3得到的索引全是左下标)
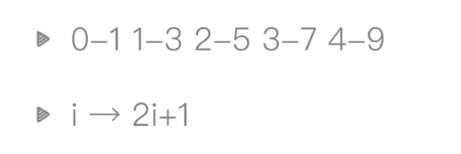
所有右节点的下标都是2i+2

只要知道父节点就可以算出左和右的子节点
知道到左右节点的索引后都可以直接减一再底板除(//)来得到父节点的索引(底板除得到小数后向下取整,不会四舍五入)
一种特殊的完全二叉树结构
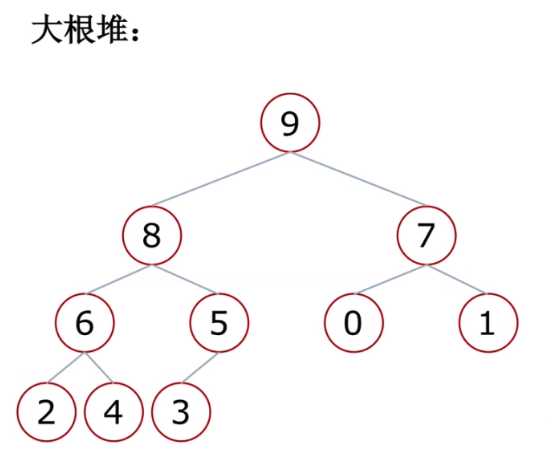
大根堆:
一棵完全二叉树,满足任一节点都比孩子节点大
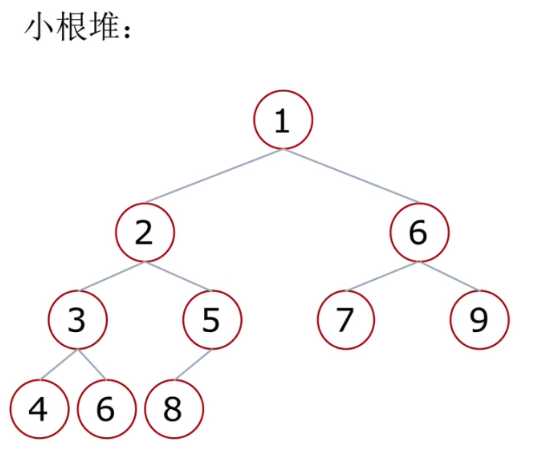
小根堆:
一棵完全二叉树,满足任一节点都比其孩子节点小
堆整体不是个跟堆,但是左子树是个大根堆或小根堆,右子树是个大根堆或者小根堆(左右要保持一致都是大根堆或者都是小根堆)
这时可以通过向下调整使得整个跟堆变成一个大根堆或者小根堆
如图,左右都是大根堆,但是整体不是大根堆,此时要把2向下调整
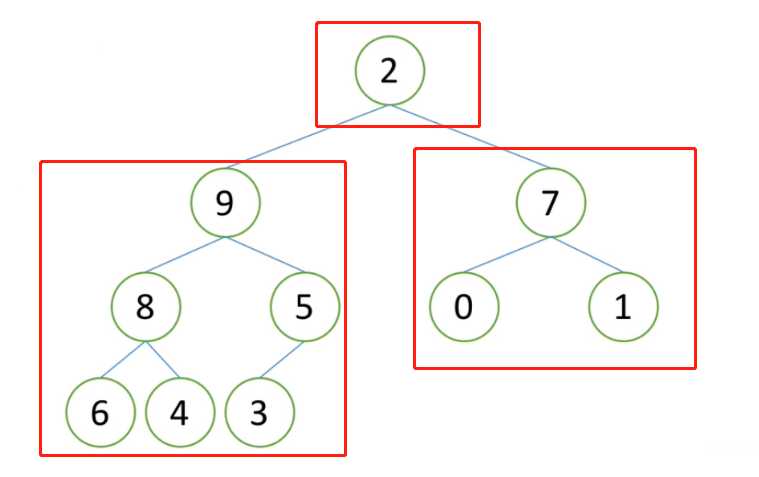
调整后:整体是个大根堆
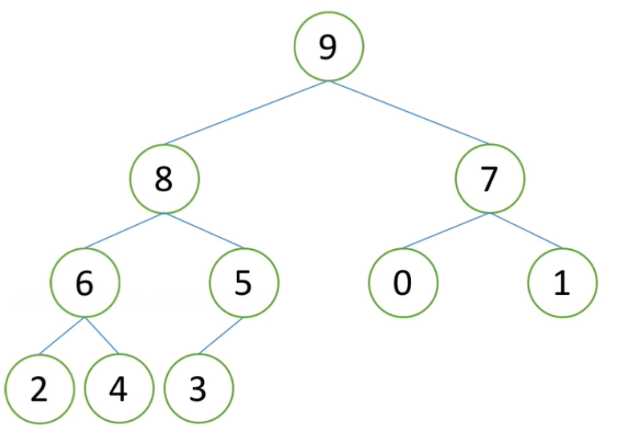
步骤:
1.建立堆
2.得到堆顶元素,为最大元素
3.去掉堆顶,将堆最后一个元素(叶子结点最右边的元素,上图中3就是最后一个元素)放到堆顶,此时可以通过一次调整(向下调整)重新使堆有序
4.堆顶元素为第二大元素
5.重复步骤3,直到堆为空
标签:其他 出现 nbsp 去掉 通过 strong 它的 节点 定义
原文地址:https://www.cnblogs.com/shengjunqiye/p/12813177.html