标签:arrays alt 完全 需要 img pre 最大 return out
/*
Serling公司购买长钢条,将其切割为短钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。
假定我们知道Serling公司出售一段长为i英寸的钢条的价格为pi(i=1,2,…,单位为美元)。钢条的长度均为整英寸。
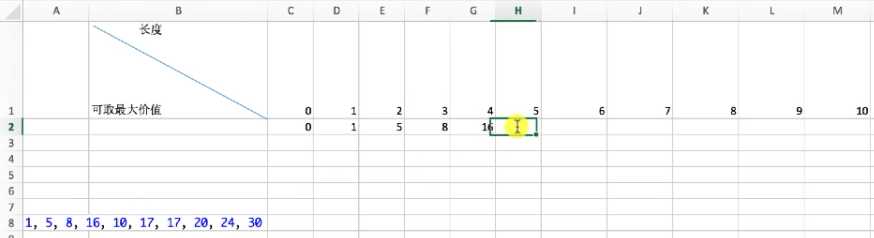
| 长度i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| - | - | - | - | - | - | - | - | - | - |
价格pi | 1 | 5 | 8 | 16 | 10 | 17 | 17 | 20 | 24 | 30 |
钢条切割问题是这样的:给定一段长度为n英寸的钢条和一个价格表pi(i=1,2,…n),求切割钢条方案,使得销售收益rn最大。
注意,如果长度为n英寸的钢条的价格pn足够大,最优解可能就是完全不需要切割。
*/

1 import java.util.Arrays; 2 3 public class Eight_13动态规划例题_钢条切割 { 4 static int n = 10; 5 static int[] p = {1,5,8,16,10,17,17,20,24,30}; 6 7 //递归 8 private static int r(int x){ 9 if(x == 0) 10 return 0; 11 12 int ans = 0; 13 for(int i = 1; i <=x; i++){ 14 int v = p[i-1] + r(x-i); 15 ans = Math.max(ans, v); 16 } 17 return ans; 18 } 19 20 //记忆化递归 21 static int[] vs = new int[n+1]; 22 private static int r2(int x){ 23 if(x == 0) 24 return 0; 25 26 int ans = 0; 27 for(int i = 1; i <=x; i++){ 28 if(vs[x-i] == -1){ 29 vs[x-i] = r2(x-i); 30 } 31 int v = p[i-1] + vs[x-i]; 32 ans = Math.max(ans, v); 33 } 34 vs[x] = ans; 35 return ans; 36 } 37 38 //dp解法 39 private static int dp(){ 40 vs[0] = 0; 41 for(int i = 1; i <= n; i++){ //拥有的钢条长度 42 for(int j = 1; j <= i; j++){ //保留j为整段 43 vs[i] = Math.max(p[j-1]+vs[i-j], vs[i]); 44 } 45 } 46 return vs[n]; 47 } 48 public static void main(String[] args) { 49 System.out.println(r(10)); 50 Arrays.fill(vs, -1); 51 System.out.println(r2(10)); 52 System.out.println(dp()); 53 } 54 } 55
标签:arrays alt 完全 需要 img pre 最大 return out
原文地址:https://www.cnblogs.com/z1110/p/12817791.html