标签:ast 常用 利用 nbsp 概率 function error 训练 实际应用
损失函数(loss function)是用来估量你模型的预测值f(x)与真实值Y的不一致程度,衡量模型预测的好坏。它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。
损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下式子
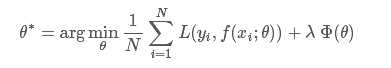
其中,前面的均值函数表示的是经验风险函数,L代表的是损失函数,后面的Φ是正则化项(regularizer)或者叫惩罚项(penalty term),它可以是L1,也可以是L2,或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的θ值。
下面主要列出几种常见的损失函数。
一、log对数损失函数(逻辑回归):
log损失函数的标准形式:
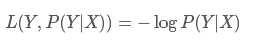
在逻辑回归的推导中,它假设样本服从伯努利分布(0-1分布),然后求得满足该分布的似然函数,接着取对数求极值
把极大化当做是一种思想,进而推导出它的经验风险函数为:最小化负的似然函数。从损失函数的视角来看,它就成了log损失函数
取对数是为了方便计算极大似然估计,因为在MLE中,直接求导比较困难,所以通常都是先取对数再求导找极值点。损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下,使概率P(Y|X)达到最大值(换言之,就是利用已知的样本分布,找到最有可能(即最大概率)导致这种分布的参数值;或者说什么样的参数才能使我们观测到目前这组数据的概率最大)。因为log函数是单调递增的,所以logP(Y|X)也会达到最大值
因此在前面加上负号之后,就等价于最小化损失函数了
二、平方损失函数(最小二乘法, Ordinary Least Squares )
最小二乘的基本原则是:最优拟合直线应该是使各点到回归直线的距离和最小的直线,即平方和最小。
换言之,OLS是基于距离的,而这个距离就是我们用的最多的欧几里得距离
为什么它会选择使用欧式距离作为误差度量呢(即Mean squared error, MSE),主要有以下几个原因:
* 简单,计算方便;
* 欧氏距离是一种很好的相似性度量标准;
* 在不同的表示域变换后特征性质不变。
平方损失(Square loss)的标准形式如下: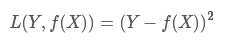
当样本个数为n时,此时的损失函数变为:
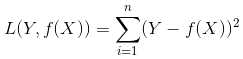
Y-f(X)表示的是残差,整个式子表示的是残差的平方和,而我们的目的就是最小化这个目标函数值(注:该式子未加入正则项),也就是最小化残差的平方和(residual sum of squares,RSS)。
而在实际应用中,通常会使用均方差(MSE)作为一项衡量指标,公式如下:
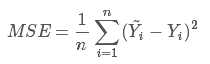
三、指数损失函数(Adaboost)
常用在Adaboost之中
在Adaboost中,经过m此迭代之后,可以得到fm(x):
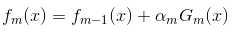
Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数α 和G:
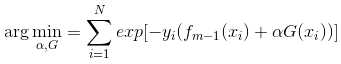
而指数损失函数(exp-loss)的标准形式如下
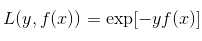
可以看出,Adaboost的目标式子就是指数损失,在给定n个样本的情况下,Adaboost的损失函数为:
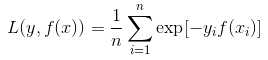
四、Hinge损失函数(SVM)
Hinge 损失函数的标准形式:
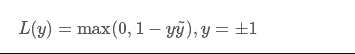
y^为预测值,在-1到1之间,y为目标值(-1或1)。
五、其它损失函数
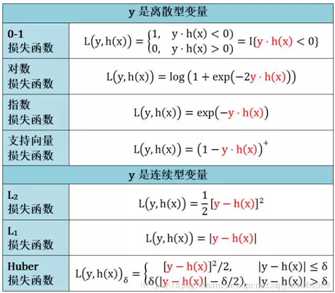
除了以上这几种损失函数,常用的还有:0-1损失是指,预测值和目标值不相等为1,否则为0:
0-1损失函数:(注意是不相等时为1,相等时为0)
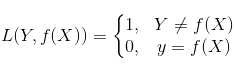
绝对值损失函数:
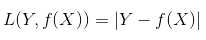
参数越多,模型越复杂,而越复杂的模型越容易过拟合。过拟合就是说模型在训练数据上的效果远远好于在测试集上的性能。此时可以考虑正则化,来权衡损失函数和正则项,减小参数规模,达到模型简化的目的,从而使模型具有更好的泛化能力。
机器学习中的目标函数、损失函数、代价函数有什么区别?
损失函数和代价函数是同一个东西,目标函数是一个与他们相关但更广的概念,对于目标函数来说在有约束条件下的最小化就是损失函数(loss function)。

上面三个图的函数依次为 f1(x) ,f2(x) ,f3(x) 。我们是想用这三个函数分别来拟合Price,Price的真实值记为 Y 。
我们给定 x,这三个函数都会输出一个f(x) ,这个输出的 f(x) 与真实值 y 可能是相同的,也可能是不同的,为了表示我们拟合的好坏,我们就用一个函数来度量拟合的程度,比如: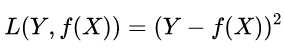
这个函数就称为损失函数(loss function),或者叫代价函数(cost function)。损失函数越小,就代表模型拟合的越好。
那是不是我们的目标就只是让 loss function 越小越好呢?
答案是否定的。
f(x) 关于训练集的平均损失称作经验风险(empirical risk),即
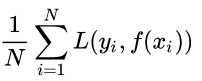
所以我们的目标就是最小化
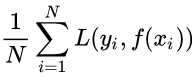
称为经验风险最小化。
如果到这一步就完了的话,那我们看上面的图,那肯定是最右面的 f3(x) 的经验风险函数最小了,因为它对历史的数据拟合的最好。但是我们从图上来看f3(x) 肯定不是最好的,因为它过度学习历史数据,导致它在真正预测时效果会很不好,这种情况称为过拟合(over-fitting)。
为什么会造成这种结果?大白话说就是它的函数太复杂了,都有四次方了,这就引出了下面的概念,我们不仅要让经验风险最小化,还要让结构风险最小化。这个时候就定义了一个函数 J(f) ,这个函数专门用来度量模型的复杂度,在机器学习中也叫正则化(regularization)。常用的有 L1 ,L2 范数。
到这一步我们就可以说我们最终的优化函数是
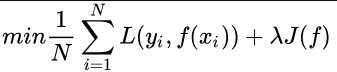
即最优化经验风险和结构风险,而这个函数就被称为目标函数。
此时结构化风险的定义为
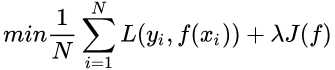
结合上面的例子来分析:最左面的 f1(x)结构风险最小(模型结构最简单),但是经验风险最大(对历史数据拟合的最差);最右面的f3(x) 经验风险最小(对历史数据拟合的最好),但是结构风险最大(模型结构最复杂);而 f2(x) 达到了二者的良好平衡,最适合用来预测未知数据集。
标签:ast 常用 利用 nbsp 概率 function error 训练 实际应用
原文地址:https://www.cnblogs.com/ziytong/p/12820684.html