标签:更新 col 拼接 优先 技术 dep img int 解法
题目:
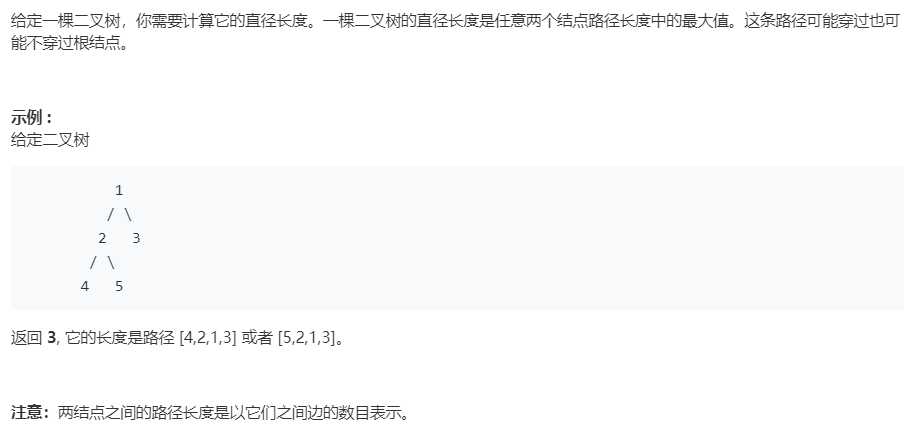
解法:
方法:深度优先搜索
首先我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。
而任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到。
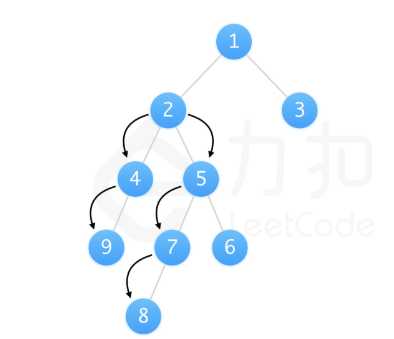
如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2为起点,从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。
假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 L (即以左儿子为根的子树的深度) 和其右儿子向下遍历经过最多的节点数 R(即以右儿子为根的子树的深度),那么以该节点为起点的路径经过节点数的最大值即为 L+R+1 。
我们记节点node 为起点的路径经过节点数的最大值为 d_node,那么二叉树的直径就是所有节点 d_node的最大值减一。
最后的算法流程为:我们定义一个递归函数 depth(node) 计算 d_node,函数返回该节点为根的子树的深度。先递归调用左儿子和右儿子求得它们为根的子树的深度 L和 R ,则该节点为根的子树的深度即为max(L,R)+1。
该节点的 d_node值为L+R+1。
递归搜索每个节点并设一个全局变量 ans 记录 d_node的最大值,最后返回 ans-1 即为树的直径。
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 int ans; 12 int depth(TreeNode* rt) 13 { 14 if (rt == NULL) 15 { 16 return 0; // 访问到空节点了,返回0 17 } 18 19 int L = depth(rt->left); // 左儿子为根的子树的深度 20 int R = depth(rt->right); // 右儿子为根的子树的深度 21 22 ans = max(ans, L + R + 1); // 计算d_node即L+R+1 并更新ans 23 24 return max(L, R) + 1; // 返回该节点为根的子树的深度 25 } 26 public: 27 int diameterOfBinaryTree(TreeNode* root) 28 { 29 ans = 1; 30 depth(root); 31 return ans - 1; 32 } 33 };
标签:更新 col 拼接 优先 技术 dep img int 解法
原文地址:https://www.cnblogs.com/ocpc/p/12821682.html