标签:public nod const style 思路 图片 col 面试题 tree
题目:
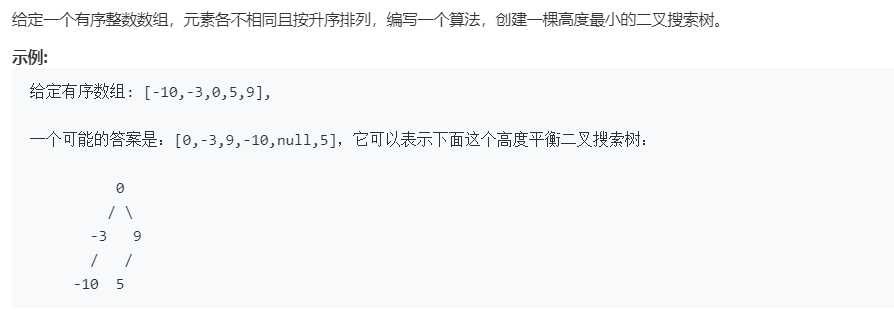
解答:
首先复习下二叉搜索树的定义:对于树中的所有子树都有,左子树上的值都小于根节点的值,右子树上的值都大于根节点上的值。
总结一下就是,树的中序遍历可以得到一个升序序列。
那如何保证高度最小呢?当树中的任意结点的左右子树高度差都不超过 1 时,整棵树的深度最小。
下面是一种构造最小高度树的思路:
(1)如果序列长度为 0,那么是一棵空树。
(2)如果序列长度为 1,那么只有一个根节点。
(3)如果长度大于 1,那么选取中间位置的数赋给根节点,然后前一半递归构建左子树,后一半递归构建右子树。
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* dfs(const vector<int> &nums, int L, int R) 13 { 14 if(L > R) 15 { 16 return nullptr; 17 } 18 int mid = (L+R)>>1; 19 auto ptr = new TreeNode(nums[mid]); //填充根节点 20 ptr->left = dfs(nums, L, mid-1); //构造左子树 21 ptr->right = dfs(nums, mid+1, R); //构造右子树 22 return ptr; 23 } 24 TreeNode* sortedArrayToBST(vector<int>& nums) 25 { 26 return dfs(nums, 0, nums.size()-1); 27 } 28 };
标签:public nod const style 思路 图片 col 面试题 tree
原文地址:https://www.cnblogs.com/ocpc/p/12822251.html