标签:回归 平面 测试数据 sig too code 介绍 数学推导 圆点
一、SVM算法原理及数学推导
1、支撑向量机,SVM(Support Vector Machine),其实就是一个线性分类器。在最初接到这个算法时,我们可能会一头雾水:这个名词好奇怪[问号脸],怎么“支持”?什么“向量”,哪来的“机”?
本篇文章从“不适定问题”开始介绍SVM的思想,通过支撑向量与最大间隔引申到如何将其转换为最优化问题,并数学推导求解有条件限制的最优化问题。相信学完本篇之后,大家一定会对SVM算法有一个大体上的认识。
首先,我们看一个简单的二分类问题。在二维的特征平面中,所有的数据点分为了两类:蓝色圆形和黄色三角。我们的目标是找到了一条决策边界,将数据分类。但实际上我们可以找到多条决策边界。
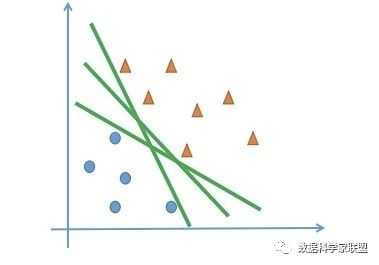
这就所谓的“不适定问题”。“不适定问题”会影响模型的泛化性。比如在下面的模型中,被黄色箭头标出的点被决策边界划为蓝色圆点,但实际上它和黄色三角更近一些。也就说决策边界的选择,不仅要考虑已经存在的数据上的是否分类正确,还要考虑是否能够更好地划分未出现的测试数据:
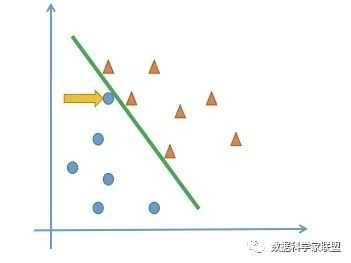
逻辑回归算法如何解决“不适定问题”问题呢?首先定义一个概率函数sigmoid函数:
二、SVM算法中的核函数
三、 SVM算法解决分类问题及回归问题
标签:回归 平面 测试数据 sig too code 介绍 数学推导 圆点
原文地址:https://www.cnblogs.com/zym-yc/p/12822692.html