SVM个人推导

时间：2020-05-04 13:25:22 阅读：49 评论：0 收藏：0 [点我收藏+]

SVM问题

SVM解决二分类问题，初始有一些点$X = [x_1, x_2, ..., x_n]$, 每一个点对应一个类别$y = 1 \quad or \quad y = -1$, SVM在高维空间中找一个超平面将样本点尽可能分开，而且分的时候是找一个间隔最大化的分离超平面。

最简单的情形的公式

原问题

$max_{w,b} \quad \gamma$
$s.t. \quad y_i(\frac{w}{||w||}\cdot x_i + \frac{b}{||w||}) \geq \gamma \quad i = 1, 2, ... N$
$\Rightarrow$
$max_{w,b} \quad \frac{\gamma}{||w||}$
$s.t. \quad y_i(w\cdot x_i + b) \geq \gamma \quad i = 1, 2, ... N$
另$\gamma = 1$
$max_{w,b} \quad \frac{1}{||w||}$
$s.t. \quad y_i(w\cdot x_i + b) \geq 1 \quad i = 1, 2, ... N$
$\Leftrightarrow$
$min_{w,b} \quad \frac{1}{2}*||w||^2 \tag{1}$
$s.t. \quad 1 - y_i(w\cdot x_i + b) \leq 0 \quad i = 1, 2, ... N \tag{2}$
这个就是需要求解的问题了，求解这个问题需要利用拉格朗日乘子法构造拉格朗日函数，在求解其对偶问题得到原始问题的最优解$w^*, b^*$

对偶问题

拉格朗日函数$L(w, b, a) = \frac{1}{2}*||w||^2 - \sum_{i=1}^{N}a_i*(y_i(w\cdot x_i + b)-1) ,a_i\geq0, i = 1, 2, ... N$
之所以求解对偶函数有两个原因

对偶问题更容易求解
能更加自然的引入核函数

由于$(2)$式的约束，$max_a L(w, b, a) = \frac{1}{2}*||w||^2$，所以原问题等价于

\[min_{w,b}max_{a} \quad L(w, b, a)\s.t. \quad 1 - y_i(w\cdot x_i + b) \leq 0 \quad i = 1, 2, ... N\]

满足KKT条件（这一点需要一些其他知识，此处从略），可以交换min，max，可得对偶问题

\[max_{a}min_{w,b} \quad L(w, b, a) \\ s.t. a_i \geq 0 \tag{3} \]

求解$min_{w,b} \quad L(w, b, a)$，求L对w和b的偏导

\[\bigtriangledown_wL = w - \sum_{i=1}^{N}a_iy_ix_i = 0 \\\bigtriangledown_bL = -\sum_{i=1}^{N}a_iy_i = 0 \]

$\Rightarrow w^* = \sum_{i=1}^{N}a_iy_ix_i$

则

\[min_{w,b} \quad L(w, b, a) = L(w^*, b, a) = \frac{1}{2}\sum_{i=1}^{N}a_iy_ix_i^T\sum_{j=1}^{N}a_jy_jx_j - \sum_{i=1}^{N}a_iy_ix_i^T\sum_{j=1}^{N}a_jy_jx_j - b\sum_{i=1}^{N}a_iy_i + \sum_{i=1}^{N}a_i \\ = \sum_{i=1}^{N}a_i - \frac{1}{2}\sum_{i=1}^{N}a_iy_ix_i^T\sum_{j=1}^{N}a_jy_jx_j \]

所以对偶问题变为：

\[max_a \sum_{i=1}^{N}a_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_ia_jy_iy_j(x_i^Tx_j)\\s.t. \quad \sum_{i=1}^{N}a_iy_i = 0, a_i\geq0\\ \Rightarrow \]

\[\\ min_a -\sum_{i=1}^{N}a_i + \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_ia_jy_iy_j(x_i^Tx_j)\\s.t. \quad \sum_{i=1}^{N}a_iy_i = 0, a_i\geq0 \tag{4} \]

这是一个二次规划问题，假设可以有很好的方法求解（SMO算法），解得$a^*$

最终判别函数

根据对偶问题的解$a^*$ 得出

$w^* = \sum_{i=1}^{N}a_i^*y_ix_i$

由(2)式的约束，在求$max_a L(w, b, a)$时可以看出 $a_i^*$有一个性质，在非支持向量的点$x_i$处，$a_i^* = 0$，只有在支持向量处，$a_i^* > 0$

我们假设已经求出$a^*$, 我们选择一个大于0的$a_k^*$, 则由于KKT中的互补条件$a_k^*(y_k(w\cdot x_k+b) - 1) = 0$得出

$y_k(w^*\cdot x_k + b) = 1$

$\Rightarrow$

$b^*= y_k - w^*\cdot x_k$

知道了$w^*, b^*$，我们可以得到最终想要的判别函数即分离超平面$f(x)=w^*\cdot x+b^*=\sum_{i=1}^{N}a_i^*y_i(x_i\cdot x) + y_k - \sum_{i=1}^{N}a_i^*y_i(x_i\cdot x_k), a_k^*>0$

但是还有一个问题没有解决，如何求解(4)那个二次规划问题，这时有一个SMO算法，最后进行解释

软间隔

以上适用于线性可分情形的推导，但实际情况下会遇到线性不可分，我们需要软间隔，允许少量样本不满足约束

$y_i(w\cdot x_i + b) \geq 1$

所以对每一个样本点加入一个松弛变量$\xi_i$，并对这个松弛变量增加惩罚参数$C$，原问题变为

\[min_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum_{i=1}^{N}\xi_i \\ s.t. \quad y_i(w\cdot x_i + b \geq 1 - \xi_i)\geq1-\xi_i, \\ \xi_i \geq 0, i = 1, 2, ... N \tag{5} \]

同之前的步骤，转换为对偶问题求解，先写出拉格朗日函数

$L(w, b, \xi, a, b) = \frac{1}{2}||w||^2+C\sum_{i=1}^{N}\xi_i - \sum_{i=1}^{N}a_i(y_i(w\cdot x_i + b)-1 + \xi_i) - \sum_{i=1}^{N}b_i\xi_i$

对偶问题为

\[max_{a, b}min_{w,b,\xi}\quad L \\ s.t. \quad a_i \geq 0, b_i \geq 0 \]

求$L$对$w,b,\xi$的偏导

\[\bigtriangledown_wL = w - \sum_{i=1}^{N}a_iy_ix_i = 0 \\\bigtriangledown_bL = -\sum_{i=1}^{N}a_iy_i = 0 \\ \bigtriangledown_{\xi}L=C\cdot[1,1,...,1]^T-a-b = 0 \]

$\Rightarrow$

\[w^* = \sum_{i=1}^{N}a_iy_ix_i \\ \sum_{i=1}^{N}a_iy_i = 0 \\ C = a_i +b_i \]

带入L得出$min_{w,b,\xi}L = \frac{1}{2}\sum_{i=1}^{N}a_iy_ix_i^T\sum_{j=1}^{N}a_jy_jx_j - \sum_{i=1}^{N}a_iy_ix_i^T\sum_{j=1}^{N}a_jy_jx_j - b\sum_{i=1}^{N}a_iy_i + \sum_{i=1}^{N}a_i + \sum_{i=1}^{N}(C-a_i-b_i)\xi_i \\ = \sum_{i=1}^{N}a_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_ia_jy_iy_j(x_i^Tx_j)$

对偶问题变为一个二次优化问题（注意，$b_i$被消去了）

\[min_{a}-\sum_{i=1}^{N}a_i + \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_ia_jy_iy_j(x_i^Tx_j) \\ s.t.\sum_{i=1}^{N}a_iy_i = 0, 0\leq a_i\leq C, i=1,2,...,N \]

同样使用SMO算法解这个二次优化问题，得出$a^*$，进而求出

$w* = \sum_{i=1}^{N}a_i^*y_ix_i$

根据KKT的互补条件：$a_i(y_i(w\cdot x_i + b)-1 + \xi_i) = 0$，$b_i\xi_i = 0$

选择一个$0 < a_k^* < C$，则因为$C=a_i+b_i$，所以$b_k^* > 0$，所以$\xi_k = 0$，所以

\[y_k(w^*\cdot x_k + b)-1 = 0 \\ \Rightarrow b^* = y_k - w^* \cdot x_k \]

最终得到的分离超平面为：

$f(x)=w^*\cdot x+b^*=\sum_{i=1}^{N}a_i^*y_i(x_i\cdot x) + y_k - \sum_{i=1}^{N}a_i^*y_i(x_i\cdot x_k), C>a_k^*>0$

和原始的结果一样，只不过选择$a_k^*$时的范围限制有了变化

非线性

但其实即使有软间隔，对与实际情况也有许多偏差，很多实际情况是非线性的，这是就需要用到一个核技巧：使用一个变换将原空间的数据映射到新空间(例如更高维甚至无穷维的空间)；然后在新空间里用线性方法从训练数据中学习得到模型。

这个变换通过一个核函数K完成，一个关键是核函数是什么，通常使用常用的正定核函数就可以了

多项式核函数 $K(x,z)=(x\cdot z + 1) ^ p$
高斯核函数 $K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2})$ （比较常用）

关于核函数背后有很多数学知识，可以参见

RBF 核函数背后隐藏着怎样的映射

关于核函数的调参，scikit-learn使用网格搜索的方法来调，参见

支持向量机高斯核调参小结

使用这个核函数也简单，将原先的内积变成核函数即可，对偶问题最后要求解的二次优化问题就变成了：

\[min_{a}-\sum_{i=1}^{N}a_i + \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}a_ia_jy_iy_jK(x_i,x_j) \\ s.t.\sum_{i=1}^{N}a_iy_i = 0, 0\leq a_i\leq C, i=1,2,...,N \tag{6} \]

利用SMO算法解出$a^*$之后求出

$w* = \sum_{i=1}^{N}a_i^*y_ix_i$

$b^* = y_k - \sum_{i=1}^{N}a_i^*y_iK(x_i,x_k), 0 < a_k^* < C$

最后得出分离超平面为

$f(x)=w^*\cdot x+b^*=\sum_{i=1}^{N}a_i^*y_iK(x_i, x) + y_k - \sum_{i=1}^{N}a_i^*y_iK(x_i, x_k), C>a_k^*>0$

SMO算法

说了这么多一个关键的问题是（6）这个二次优化问题如何解决，针对SVM的一个比较快的算法是SMO算法。

SMO算法是迭代跟新参数得到最终值的，一开始会设定一个$a=[a_1,a_2,...,a_n]$，然后选择两个变量，固定其他变量为常量，迭代更新这两个变量直到收敛，然后在更新其他变量。

至于选择哪两个变量有启发式的算法，第一个变量选择$0 < a_k < C$的变量，第二个变量$a_j$最大化$|E_k - E_j|$，这里我们忽略这个启发式选择的算法，假设我们选择$a_1,a_2$进行更新，看一下SMO每一次是如何迭代更新参数的。

求原始解

简化式子，我们设$K_{ij}=K(x_i,x_j)$，固定除$a_1,a_2$的其他参数，得到要优化的式子：

\[W(a_1,a_2)=-a_1-a_2+\frac{1}{2}K_{11}a_1^2 + \frac{1}{2}K_{22}a_2^2+K_{12}y_1y_2a_1a_2+y_1a_1\sum_{i=3}^{N}a_iy_ik_{i1}+y_2a_2\sum_{i=3}^{N}a_iy_ik_{i2} \\ +\frac{1}{2}\sum_{i=3}^{N}\sum_{j=3}^{N}a_ia_jy_iy_jK_{ij}-\sum_{i=3}^{N}a_i \tag{7} \]

设

$\frac{1}{2}\sum_{i=3}^{N}\sum_{j=3}^{N}a_ia_jy_iy_jK_{ij}-\sum_{i=3}^{N}a_i = Z$

$\sum_{i=3}^{N}a_iy_ik_{i1} = v_1$

$\sum_{i=3}^{N}a_iy_ik_{i2}=v_2$

根据（6）的约束$\sum_{i=1}^{N}a_iy_i = 0$得出：

$a_1y_1+a_2y_2=-\sum_{i=3}^{N}a_iy_i = \varsigma $

$\Rightarrow$

$a_1=\varsigma y_1-a_2y_1y_2$

将上面的式子带入（7）有

\[W(a_2)=-(\varsigma y_1-a_2y_1y_2)-a_2+\frac{1}{2}K_{11}(\varsigma y_1-a_2y_1y_2)^2+\frac{1}{2}K_{22}a_2^2+K_{12}y_1y_2a_2(\varsigma y_1-a_2y_1y_2)+y_2v_2a_2+y_1v_1(\varsigma y_1-a_2y_1y_2)+Z \]

$\frac{\partial W}{\partial a_2} = (K_{11}+K_{22}-2K_{12})a_2+y_1y_2-1+(K_{12}-K_{11})y_2\varsigma+y_2(v_2-v_1)=0 \tag{8}$

但是根据这个偏导得出的$a_2$没有迭代关系，需要一些变化

求出$a$后最后的判别函数为$f(x)=\sum_{i=1}^{N}a_iy_iK(x_i,x)+b$，这个式子中的b也是要更新的，这个后面再说。根据这个判别函数，我们可以用其表示$v_1,v_2$

$v_1=f(x_1)-a_1y_1k_{11}-a_2y_2k_{12}-b$

$v_2=f(x_2)-a_1y_1k_{12}-a_2y_2k_{22}-b$

$\Rightarrow$

$v_2-v_1 = f(x_2) - f(x_1) - \varsigma (K_{12}-K_{11}) +a_2y_2(2K_{12}-K_{11}-K_{22})$

这里的$a_2$是旧的，记为$a_2^{old}$;（8）式的$a_2$是新的，记为$a_2^{new}$。将其带入（8）得：

\[\frac{\partial W}{\partial a_2} = (K_{11}+K_{22}-2K_{12})a_2^{new}+y_1y_2-1+(K_{12}-K_{11})y_2\varsigma+y_2(f(x_2) - f(x_1) - \varsigma (K_{12}-K_{11}) +a_2^{old}y_2(2K_{12}-K_{11}-K_{22})) \\ = y_2(y_1-y_2+f(x_2)-f(x_1)) + (K_{11}+K_{22}-2K_{12})(a_2^{new}-a_2^{old}) = 0 \]

这里还把$\varsigma$消掉了。

记$E_i = f(x_i) - y_i, \quad \eta=K_{11}+K_{22}-2K_{12}$

得$a_2^{new} = \frac{y_2(E_1 - E_2)}{\eta} + a_2^{old}$

修剪原始解

SVM中我们的$a_i$是有约束的，所有得到的$a_2^{new}$需要满足约束，将为被约束修剪的$a_2^{new}$记为$a_2^{new,unclipped}$

我们的约束是一个正方形约束：

\[a_1y_1+a_2y_2=-\sum_{i=3}^{N}a_iy_i = \varsigma \\ 0 \leq a_2 \leq C \\ 0 \leq a_1 \leq C \]

技术图片

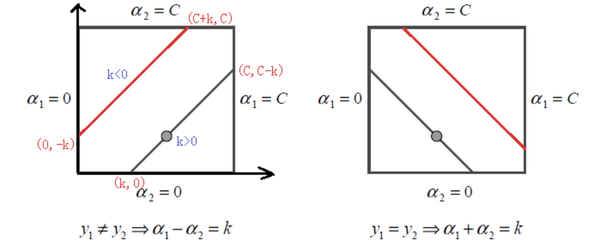
当$y_1!=y_2$时，$a_2-a_1=k(这个k没有什么意义，后面求上下界时用a_2^{old}-a_1^{old}表示)$

下界$L=max(0, a_2^{old}-a_1^{old})$

上界$H= min (C, C+a_2^{old}-a_1^{old})$

当$y_1=y_2$时，$a_2+a_1=k$

下界$L=max(0, a_2^{old}+ a_1^{old}-C)$

上界$H= min (C, a_2^{old}+a_1^{old})$

根据$L$和$H$，修剪过后的值为

\[a_2^{new} = \left\{\begin{matrix} H& a_2^{new,unclipped}>H\\ a_2^{new,unclipped}& L\leq a_2^{new,unclipped} \leq H\\ L& a_2^{new,unclipped} < L \end{matrix}\right.\]

得到$a_2^{new}$后，根据$a_1^{new}y_1+a_2^{new}y_2 = a_1^{old}y_1+a_2^{old}y_2$得

$a_1^{new}=a_1^{old}+y_1y_2(a_2^{old}-a_2^{new})$

这样我们就可以根据$a_1^{old},a_2^{old}$更新$a_1^{new},a_2^{new}$了