标签：耦合性   form   机器学习   参数   ova   net   文章   AMM   normal   

特征缩放

to do

Batch Normalization原理

https://zhuanlan.zhihu.com/p/34879333
https://zhuanlan.zhihu.com/p/69659844
https://zhuanlan.zhihu.com/p/54530247

背景

• 对深层神经网络的训练调参困难且复杂，深度神经网络之所以如此难训练，其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性
• 网络中层与层之间的关联性会导致如下的状况：随着训练的进行，网络中的参数也随着梯度下降在不停更新
  • 当底层网络中参数发生微弱变化时，由于每一层中的线性变换与非线性激活映射，这些微弱变化随着网络层数的加深而被放大（类似蝴蝶效应）；
  • 参数的变化导致每一层的输入分布会发生改变，进而上层的网络需要不停地去适应这些分布变化，使得我们的模型训练变得困难。
    上述这一现象叫做*Internal Covariate Shift(内部协变量偏移)**

什么叫Internal Covariate Shift

• 官方：深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift
  

Internal Covariate Shift会带来什么问题？

• 上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低
  • 梯度下降的过程会让每一层的参数发生变化，进而使得每一层的线性与非线性计算结果分布产生变化，后层网络就要不停地去适应这种分布变化，这个时候就会使得整个网络的学习速率过慢。
• 网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度
  • 当我们在神经网络中采用饱和激活函数时，例如sigmoid，tanh激活函数，很容易使得模型训练陷入梯度饱和区（saturated regime）。随着模型训练的进行，我们的参数会逐渐更新并变大，此时激活值就会随之变大，并且激活值还受到更底下的多个曾层网络参数的影响，随着网络层数的加深，激活值很容易陷入梯度饱和区(比如sigmoid值接近1)，此时梯度会变得很小甚至接近于0，参数的更新速度就会减慢，进而就会放慢网络的收敛速度。
  • 对于激活函数梯度饱和问题，有两种解决思路。第一种就是更为非饱和性激活函数，例如线性整流函数ReLU可以在一定程度上解决训练进入梯度饱和区的问题。另一种思路是，我们可以让激活函数的输入分布保持在一个稳定状态来尽可能避免它们陷入梯度饱和区，这也就是Normalization的思路。比如使得每层的输入都在均值为0，方差为1的区域附近，这时由sigmoid的函数可以知道，肯定是有梯度的。

如何减缓Internal Covariate Shift(ICS)?

• ICS产生的原因是由于参数更新带来的网络中每一层输入值分布的改变，并且随着网络层数的加深而变得更加严重，因此我们可以通过固定每一层网络输入值的分布来对减缓ICS问题。
  • 白化（Whitening）: 是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换，进而达到以下两个目的：使得输入特征分布具有相同的均值与方差。其中PCA白化保证了所有特征分布均值为0，方差为1；而ZCA白化则保证了所有特征分布均值为0，方差相同；去除特征之间的相关性。通过白化操作，我们可以减缓ICS的问题，进而固定了每一层网络输入分布，加速网络训练过程的收敛（LeCun et al.,1998b；Wiesler&Ney,2011）
  • 问题在于：白化过程计算成本太高，并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作；白化过程由于改变了网络每一层的分布，因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
    新思路：一方面，我们提出的normalization方法要能够简化计算过程；另一方面又需要经过规范化处理后让数据尽可能保留原始的表达能力。

Batch Normalization

• 既然白化计算过程比较复杂，那我们就简化一点，比如我们可以尝试单独对每个特征进行normalizaiton就可以了，让每个特征都有均值为0，方差为1的分布就OK。
• 另一个问题，既然白化操作减弱了网络中每一层输入数据表达能力，那我就再加个线性变换操作，让这些数据再能够尽可能恢复本身的表达能力就好了。
  

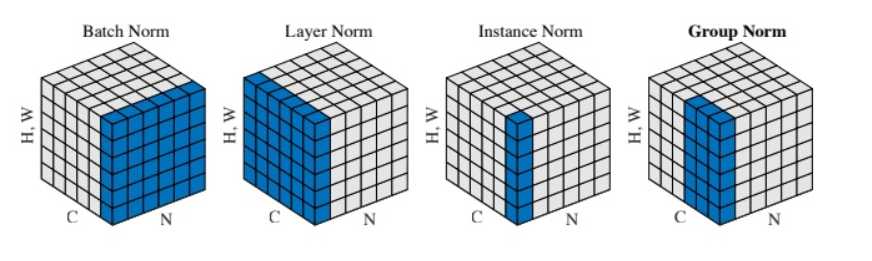
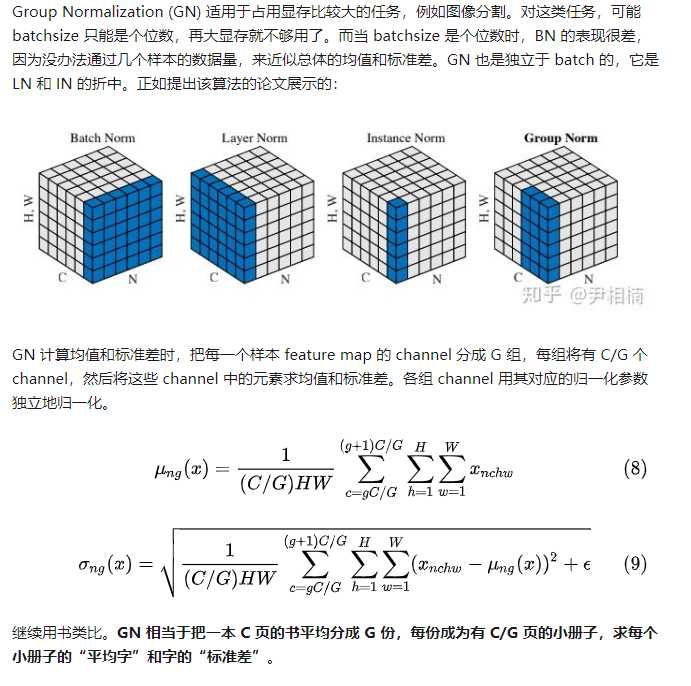
比如给定[N,C,HW]，在[N,HW]上计算均值向量[C], 方差向量[C]
我们解决了第一个问题，即用更加简化的方式来对数据进行规范化，使得第 [公式] 层的输入每个特征的分布均值为0，方差为1。
Normalization操作我们虽然缓解了ICS问题，让每一层网络的输入数据分布都变得稳定，但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达（representation ability of the network），使得底层网络学习到的参数信息丢失。

测试阶段如何使用Batch Normalization？

最好不要在测试阶段用,因为

非要用的话

Batch Normalization的优势

BN使得网络中每层输入数据的分布相对稳定，加速模型学习速度

BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内，使得后一层网络不必不断去适应底层网络中输入的变化，从而实现了网络中层与层之间的解耦，允许每一层进行独立学习，有利于提高整个神经网络的学习速度。

BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定

当学习率设置太高时，会使得参数更新步伐过大，容易出现震荡和不收敛。但是使用BN的网络将不会受到参数数值大小的影响

BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题

在神经网络中，我们经常会谨慎地采用一些权重初始化方法（例如Xavier）或者合适的学习率来保证网络稳定训练。
在不使用BN层的时候，由于网络的深度与复杂性，很容易使得底层网络变化累积到上层网络中，导致模型的训练很容易进入到激活函数的梯度饱和区；通过normalize操作可以让激活函数的输入数据落在梯度非饱和区，缓解梯度消失的问题；另外通过自适应学习 \(\gamma\) 与 \(\beta\) 又让数据保留更多的原始信息。

BN具有一定的正则化效果

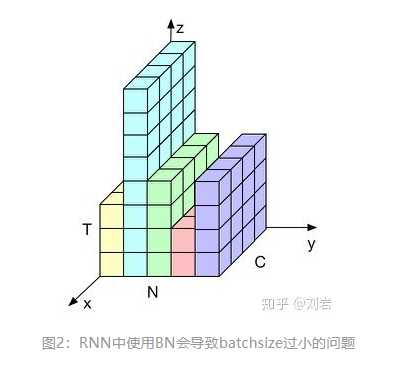
在Batch Normalization中，由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计，尽管每一个batch中的数据都是从总体样本中抽样得到，但不同mini-batch的均值与方差会有所不同，这就为网络的学习过程中增加了随机噪音，与Dropout通过关闭神经元给网络训练带来噪音类似，在一定程度上对模型起到了正则化的效果。

BN总结

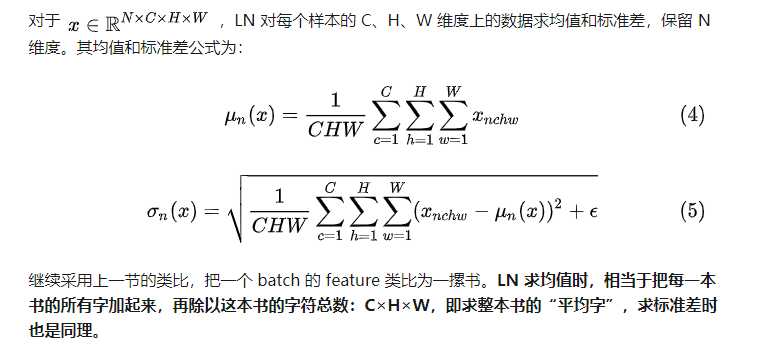
神经网络中有各种归一化算法：Batch Normalization (BN)、Layer Normalization (LN)、Instance Normalization (IN)、Group Normalization (GN)。从公式看它们都差不多，如 (1) 所示：无非是减去均值，除以标准差，再施以线性映射。

BN实现

# coding=utf8
import torch
from torch import nn

# track_running_stats=False，求当前 batch 真实平均值和标准差，而不是更新全局平均值和标准差
# affine=False, 只做归一化，不乘以 gamma 加 beta（通过训练才能确定）
# num_features 为 feature map 的 channel 数目
# eps 设为 0，让官方代码和我们自己的代码结果尽量接近
bn = nn.BatchNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)

# 乘 10000 为了扩大数值，如果出现不一致，差别更明显
x = torch.rand(10, 3, 5, 5)*10000 
official_bn = bn(x)

# 把 channel 维度单独提出来，而把其它需要求均值和标准差的维度融合到一起
x1 = x.permute(1,0,2,3).view(3, -1) # [N,C,H,W]==>[C,N,H,W]==>[C=3, N*H*W]
 
mu = x1.mean(dim=1).view(1,3,1,1) # [C, N*H*W]==>[C]==>[1, C, H, W]
std = x1.std(dim=1, unbiased=False).view(1,3,1,1)
# unbiased=False, 求方差时不做无偏估计（除以 N-1 而不是 N），和原始论文一致,个人感觉无偏估计仅仅是数学上好看，实际应用中差别不大


my_bn = (x-mu)/std

diff=(official_bn-my_bn).sum()
print(‘diff={}‘.format(diff)) # 差别是 10-5 级的，证明和官方版本基本一致

Layer Normalization 实现

• BN 的一个缺点是需要较大的batchsize 才能合理估训练数据的均值和方差，这导致内存很可能不够用
  
• 同时它也很难应用在训练数据长度不同的 RNN 模型上 （序列数据: [N, C, T=MAX_LEN]）
  • 在一个batch中，通常各个样本的长度都是不同的，当统计到比较靠后的时间片时，假设这时只有一个样本还有数据(其他全是padding了)，基于这个样本的统计信息不能反映全局分布，所以这时BN的效果并不好。
  • 如果测试时要用BN的话，如果在测试时我们遇到了长度大于任何一个训练样本的测试样本，我们无法找到保存的归一化统计量，所以BN无法运行。
• LN能减轻ICS,至少LN将每个训练样本都归一化到了相同的分布上。而在BN的文章中介绍过几乎所有的归一化方法都能起到平滑损失平面的作用。所以从原理上讲，LN能加速收敛速度的。
• LN是在[C, H*W]这个平面计算均值和方差，最后输出维度是[N], 实质是单个样本内部的归一化
  

import torch
from torch import nn

x = torch.rand(10, 3, 5, 5)*10000

# normalization_shape 相当于告诉程序这本书有多少页，每页多少行多少列
# eps=0 排除干扰
# elementwise_affine=False 不作映射
# 这里的映射和 BN 以及下文的 IN 有区别，它是 elementwise 的 affine，
# 即 gamma 和 beta 不是 channel 维的向量，而是维度等于 normalized_shape 的矩阵
ln = nn.LayerNorm(normalized_shape=[3, 5, 5], eps=0, elementwise_affine=False)

official_ln = ln(x)

x1 = x.view(10, -1)
mu = x1.mean(dim=1).view(10, 1, 1, 1)
std = x1.std(dim=1,unbiased=False).view(10, 1, 1, 1)

my_ln = (x-mu)/std

diff = (my_ln-official_ln).sum()

print(‘diff={}‘.format(diff)) # 差别和官方版本数量级在 1e-5

Instance Normalization

import torch
from torch import nn


x = torch.rand(10, 3, 5, 5) * 10000

# track_running_stats=False，求当前 batch 真实平均值和标准差，
# 而不是更新全局平均值和标准差
# affine=False, 只做归一化，不乘以 gamma 加 beta（通过训练才能确定）
# num_features 为 feature map 的 channel 数目
# eps 设为 0，让官方代码和我们自己的代码结果尽量接近
In = nn.InstanceNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)

official_in = In(x)

x1 = x.view(30, -1)
mu = x1.mean(dim=1).view(10, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 3, 1, 1)

my_in = (x-mu)/std

diff = (my_in-official_in).sum()
print(‘diff={}‘.format(diff)) # 误差量级在 1e-5

Group Normalization

import torch
from torch import nn


x = torch.rand(10, 20, 5, 5)*10000

# 分成 4 个 group
# 其余设定和之前相同
gn = nn.GroupNorm(num_groups=4, num_channels=20, eps=0, affine=False)
official_gn = gn(x)

# 把同一 group 的元素融合到一起
x1 = x.view(10, 4, -1)
mu = x1.mean(dim=-1).reshape(10, 4, -1)
std = x1.std(dim=-1).reshape(10, 4, -1)

x1_norm = (x1-mu)/std
my_gn = x1_norm.reshape(10, 20, 5, 5)

diff = (my_gn-official_gn).sum()

print(‘diff={}‘.format(diff)) # 误差在 1e-4 级

别人的总结

特征缩放和Batch Normalization

标签：耦合性   form   机器学习   参数   ova   net   文章   AMM   normal   

原文地址：https://www.cnblogs.com/doragd/p/12827090.html