标签：接下来 等价 src 改变 现在 增加 结果 屏幕 约束
影院角度问题
下图为影院的剖面示意图，座位的满意程度主要取决于视角α 和仰角 β 。视角α是观众眼睛到屏幕上、下边缘视线的夹角，α 越大越好；仰角 β 是观众眼睛到屏幕上边缘视线与水平线的夹角，β 太大使人的头部过分上仰，引起不舒服感，一般要求 β 不超过30度。 记影院屏幕高h ，上边缘距地面高 H，地板线倾角θ ，第一排和最后一排座位与屏幕水平距离分别为 d和 D ，观众平均座高为c（指眼睛到地面的距离）。已知参数 h=1.8,d = 4.5 ， D=19 ，c =1.1，H=5（单位：m）。
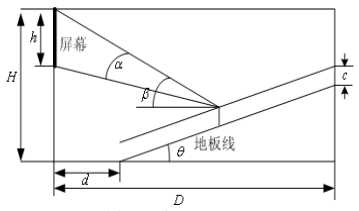
（1）地板线倾角θ =10 ，问最佳座位在什么地方?
（2）求地板线倾角（一般不超20 ），使所有观众的平均满意程度最大。
（3）地板线设计成什么形状可以进一步提高观众的满意程度。
摘要
对于问题1，首先根据满意度设置两种求解情况，第一种是当仰角β<=30时，由于角度较小，可以粗略的认为只要β<=30，就无须再考虑仰角对观众的影响。将视角α作为满意度依据，另一种当β>30时，同时考虑这两个角度对满意度的影响，同时设置α的影响因子p，和β的影响因子1-p，根据观众实际情况合理的设置p，这里拟合了不同的p对满意度的影响。通过MATLAB求出了距离屏幕6.2274m的距离观众满意度最佳。
对于问题2，将观众离散均匀分布，算出每一排距离屏幕的距离xi，然后利用问题一情况二的思路求出每一排的满意度Si，最后求和除以总的排数求出S。同时用不同的θ和p来拟合，找出不同p的情形下最大S对应的θ。
问题3从提高地板线和将地板线设计成折线这两个方面来提高满意度。
关键词：非线性规划 MATLAB 三角函数
一,问题提出
二,模型假设
假设题目给出的已知参数是合理的。
三,符号说明
S 平均满意度
Si 第i排的满意度
x 到屏幕的水平距离
xi 第i排到屏幕的水平距离
p 对α和β影响的权重
θ 重新设置的地板线角度
n 总的排数
四,模型建立与求解
4.1问题一的分析与求解
首先根据满意度设置两种求解情况，第一种是当仰角β<=30时，就将视角α作为满意度依据，另一种当β>30时，同时考虑这两个角度对满意度的影响，同时设置α的影响因子p，和β的影响因子1-p，根据观众实际情况合理的设置p，此处设置不同的p来拟合数据进而分析规律。
4.1.1问题一情况一的分析与求解
此时β<=30，只需考虑α的影响。首先确定各种关系表达式。设最佳位置到屏幕的水平距离为x,利用三角函数求得：
xtan(β-α)+h=xtan(β) .................(1)
tan(β-α)=(tan(β)-tan(α))/(1-tan(α)tan(β)).........(2)
xtan(β)+c+(x-d)tanθ =H................................(3)
由(1)(2)(3)联立求得：
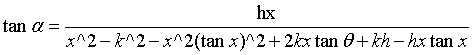............(4)
由于β<=30，则有tanβ<
，所以有x>(H-c+dtanθ)/(tanθ+)
且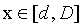
,注：k=H+dtanθ-c
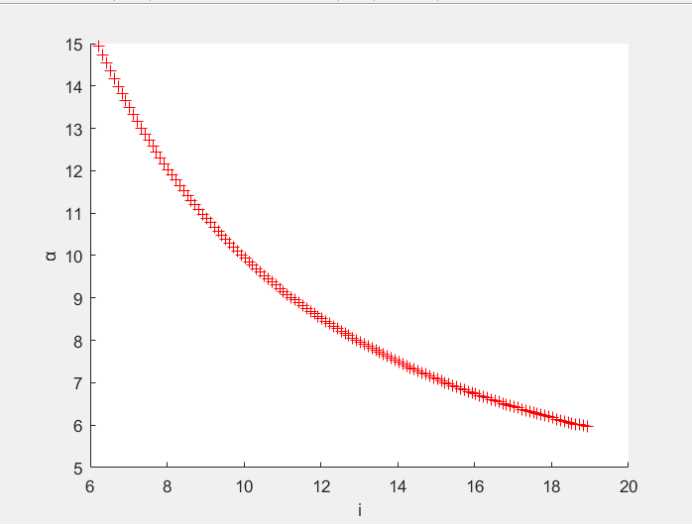
利用MATLAB模拟α关于x的图像如下，从中获取最大值。代码见附录1根据图像知在满足约束条件的情况下，可得α关于x单调递减，也就是说α最大可以取到大约14.9，此时即为情况1最大的满意度，对应的x=6.2274。
图1 α关于x的图像
4.1.2问题一情况二的分析与求解
根据题意知要使满意度最大，需要α尽可能大，β尽可能小，不同的地区的人可能对这两种影响因素的权值有不同的定义。现在取p=0.1一直到1，以0.1的步长对不同的p进行拟合。首先根据(4)(5)可以求出α，β则：
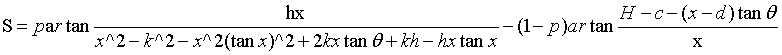
β>30
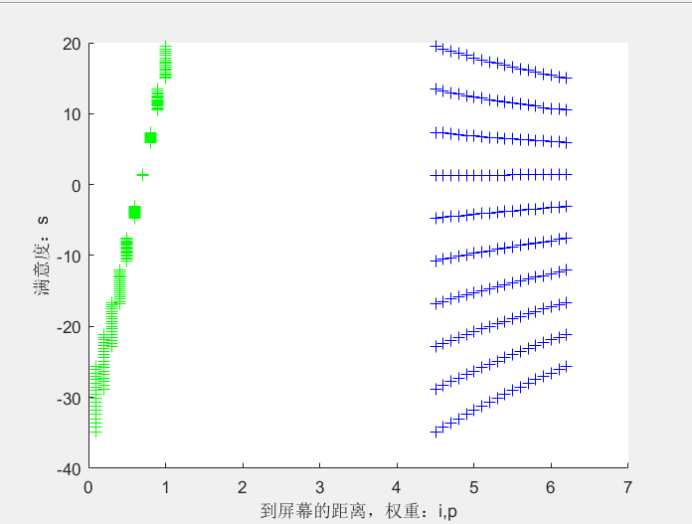
求得的图像如下，根据图分析，p的设置对于最大满意度影响较大，当p=1时，即回到了第一种情况，此时x<6.2274，而第一问中x>=6.2274，两处的衔接很吻合。如果取p=0.9，最大值约为13.2，若取p<=0.4，最大满意度为负值即说明当观众更在意仰头的体验度时，观众对该影院的体验度较差。当x<6.2274
即β>30其他所有的最大值都小于14.9，所以最大满意度为14.9。
图2 满意度s关于p,x的图像
4.2问题二的分析与求解
在第一问中用户满意度的计算分为两种情况，同理，统一考虑两种情况来求最大的平均满意度。对于地板线，将座位离散均匀的分布在上面，同一水平线上
的座位的满意度一样。每一排之间间隔一般为0.7m-1m这里取0.8m,0.8*18=14.4
所以一共可以有n=18排则有：
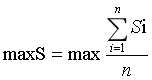...........................................(6)
β<=30，即xi>=(H-c+dtanθ)/(tanθ+
)时：
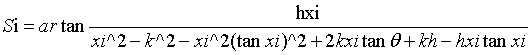......(7)
β>30，即xi<(H-c+dtanθ)/(tanθ+)时：
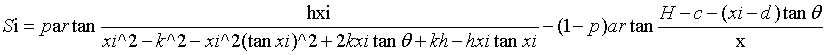.................(8)
利用MATLAB求解(求解代码见附录),角度约为13.4时有最大的平均满意度
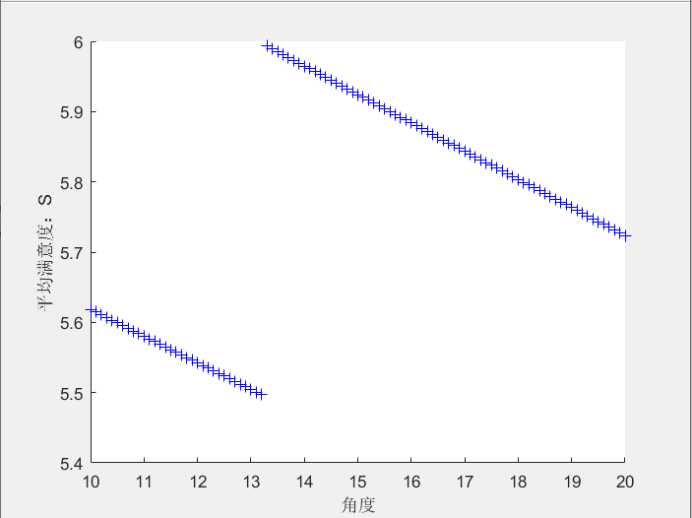
4.3问题三的分析与求解
对于每个固定的x，如果将观众的位置在y方向上提高，经过简单的画图分析提高座位高度可一定程度上提高某个位置的满意度。用模型一来探究高度对平均满意度的影响，此时为简便假设θ取第二问中求得的最佳角度。
在前面的讨论中地板线均是直线，那么考虑折线是否能提高满意度。首先可以先选取合适的一排z，在z之前不变，在z这一排又建立关系重新设定不同的角度。
4.3.1 模型一的求解与分析
尝试增加地板线的高度是否对增加满意度有效。设增加了t，依次从0.1以步长0.05增加到1。那么依然可以利用(6)(7)(8)式子，只是所有的H=H-t，但这并不意味这H减少t，而是升高的地板线的效果等价于这个，显然H很难改变。利用MATLAB拟合并求解。根据图分析可以当增高7厘米时效果有很大提升，然后缓提升，但到了65厘米时又有个大提升，但此时成本较高，综合考虑应取7厘米左右。这个模型对升高的较小高度有比较好的效果。
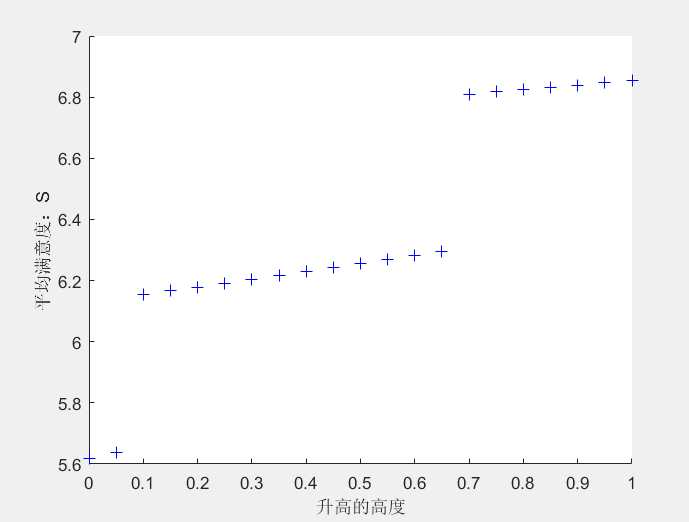
4.3.1 模型二的求解与分析
首先仍取第二问的最佳角度，利用MATLAB计算出每一排的满意度结果如下。可以发现后面的满意度偏低，所以将z设置在倒数第8排左右的位置，前十排的总满意度为64.571，第11排距离屏幕的距离为13.3m。接下来计算的后八排满意度和。依然可以利用(6)(7)(8)求解，解得越小越好，可以取第一问中的10，满意度和为47.9974，计算的S=6.2538，比之前的5.6893有所提高。
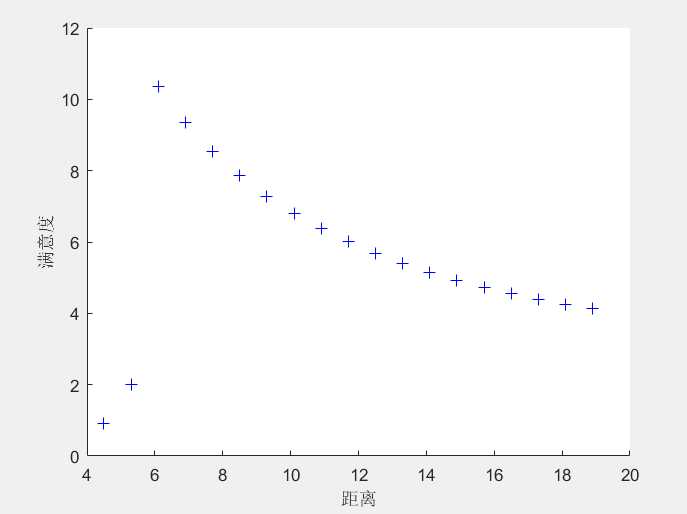
五,模型评价与推广
附录
!问题一情况1的求解
hold on
h=1.8;d=4.5;D=19;c=1.1;H=5;n=18;
x0=tan(2*10*pi/360);
k=h+d*tan(2*10*pi/360)-c;
x1=(H-c+d*x0)/(x0+tan(2*30*pi/360));
for i=x1:0.1:D
y0=h*i/(i^2-k^2-i^2*(tan(2*i*pi/360))^2+2*k*i*x0+k*h-k*h*(tan(2*i*pi/360))^2);
y=atand(y0);
plot(i,y,‘+r‘);
end
xlabel(‘i‘),ylabel(‘α‘)
!问题一情2的求解
hold on
h=1.8;d=4.5;D=19;c=1.1;H=5;n=18;
x0=tan(2*10*pi/360);k=h+d*tan(2*10*pi/360)-c;
x1=(H-c+d*x0)/(x0+tan(2*30*pi/360));xlabel(‘到屏幕的距离，权重：i,p‘),ylabel(‘满意度：s‘)
for p=0.1:0.1:1
for i=d:0.1:x1 s=p*atand(h*i/(i^2-k^2-i^2*(tan(2*i*pi/360))^2+2*k*i*x0+k*h-k*h*(tan(2*i*pi/360))^2))-(1-p)*atand((H-c+(d-i)*x0)/i);
plot(i,s,‘+b‘);plot(p,s,‘+g‘);
end
end
!问题二的求解
hold on
h=1.8;d=4.5;D=19;c=1.1;H=5;n=18;
k=h+d*tan(2*10*pi/360)-c;p=0.7;xlabel(‘½Ç¶È‘),ylabel(‘ƽ¾ùÂúÒâ¶È£ºS‘)
for t=10:0.1:20
S=0;
x0=tan(2*t*pi/360); x1=(H-c+d*x0)/(x0+tan(2*30*pi/360));
for xi=4.5:0.8:19
if xi<x1 S=S+p*atand(h*xi/(xi^2-k^2-xi^2*(tan(2*xi*pi/360))^2+2*k*xi*x0+k*h-k*h*(tan(2*xi*pi/360))^2))-(1-p)*atand((H-c+(d-xi)*x0)/xi);
else S=S+p*atand(h*xi/(xi^2-k^2-xi^2*(tan(2*xi*pi/360))^2+2*k*xi*x0+k*h-k*h*(tan(2*xi*pi/360))^2));
end
end
S=S/n;plot(t,S,‘+b‘);
End
!第三问模型一求解
hold on
h=1.8;d=4.5;D=19;c=1.1;H=5;n=18;m=0;
k=h+d*tan(2*10*pi/360)-c;p=0.7;xlabel(‘升高的高度‘),ylabel(‘平均满意度：S‘)
for d1=0:0.05:1
H=5;S=0;H=H-d1;
x0=tan(2*10*pi/360); x1=(H-c+d*x0)/(x0+tan(2*30*pi/360));
for xi=4.5:0.8:19
if xi<x1
S=S+p*atand(h*xi/(xi^2-k^2-xi^2*(tan(2*xi*pi/360))^2+2*k*xi*x0+k*h-k*h*(tan(2*xi*pi/360))^2))-(1-p)*atand((H-c+(d-xi)*x0)/xi);
else S=S+p*atand(h*xi/(xi^2-k^2-xi^2*(tan(2*xi*pi/360))^2+2*k*xi*x0+k*h-k*h*(tan(2*xi*pi/360))^2));
end
end
S=S/n;plot(d1,S,‘+b‘);end
标签：接下来 等价 src 改变 现在 增加 结果 屏幕 约束
原文地址：https://www.cnblogs.com/Lovely-Boy/p/12828814.html
