标签：兴趣 hang 参数 对比 目标 drop mda tle ons
知识追踪的主要任务是根据学生的历史学习轨迹来自动评价学生随着时间推移的知识点掌握程度变化。在了解学生的知识点掌握水平后，便可以为学生提供符合自身学情的个性化辅导。在教育行业中，利用科学方法有针对性地对学生的知识点掌握程度进行追踪还是十分有必要的。依据学生的海量历史学习数据可以完成对学生的学习过程建模，使模型能够自动追踪学生每个阶段的学习状态，从而达成自适应学习的目的。有学者认为，学生所掌握的知识点集合与其外在的做题表现间是有十分密切关联的，所以我们可以尝试通过学生的做题表现来建模学生的知识点掌握状态[1]。
一般来说，知识追踪任务可以表达成以下的数学形式：给定学生A在特定学习任务上的历史学习序列 Xt=(x1,x2,...xt)，来预测学生A的在xt+1上的表现。通常xt可以表示为一个有序对(qt,at)，该有序对中qt表示学生在t时刻回答的问题qt，而at则代表了学生在qt上的回答情况，一般而言at取值为0 （回答错误）或者1（回答正确）。其实，如果站在概率的角度上来看知识追踪，本质上是利用学生历史作答表现来预测学生在下一个时间点正确回答问题qt+1的概率，即P(at+1=1|qt+1,Xt)，可以被解释为在给定学生历史学习表现序列Xt 和在t+1时刻会做的题目qt+1的情况下，学生做对题目qt+1的概率大小。
在初步了解什么是知识追踪的概念后，我们接下来要介绍我们的主角——DKT（深度知识追踪）[2]。目前世界上有许多智能教育公司在使用知识追踪的相关模型，如BKT（贝叶斯知识追踪）和DKT（深度知识追踪），深度知识追踪简单直观来说就是利用深度学习方法来做知识追踪。从DKT论文中的实验结果发现，DKT在不需要过多专家经验和大量特征工程的情况下，精度优于传统方法。下面我们就来介绍下深度知识追踪算法DKT究竟是如何工作的。
为了让各个背景的伙伴都可以对DKT有一个好的了解，我们首先要简单说一下什么是DKT中使用的循环神经网络（RNN）[3]。传统的循环神经网络接受x1,...xT作为输入，然后输入映射到y1,...yT。这个可以通过隐变量h1,...hT达成，每个时刻下的隐变量都可以被看成过去所有信息的某种编码，用于和当下的输入一起与预测未来输出的结果。我们可以用以下公式来进行表达：
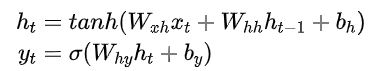
在上面的公式中， tanh()与σ()是激活函数，模型的主要参数包含输入权重Wxh、循环权重Whh、初始隐变量h0、输出权重Why以及隐变量与输出的截距bh与by。循环神经网络也可以简化成下图：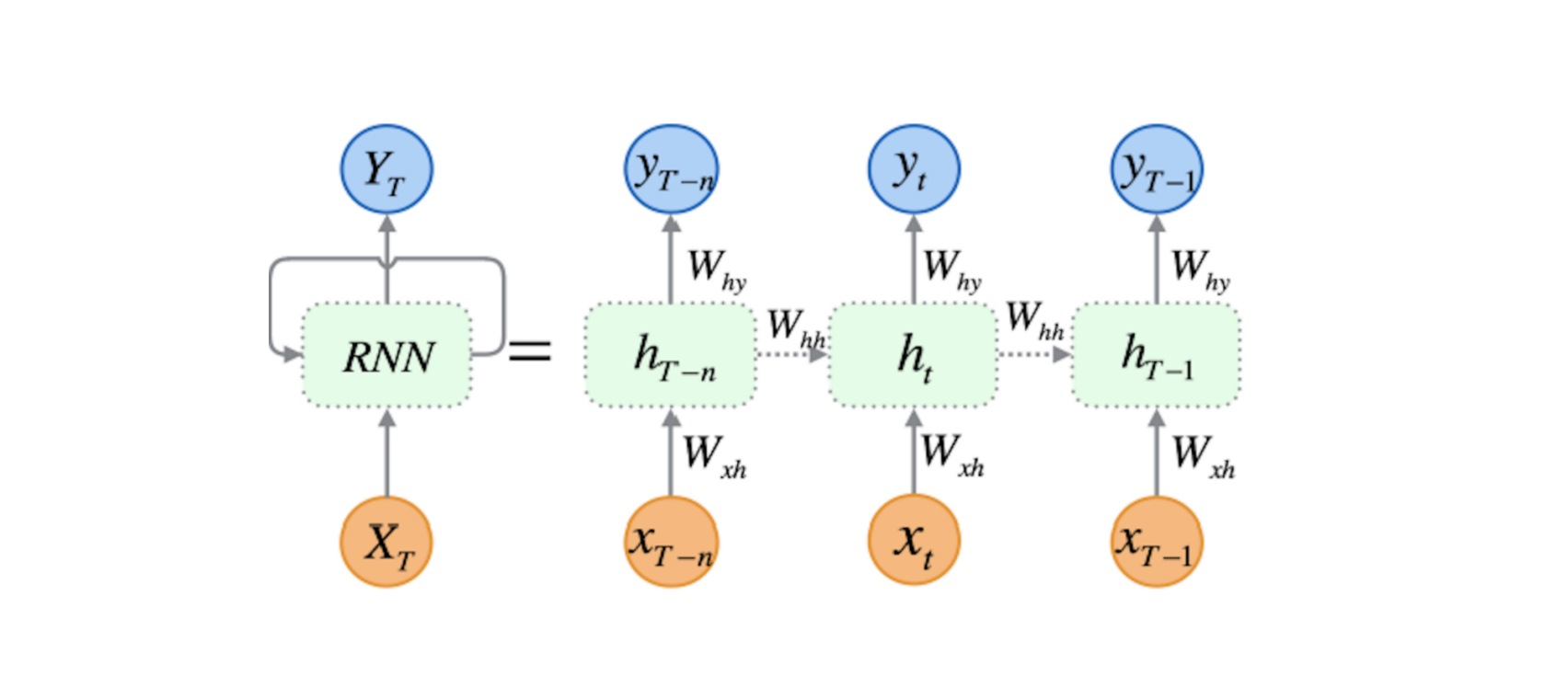
当然，由于纯RNN容易受梯度消失等因素影响，在实际操作中一般使用长短期记忆网络即LSTM对RNN进行一个替代，这里我们就不针对LSTM展开来讲了，对LSTM细节有兴趣的伙伴可以通过这个链接来了解下，这里我们可以把LSTM当做RNN的一个加强版来看待。
接下来我们需要的是利用这个循环神经网络来帮我们建立知识追踪的模型。我们要考虑的第一点是如何把学生的历史学习轨迹数据表示成循环网络可以接受的形式。这里面谈一个比较直接的表示方法，即 One-Hot Encoding（独热编码）。按上面介绍知识追踪时提到的，我们可以把xt表示成xt={qt,at}。假设我们要追踪 M 个不同的知识点，我们可以令 xt 是一个长度为 2M 的向量（向量的前 M 位描述学生做的题是哪一个知识点，后 M 位描述学生是否做对该知识点），其中量的可能取值可能是0或者1（如果学生做对第 k 个知识点，则第 k 位是1,第 M+k 也是1，其余是0；若学生做错第 k 个知识点，则仅有第 k 位为1，其余是0），则数学上 xt可以表示成 xt={0,1}2M，这样 xt就可以作为循环神经网络的输入了。而输出 yt 就是一个长度为 M 的连续向量了，其中第 k 位代表如果学生在t+1时刻做对第k个知识点的概率，所以我们从yt就可以判断当前学生在各个知识点上的掌握水平了。
至于训练的损失函数，我们就可以考虑使用经典的二值交叉熵。使用独热向量 δ(qt+1) 来表示在 t+1 时刻哪一个知识点会被回答，同时令 l 代表二值交叉熵函数。那么对一个学生而言损失函数便是:
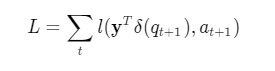
通俗来讲，比如我们在 t+1 时刻做了第 k 个知识点的题，我们就去找输出结果 yt 中对知识点 k 的预测值，然后把这个预测值与真正学生在第 t+1 时刻知识点 k 的作答结果 at+1进行对比，预测值越是接近这个真实的 at+1 则对应的损失值越小，反之则越大。我们的训练目标是使得最终的损失 L 最小，可以通过梯度下降的方式降低损失 L，从而达到对网络参数进行优化的目的，为了防止过拟合，也可以在训练中采取一些 dropout 等常用方式。
我们现在来看一下DKT训练好后的效果图（该图是针对一个学生而言）：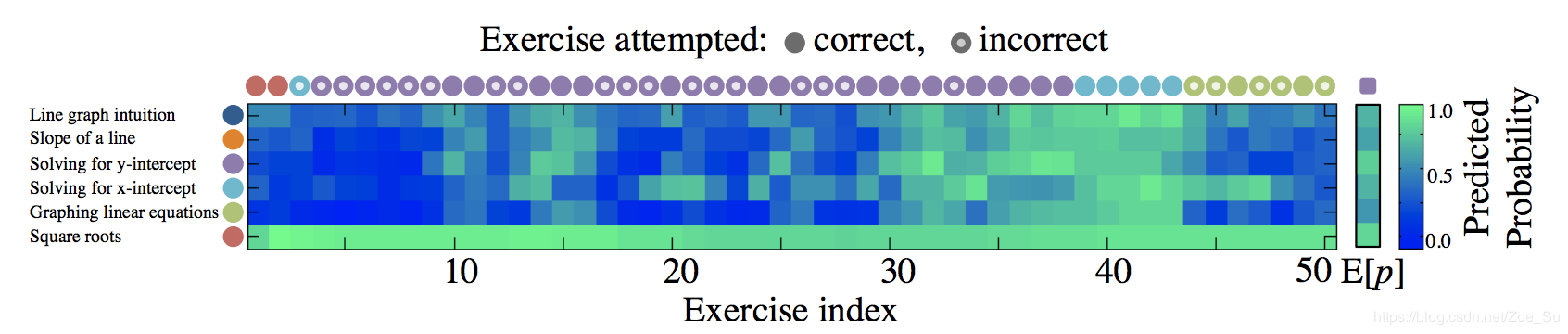
上图左边每个彩色圆圈我们可以看成不同的知识点，从图中可以获取我们要测试M=6 个不同的知识点的信息，横着的彩色圆圈代表学生在不同时刻真实做的题是什么样知识点的题以及回答情况，其中若圆圈是空心代表学生答错该题，而实心代表学生答对该题，矩形底下的数字代表该生回答到了第几题（即作答时间点,上图中学生历史共回答了50题）。而矩形中的第 t 列的6个方格颜色深浅代表每个作答时间点模型对学生6个知识点掌握的预测（越绿则代表掌握程度越高），即模型中的输出 yt。我们可以根据 yt 去预测 t+1时刻学生的作答表现，同时，yt也可以用来当做第t时刻学生知识点掌握熟练程度的描述。
训练知识追踪的目标是利用学生的历史学习数据去预测学生在未来的表现情况。如果深度知识追踪可以真的能达到理想的效果，我们便可以利用学生日常练习数据去判断一个学生现在的能力是怎么样的，那我们组织统一考试的必要性与频率就可以大大地降低了。
深度知识追踪最大的一个潜在应用是帮助学生优化知识点的学习效率，根据学生实时的知识点掌握水平来帮助学生选择最好的学习的顺序。比如 t 时刻学生在知识点A的掌握程度最差，即yt在知识点A对应的维度上的数值最低,则我们可以尝试提高为学生讲解A知识点的优先级，这样可以帮助学生有针对性补他目前知识上最大的短板。
DKT模型也可以用来发现不同知识点间的联系。对于知识点 i 和知识点 j 而言我们可以用 Jij 来代表两个知识点间的关联强度，
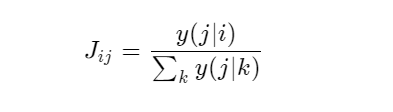
其中 y(j|i) 代表的意思是如果学生在此刻做对了知识点 i，他下一个时间点做对知识点 j 的概率，上面的式子通俗地可以理解成知识点 i 和知识点 j 的关系其实就是做完知识点 i 后做对知识点 j 的概率在所有做完知识点 k 然后再做对知识点 j 的概率的占比。因为如果知识点 i 和 知识点 j 的关系越紧密，则做完知识点 i 后做对知识点 j 的概率相比于做完其他知识点后再做对知识点 j 的概率来的相对较高，所以对应的 Jij 也会较高。这样我们就可以通过 J 的值来对两个知识点间的关系进行判断了。
相比贝叶斯知识追踪（BKT）深度知识追踪（DKT）有不少优势：
模型可以反映出长时间的知识掌握程度，相比传统贝BKT假设知识一旦掌握了就不再会被遗忘，深度知识追踪引入循环神经网络模型可以很好地模拟知识长时间不做会被遗忘的行为，更加符合人们的认知。
能够对复杂的知识点间的联系进行建模，从而发现不同知识点间的内在联系。
不同于BKT用0/1来表示学生知识点掌握状态，DKT输出的 yt 是连续值，DKT可以反映出学生连续的知识水平变化。
当然深度知识追踪模型也是存在着缺点的 [4]：
模型存在无法重构的可能性，比如学生在此刻做对 i 知识点，但是某些情况下，模型认为下一刻对 i 知识点的掌握水平反而下降。
在时间序列上，学生存在对知识点掌握程度不连续的情况，部分学生的波动可能过大。
上述两个缺点可以通过修改损失函数进行解决，已有相关的论文对深度知识追踪模型进行改良，提出了对应的解决方案，并获得精度上进一步提升，同时对上面缺点中提到的问题有了很好的提升与修复。
整体来说，深度知识追踪模型（DKT）可以作为一种人工智能手段自动发现知识点间相互关系同时可以智能设计学生学习路径达到提高学习效率的目的。DKT也是目前相应领域中相对前沿的模型，各种相关的DKT+也如雨后春笋般不断出现，大家可以对领域中新的研究多加关注，遇到相关问题也欢迎大家随时一起沟通讨论，让我们一起借模型和数据的力量为业务智能化打出更大的价值！
[1]. LIU Heng-yu, ZHANG Tian-cheng, WU Pei-wen, et al. A review of knowledge tracking[J]. Journal of East China Normal University (Natural Science), 2019, (5): 1-15. DOI: 10.3969/j.issn.1000-5641.2019.05.001.
[2]. Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L. J., & Sohl-Dickstein, J. (2015). Deep Knowledge Tracing. In Advances in Neural Information Processing Systems (pp. 505-513).
[3]. Z. Cui, R. Ke, and Y. Wang, “Deep Stacked Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction,” in 6th International Workshop on Urban Computing (UrbComp 2017), 2016.
[4]. Chun-Kit Yeung and Dit-Yan Yeung. Addressing two problems in deep knowledge tracing via predictionconsistent regularization. In Proceedings of the 5th ACM Conference on Learning @ Scale, pages 5:1–5:10. ACM, 2018.
标签：兴趣 hang 参数 对比 目标 drop mda tle ons
原文地址：https://www.cnblogs.com/vwvwvwgwg/p/12833451.html
