标签:次数 mit limit 因此 http 矩阵 变量 问题 详细
熵权法是一种在综合考虑各因素提供信息量的 基础上计算一个综合指标的数学方法。作为客观综合定权法,其主要根据各指标传递给决策者的信息量大小来确定权重。根据信息论基本原理,信息是系统有序程度的度量;而熵则是系统无序程度的度量。因此,可用系 统熵来反映其提供给决策者的信息量大小,系统熵可通过熵权法得到。
熵值法确定权重的基本步骤:
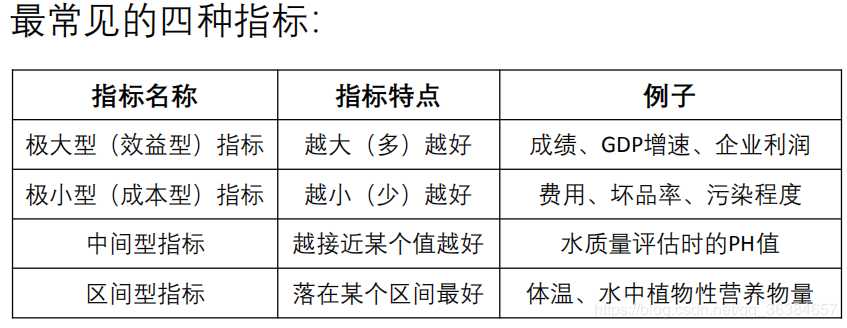
3.计算第j项指标下第i个样本占该指标的比重:
4.计算第j项指标的熵值:其中
. 满足
;
5.计算信息熵冗余度:
6.计算各项指标的权值:
7. 计算各样本的综合得分:
运行代码:
clc;clear; % 实现用熵值法求各指标(列)的权重及各数据行的得分 % x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标 % s返回各行得分, w返回各列权重 load(‘data_water_quality.mat‘)%载入数据 x=X; %X为工作表中的样本数据 %% 数据的正向化处理 [n,m]=size(x); % X中有n个样本, m个指标 disp([‘共有‘ num2str(n) ‘个评价对象, ‘ num2str(m) ‘个评价指标‘]) Judge = input([‘这‘ num2str(m) ‘个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0: ‘]); if Judge == 1 Position = input(‘请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: ‘); %[2,3,4] disp(‘请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ‘) Type = input(‘例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: ‘); %[2,1,3] % 注意,Position和Type是两个同维度的行向量 for i = 1 : size(Position,2) %这里需要对这些列分别处理,因此我们需要知道一共要处理的次数,即循环的次数 X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i)); % Positivization是我们自己定义的函数,其作用是进行正向化,其一共接收三个参数 % 第一个参数是要正向化处理的那一列向量 B(:,Position(i)) X(:,n)表示取第n列的全部元素 % 第二个参数是对应的这一列的指标类型(1:极小型, 2:中间型, 3:区间型) % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列 % 该函数有一个返回值,它返回正向化之后的指标,我们可以将其直接赋值给我们原始要处理的那一列向量 end disp(‘正向化后的矩阵 X = ‘) disp(X) end %% 数据的归一化处理 % Matlab2010b,2011a,b版本都有bug,需如下处理. 其它版本直接用[X,ps]=mapminmax(x‘,0,1);即可 [B,ps]=mapminmax(X‘); ps.ymin=0.002; % 归一化后的最小值 ps.ymax=0.996; % 归一化后的最大值 ps.yrange=ps.ymax-ps.ymin; % 归一化后的极差,若不调整该值, 则逆运算会出错 B=mapminmax(X‘,ps); % mapminmax(‘reverse‘,xx,ps); % 反归一化, 回到原数据 B=B‘; % B为归一化后的数据 %% 计算第j个指标下,第i个记录占该指标的比重p(i,j) for i=1:n for j=1:m p(i,j)=B(i,j)/sum(X(:,j)); end end %% 计算第j个指标的熵值e(j) k=1/log(n); for j=1:m e(j)=-k*sum(p(:,j).*log(p(:,j))); end d=ones(1,m)-e; % 计算信息熵冗余度 w=d./sum(d); % 求权值w s=w*p‘; % 求综合得分[\code] disp("信息冗余度为");disp(d) disp("各样本综合得分s为");disp(s); disp("各指标权重w为");disp(w);
正向化函数代码
(1)Positivization
% function [输出变量] = 函数名称(输入变量) % 函数的中间部分都是函数体 % 函数的最后要用end结尾 % 输出变量和输入变量可以有多个,用逗号隔开 % function [a,b,c]=test(d,e,f) % a=d+e; % b=e+f; % c=f+d; % end % 自定义的函数要单独放在一个m文件中,不可以直接放在主函数里面(和其他大多数语言不同) function [posit_x] = Positivization(x,type,i) % 输入变量有三个: % x:需要正向化处理的指标对应的原始列向量 % type: 指标的类型(1:极小型, 2:中间型, 3:区间型) % i: 正在处理的是原始矩阵中的哪一列 % 输出变量posit_x表示:正向化后的列向量 if type == 1 %极小型 disp([‘第‘ num2str(i) ‘列是极小型,正在正向化‘] ) posit_x = Min2Max(x); %调用Min2Max函数来正向化 disp([‘第‘ num2str(i) ‘列极小型正向化处理完成‘] ) disp(‘~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~‘) elseif type == 2 %中间型 disp([‘第‘ num2str(i) ‘列是中间型‘] ) best = input(‘请输入最佳的那一个值: ‘); posit_x = Mid2Max(x,best); disp([‘第‘ num2str(i) ‘列中间型正向化处理完成‘] ) disp(‘~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~‘) elseif type == 3 %区间型 disp([‘第‘ num2str(i) ‘列是区间型‘] ) a = input(‘请输入区间的下界: ‘); b = input(‘请输入区间的上界: ‘); posit_x = Inter2Max(x,a,b); disp([‘第‘ num2str(i) ‘列区间型正向化处理完成‘] ) disp(‘~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~‘) else disp(‘没有这种类型的指标,请检查Type向量中是否有除了1、2、3之外的其他值‘) end end
(2)Inter2Max
function [posit_x] = Inter2Max(x,a,b) r_x = size(x,1); % row of x M = max([a-min(x),max(x)-b]); posit_x = zeros(r_x,1); %zeros函数用法: zeros(3) zeros(3,1) ones(3) % 初始化posit_x全为0 初始化的目的是节省处理时间 for i = 1: r_x if x(i) < a posit_x(i) = 1-(a-x(i))/M; elseif x(i) > b posit_x(i) = 1-(x(i)-b)/M; else posit_x(i) = 1; end end end
(3)Mid2Max
function [posit_x] = Mid2Max(x,best) M = max(abs(x-best)); posit_x = 1 - abs(x-best) / M; end
(4)Min2Max
function [posit_x] = Min2Max(x) posit_x = max(x) - x; %posit_x = 1 ./ x; %如果x全部都大于0,也可以这样正向化 end
运行结果如下图所示:
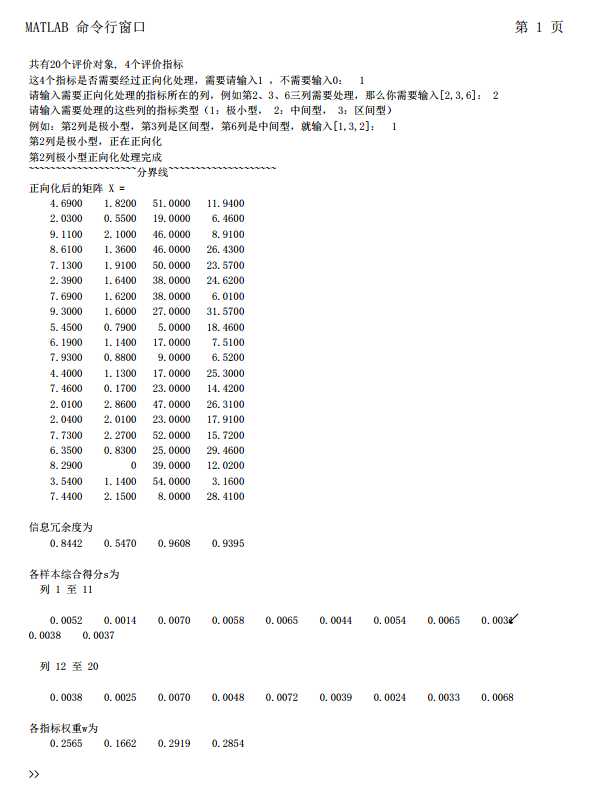
标签:次数 mit limit 因此 http 矩阵 变量 问题 详细
原文地址:https://www.cnblogs.com/Eudemonia8023/p/12835572.html