标签:int 序列 parse als ida 转移 ali 可能性 lock
2.阅读代码——动态规划
乔治·桑塔亚纳说过,“那些遗忘过去的人注定要重蹈覆辙。”这句话放在问题求解过程中也同样适用。不懂动态规划的人会在解决过的问题上再次浪费时间,懂的人则会事半功倍。那么什么是动态规划?这种算法有何神奇之处?
目的:为了避免解决重复性问题
void fun(int n)
{
if(n==0)
return 0;
if(n==1)
return 1;
reurn fun(n-2)+fun(n-1);
}
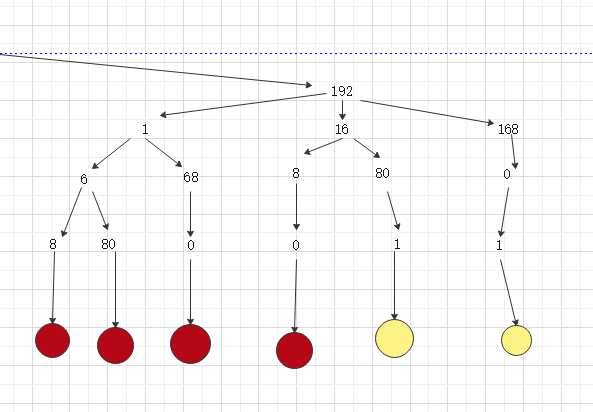
任何一个递归函数,都可以化成一棵树。
如图所示:
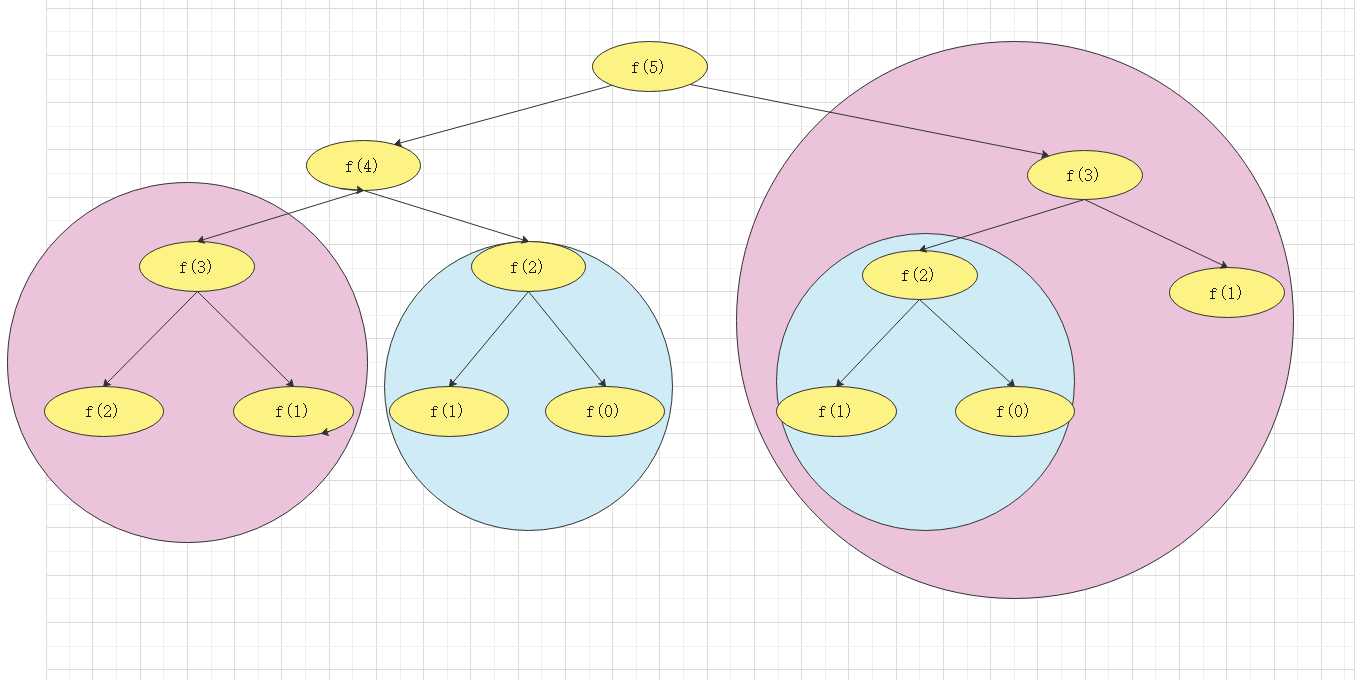
从图片上可以看到,以粉色为底的第二层f(3)同样在第三层也重复算了一遍,第三层的f(2)重复算了两遍,第四层也有f(2),这样的问题,我们叫做重复子问题,由于重复计算同一个值的斐波那契值,致使递归的效率不高,所以我们引进动态规划。
把原问题分解成若干个子问题进行求解,先求解子问题,然后从这些子问题得到原问题的姐解,不同的是,动态规划保存已解决的子问题的答案,便于在后面需要时能够马上得到,就可以节省大量的重复计算。
在动态规划里,有一个特别重要的角色,就是数组。而数组有一维数组和二维数组,至于是一维数组的选定还是二维数组的选定,要根据具体问题具体分析,一般二维数组解决较难的题目,讲到这里,其实还没有对动态规划形成一个具体的概念,请看下面的典型应用,加深理解。
斐波那契数列:
int fun(int x)
{
int dp[max];
dp[0]=0;dp[1]=1;dp[2]=1;
for(int i=3;i<=x;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[x];
}
从上面就可以发现,如果当数据量急剧增大时,递归和动态规划的的效率也会有明显差异。
这里有一个小技巧,运用dp时,我们想要的得到的结果一般是数组的最后一个,例如我们求斐波那契值时,就是一维数组的最后最后一位,如果是二维数组,那么结果则是位于最右下角的那一位
题意分析:
图解:
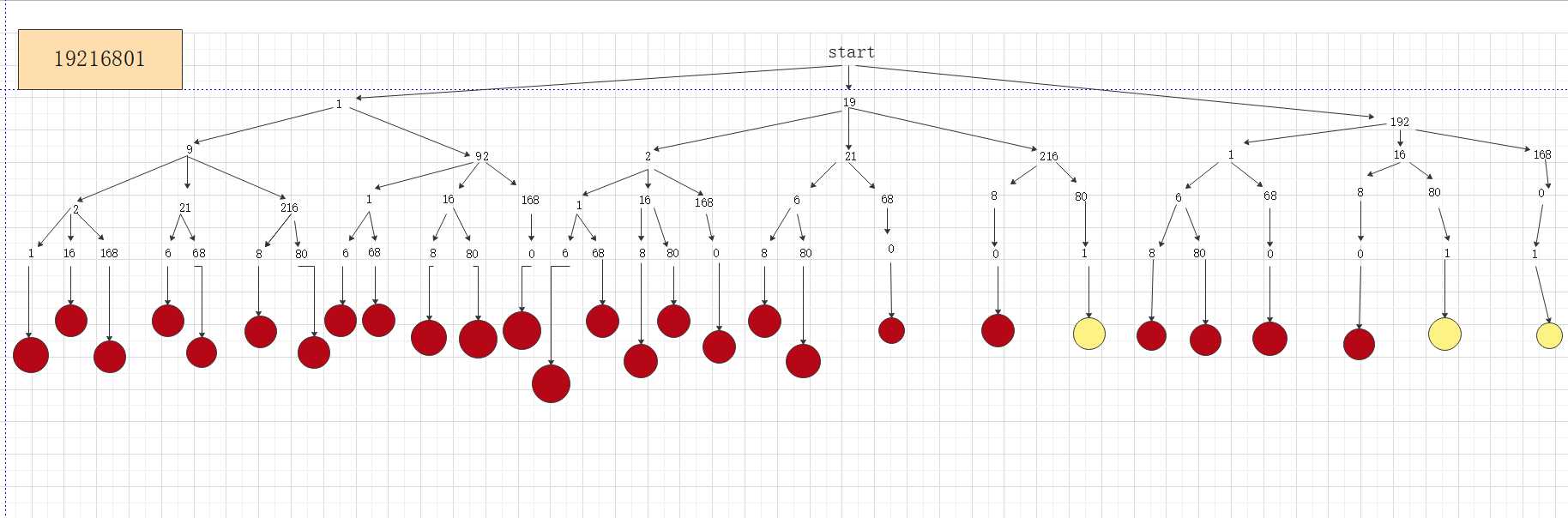
具体部分:
图一:
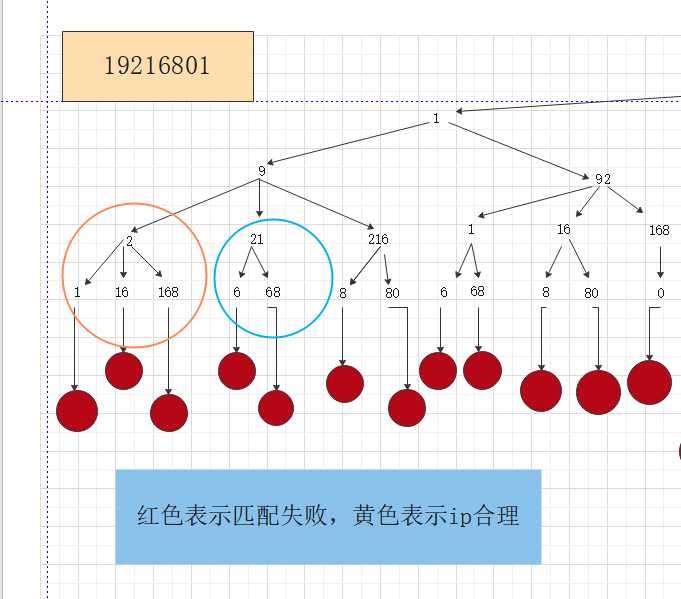
图二:
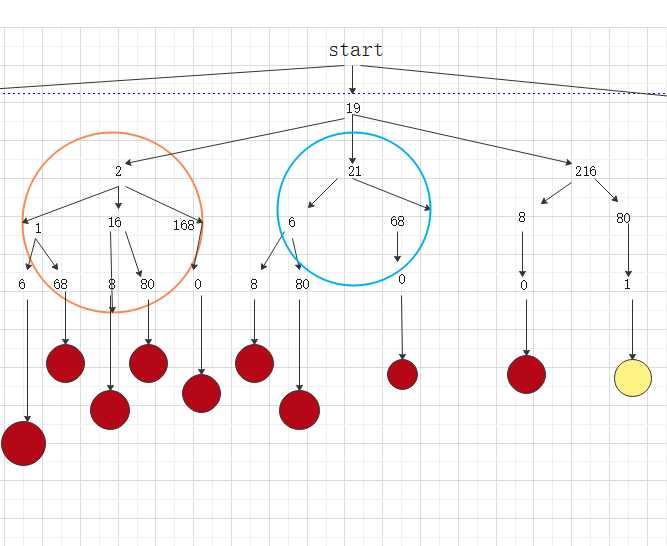
图三:
由图一和图二的橙色圈圈和蓝色圈圈可知,则这道题画成一棵树,则会出现很多的重复子问题,那么用动态规划的图如下,这道题,要选择二维dp数组作为载体,来存放已解决的子问题。
画图注意点:
动态规划图解分解过程:
第一步:对d[i] [j]数组进行初始化,对i和j等于0的地方,可赋值为0,因为没有意义;
比如i=0时,j=1时,表示1可以表示0个255的方法有几种,显然没意义,所以直接赋值为0;
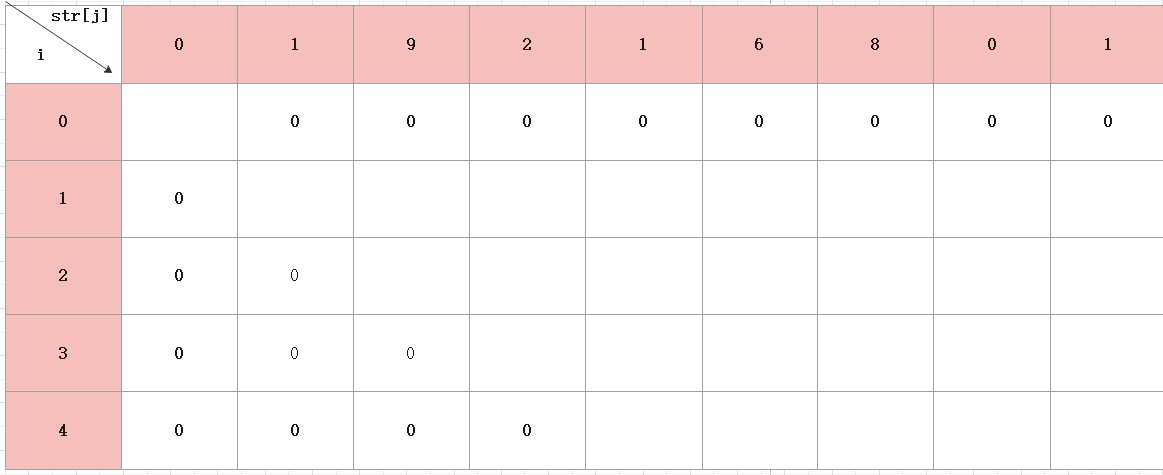
第二步:对i=1开始分析。
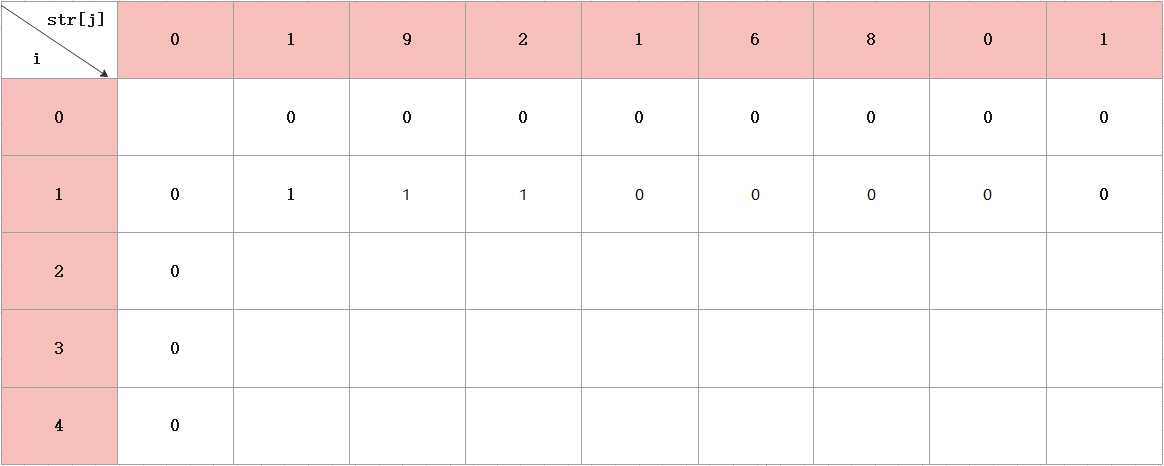
第三步:从i=2开始分析
由前面可知,j=1时,根据意义,1不能表示2个255以内的数,所以是0
j=1时,要注意,从i=2开始后,不是直接看19是255以内的数,那它就是一种,这种想法是错误的,对于递归问题转动态规划,我们要看它的起源,所以j=2,先看9是不是255以内的数,则应该返回i=1那一行看,如果9是,则d[2] [2]+=d[1] [1],然后再看19是不是255以内的数,如果是,则d[2] [2]+=d[1] [0],所以最终d[2] [2]=1.
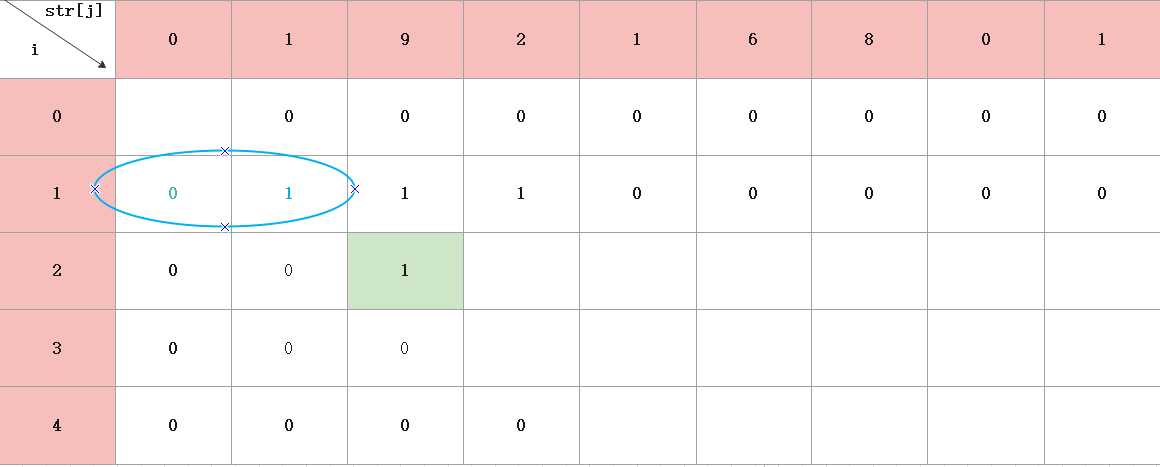
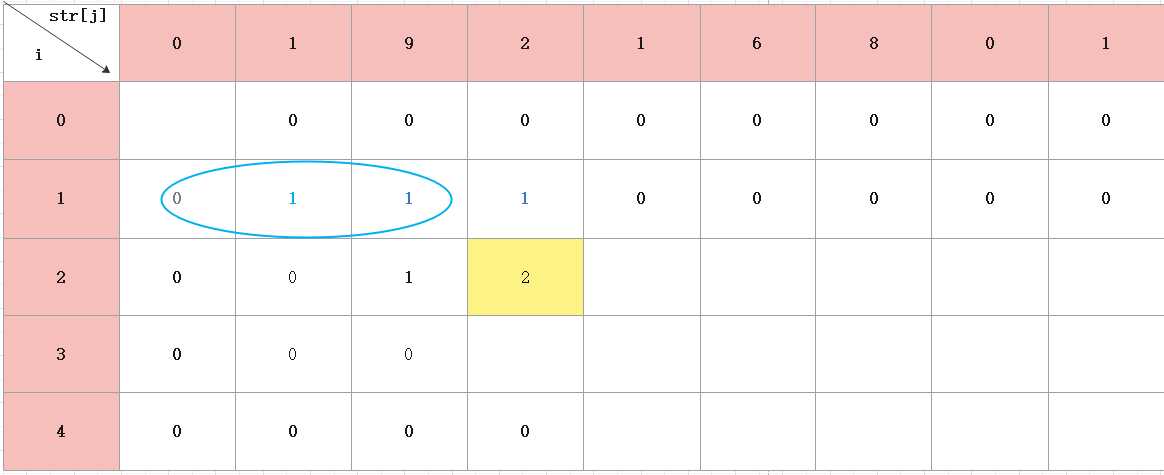
d[2] [3]+=dp[1] [1],看192是不是255以内的数,如果是d[2] [3]+=dp[1] [0]。最终,d[2] [3]=2。
同理,后面的数,也是这样得出。经过多次运算,我们会发现一种规律,每一个格子的值都是当前格子左上角的三个格子之和组成,那为什么是三个格子,也不一定,看具体要求,因为这道题是不超过255,那肯定只能是三位数,所以就是三个格子。最后,组成的图如下:
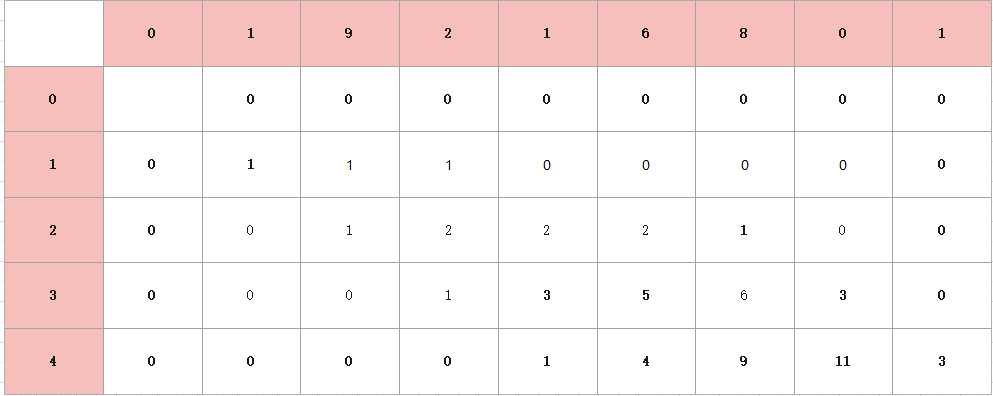
那么我们会有一个疑问,为什么最后的答案就是我们要求。这需要我们回归树形图。拿其中一个格子来说。
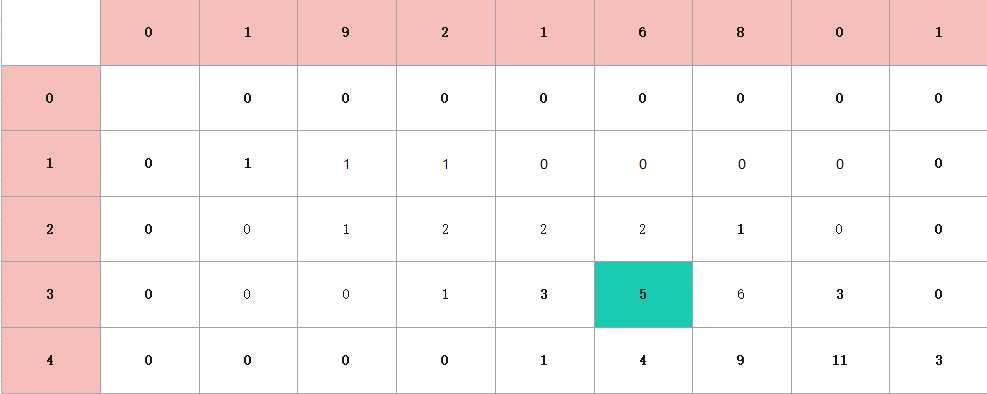
为什么这个格子是5?
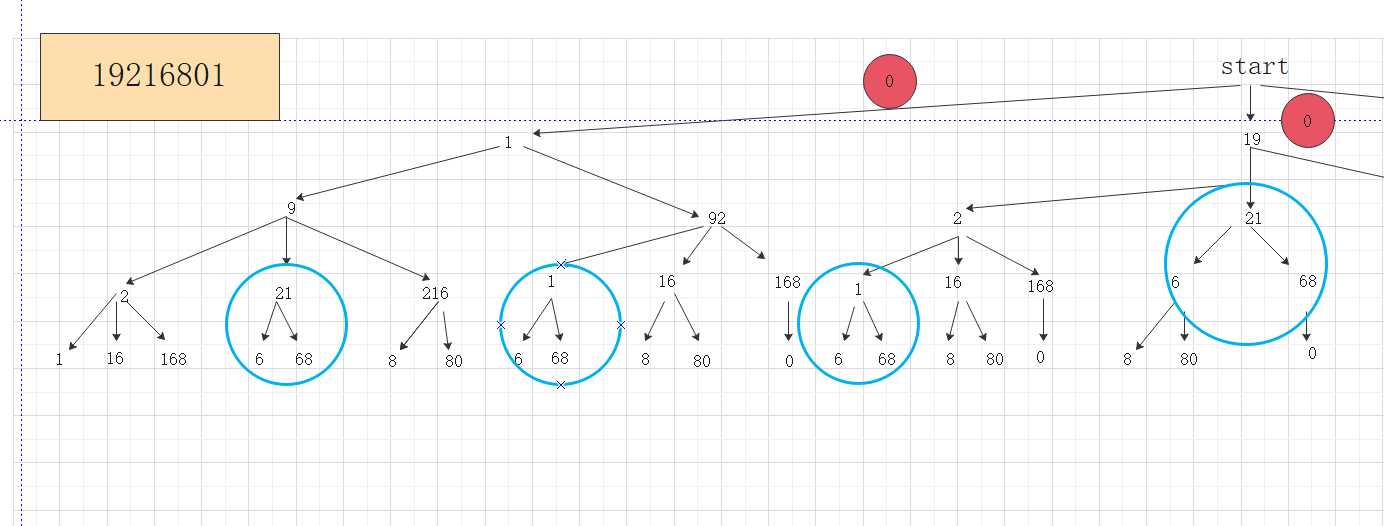
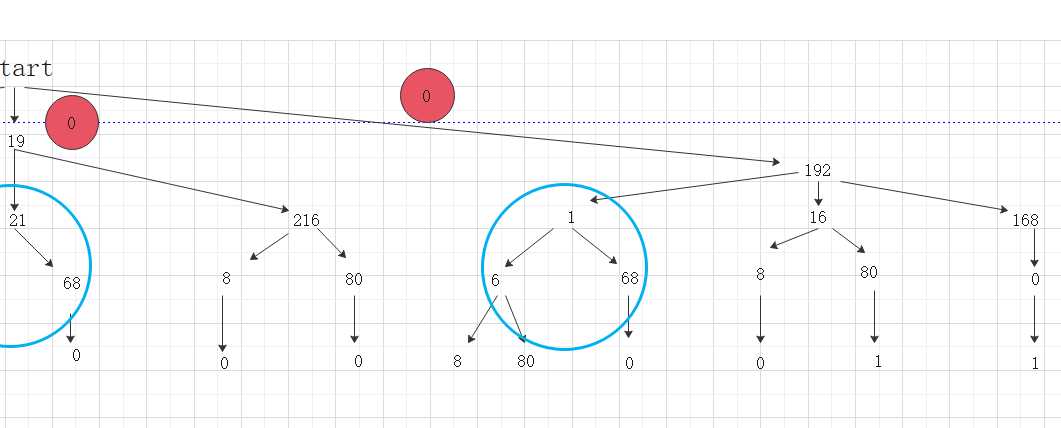
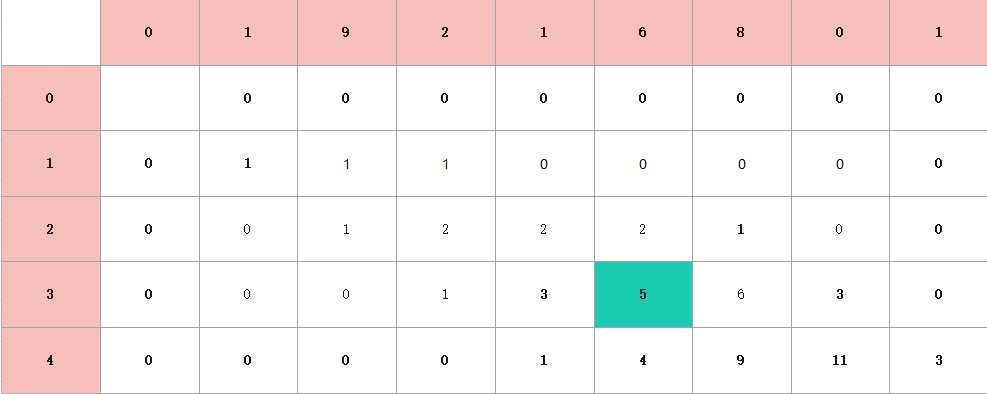
仔细数数,图中蓝色的圈圈是否有5个,就说明6的起源有5个,再回归方格图,我们就会有一种感觉,如果看的是dp[3] [1]=3这个数,我们就可以去树形图里找1的起源,会有三个圈,而1所在的树的层次肯定会比6的层次高,因为1在前面,所以1会是6的子问题,所以,这棵树,与这个表结合,表从上到下的子问题的答案,到最后,我们要求的答案,而树,从上到下,每一个分支,也是一个子问题,到叶子节点,可能就是我们要找的答案。
接下来,我们来看代码实现。
int DP(string str)
{
int len=str.length;
int dp[5][len+1]={0};
//进行初始化
for(int i=0;i<5;i++)//先对dp数组进行遍历赋值
{
for(int j=i;j<len;j++)
{
if(i==0&&j==0)//dp[0][0]置为1,后面比较好算
{
dp[i][j]=1;
continue;
}
if(i==0)//第一行没有意义,所以为0
{
dp[i][j]=0;
continue;
}
dp[i][j]=0;
for(int x=1;x<=3;x++)//三位数
{
if(j-x>=0&&validate(str.substr(j-x+1,x)))
//str.substr(a,b),表示从j-x+1这个地方开始截取x个字符
//validate()这个函数是判断数字
{
dp[i][j]+=dp[i-1][j-x];
}
}
}
}
return dp[4][len]
};
int validate(string str)
{
if(s==‘0‘) return true;
if(s.startWith(‘0‘)) return false;
return parseInt(s)<=255;
}
/*
库函数
str.startWith(ch) //判断字符串是否以‘0’开头
parseInt(str) //是将str字符串转化为数字的函数
*/
int DP(string str)
{
得到字符串的长度len
申请多一个空间的dp数组,并初始化
for i=0 to i=4//对dp数组进行遍历
{
for j=i to j=len-1
{
if(i==0&&j==0)//dp[0][0]置为1,后面比较好算,不影响之前的分析
{
dp[i][j]=1;
continue;
}
if(如果是第一行)
{
没有意义,则dp[i][j]=0;
continue;
}
dp[i][j]=0;
for x=1 to x=3 //三位数
{
if(从j-x+1这个地方开始截取x字符,并且数字有意义)
{
dp[i][j]+=dp[i-1][j-x];
}
}
}
}
}
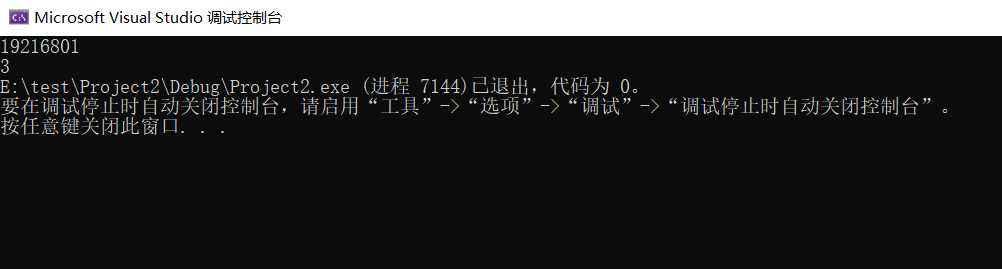
对于上面这道题,其实也可以通过递归来实现,根据一些前辈的经验,得出了两个经验,一是只要遇到字符串的子序列或配准问题首先考虑动态规划DP, 二是只要遇到需要求出所有可能情况首先考虑用递归,但是上面这道题目,其实用动态规划也可以理解。
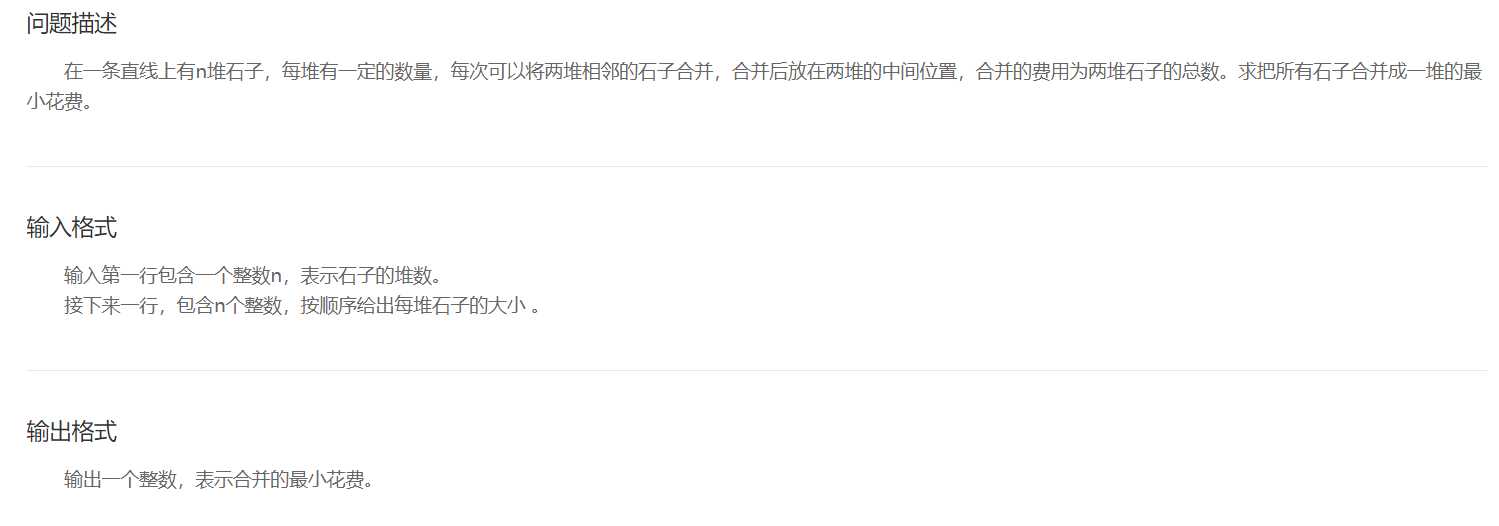
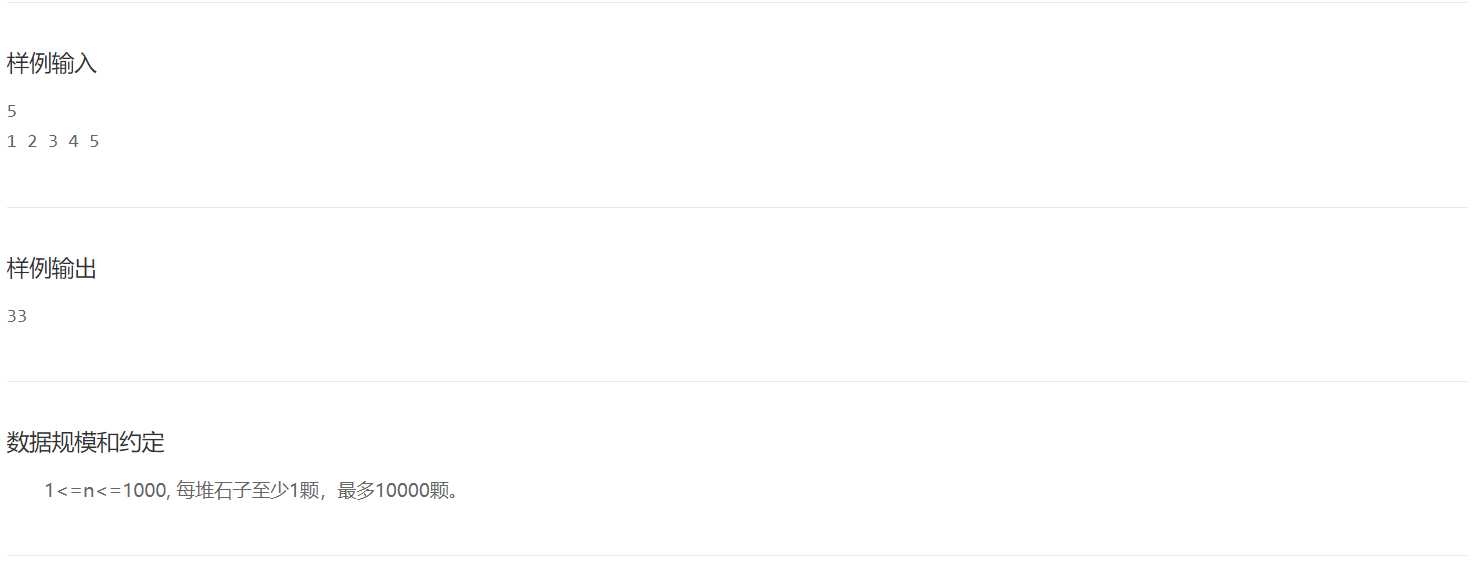
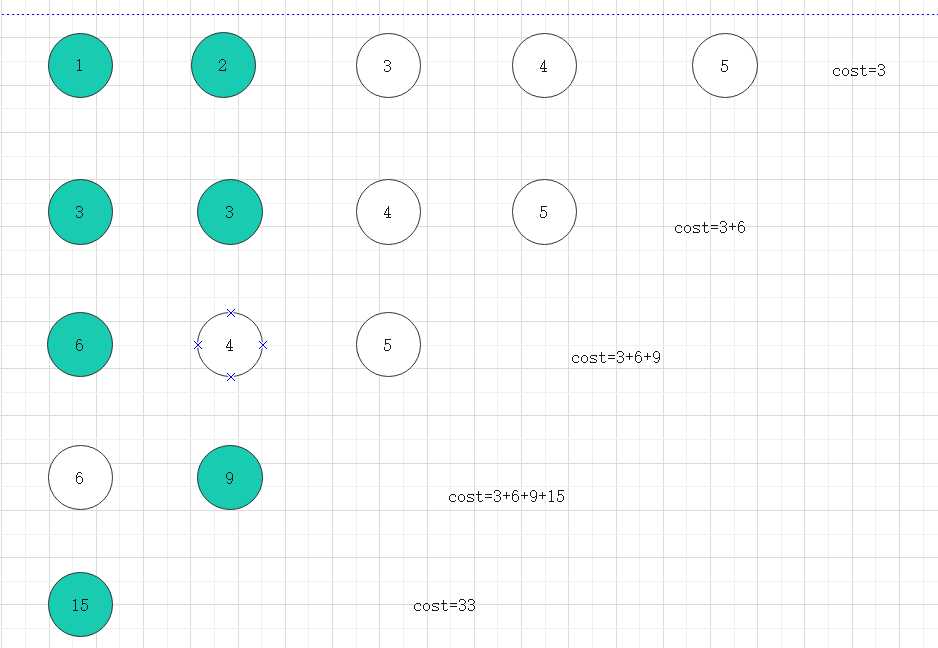
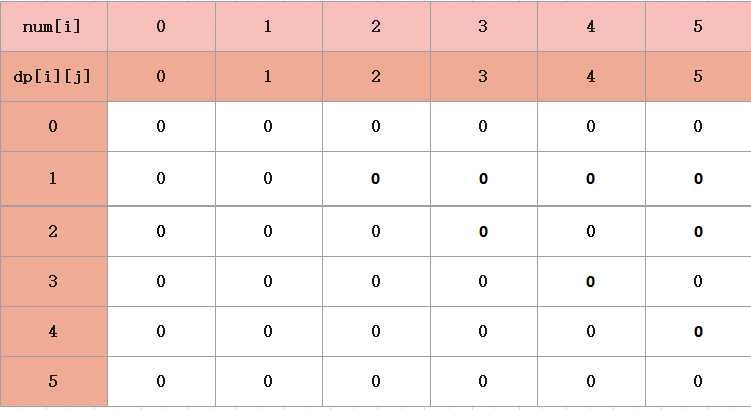
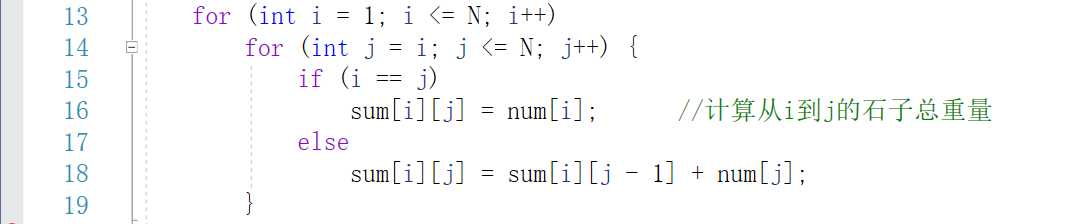
上面的步骤,其实只是对这些石子所有可能性进行一个存储,所以,接下来,要进入核心代码的部分,真正进行dp[] []数组的操作。

for i=1 to i=N
for j=i to j=N
计算把第i堆合并到第j堆需要的费用
用sum数组存储
for j=2 to j=N
{
for i=j to j=0
{
先对dp[i][j]初始化为无穷大
for k=i to k=j-1
{
从i到j共有j-i个状态,取最优值
dp[i][j]=min(dp[i][j],dp[i] [k]+dp[k+1][j]+sum[i][j]);
}
}
}
DP过程:
以归并石子的长度为阶段,一共有n-1个阶段
状态:每个阶段有多少堆石子要归并
当归并长度为2时,有n-1个状态,分别为1和2合并,2和3合并.....n-1和n合并
当归并长度为3时,有n-2个状态,分别为1,2,3合并,2,3,4合并.....
当归并长度为n时,有1个状态
让我们看看上面的代码:
j=2,i=1
j=3,i=2
j=3,i=1
j=4,i=3
j=4,i=2
j=4,i=1
从上面的变化,其实我们可以看到,代码在算从i到j分别算出合并两个,三个,,这样算下去,含义就是从第i堆到第j堆,算出不同状态下的dp值
首先,对dp[i] [j]进行初始化。
对于动态规划,我们要知道,最核心的部分,就是能够找到dp[i] [j]横坐标,纵坐标表示的含义。
对于此题,dp[i] [j]表示的含义其中一种是就是从第i堆合并到第j堆的最小代价。
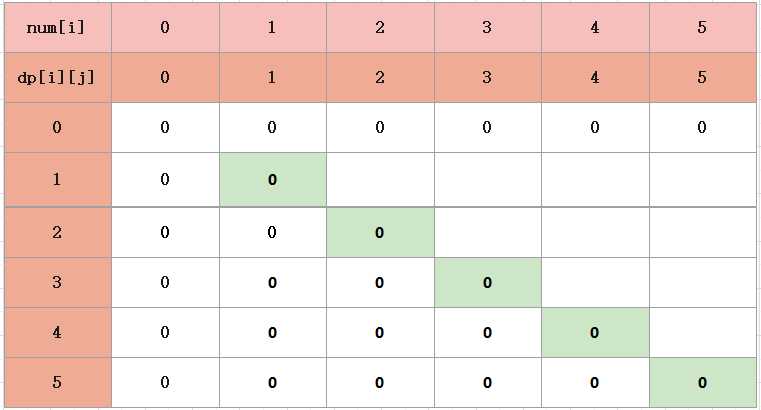
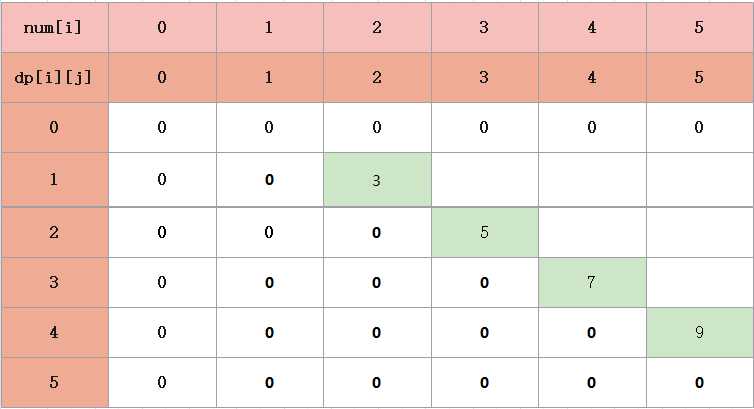
最后
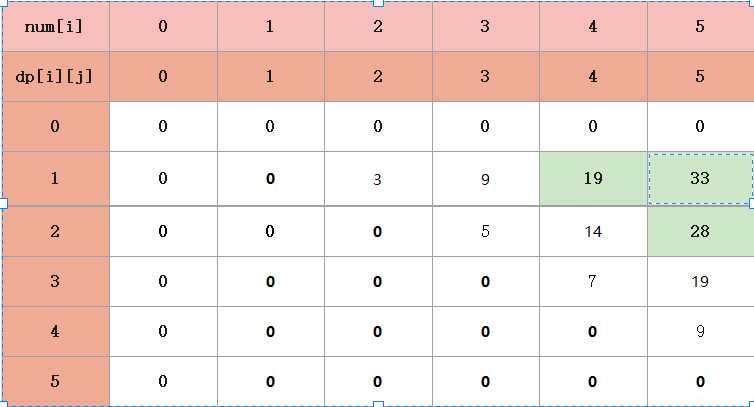
我们来举个例子吧
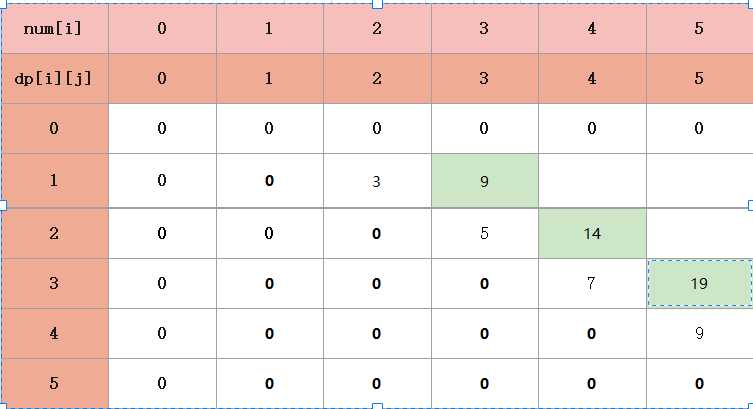
看表里的i=2,j=4,结合代码,含义是把第二堆第三堆第四堆进行合并
k=2时,dp[2] [2]+dp[3] [4]+sum[2] [4]
k=3时,dp[2] [3]+dp[4] [4]+sum[2] [4]
从上面就可看到,dp[2] [4]有两种选择,第三堆和第四堆先合并,再和第二堆进行合并,或者第二堆和第三堆先合并,再合并第四堆,然后比较它们之间的大小,就可以求出正解
这次我选的题目都是关于动态规划的,所有优势大都差不多,就不说了,动态规划的题目看多了,我觉得这道题给我的感觉就更多是枚举的感觉,通过二维数组来存储,其实,也是这道题让我写了这个全部都是动态规划的题目,因为一开始还不懂什么是动态规划,就碰上了这个题目,当时在那边死命的看这道题的题解,就是死命的看不懂,那在这之前,其实对动态规划有所耳闻,只是并没有非常认真地了解过,所以,就打算多找几道题,让我熟悉一下它
环形结构,经常采用双倍长度线性化的手段,也就是说,把环形结构看成是长度为环的两倍的两倍的线性结构来处理,将环化成线性结构
环的长度是N,所以题目相当于与有一排石子,1,,,,N,N+1,,,2N,然后就可以用线性的石子合并问题的方法做了
有个地方需要注意,f(i,j)总是和f(N+i,N+j)相等,所以可以减少一些不必要的计算。
将N结构的线性表,转换成双倍的2N结构的长度。然后在2N长度的表中,截取我们需要的长度N的部分就可以了
状态:
dp[i] [j]表示从第i堆合并到第j堆(合并成一堆)的最小代价
sum[i]表示前i堆石子的和
状态转移方程:
dp[i] [j]=min(dp[i] [k]+dp[(i+k+1)%n] [j-k-1]+sum[i] [j])(0<k<=j-1)(j<=k<j)
dp过程:
根据上面,就可以知道说,转换成线性结构后,和题目二是差不多的
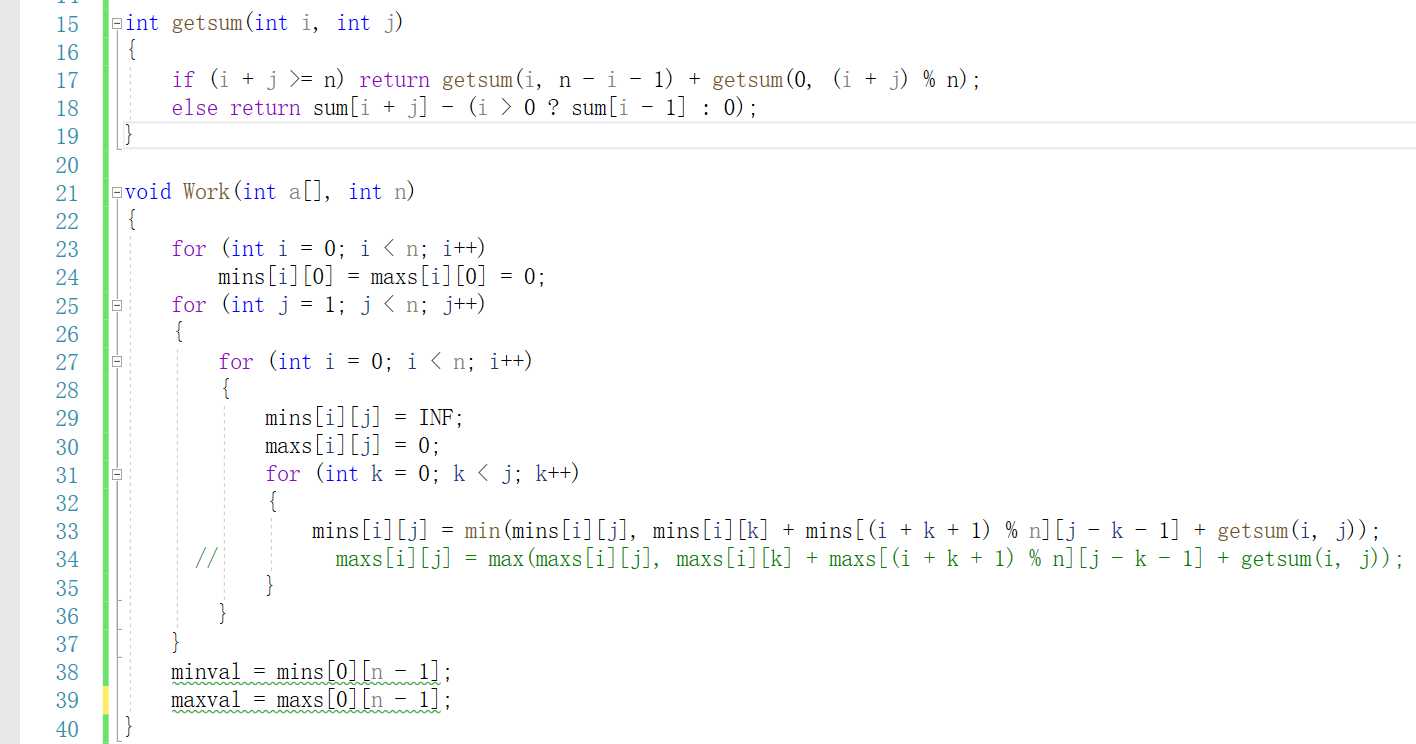

for i=1 to i=N
for j=i to j=N
计算把第i堆合并到第j堆需要的费用
用sum数组存储
for j=1 to j=n-1
for i=0 to i=n-1
{
对mins[i][j]初始化为无穷大
for k=0 k=j-1
{
计算从i到j共有j-i个状态,取最优值
}
}
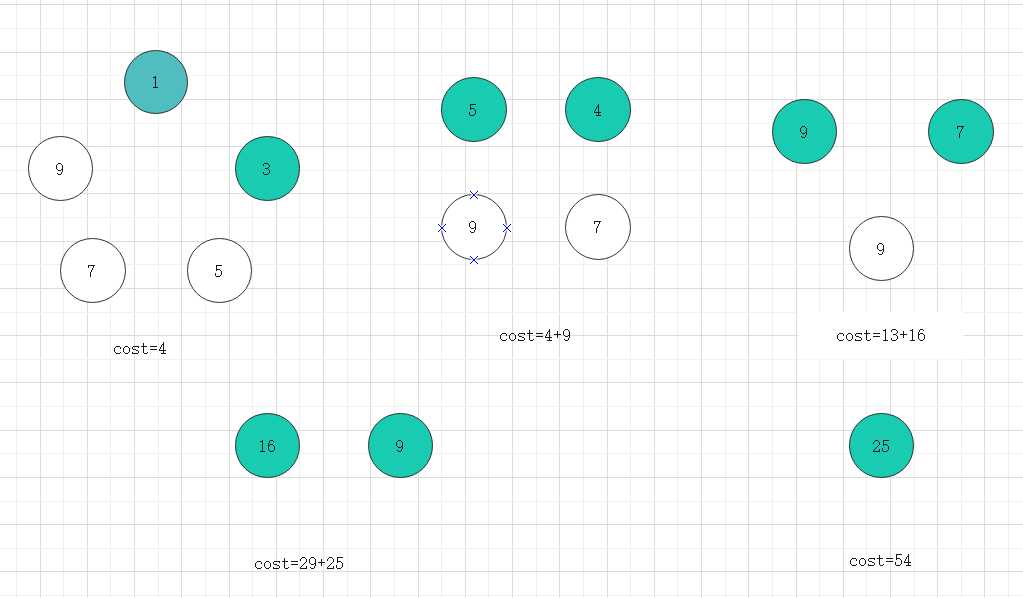

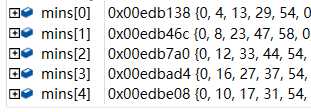
这个是用vs调试出来的结果
下面,对上面的数据进行分析
其实会发现,这题看多了,到最后一道题,再看的时候,就没那么难了,这最后一道题,我觉得最重要的是懂得环路处理起来的思路,其实想想我们上学期学过的数组左移右移这样,也是可以通过求余来算的,我上次看过一个视频,对于程序员,如何高效刷题,他说的是,对于同一类的题目应该给他刷个十几二十题的,并且可以有小本本记录下每一个超级经典,自己又容易错的,同样的题目看多了,遇到面试官的那些奇葩题目,都是万变不离其宗,也就不会慌了。
标签:int 序列 parse als ida 转移 ali 可能性 lock
原文地址:https://www.cnblogs.com/-sushi/p/12749595.html