CF-234 F. Fence DP

标签：force   names   红色   题意   include   int   inpu   name   class   

F. Fence

这个刷Fence的问题看到好几个了。。。

题意

有一个栅栏，由n块宽为1cm的木板组成，第i块木板高为h_i，要给他们刷上油漆，有一桶红色的可以刷a平方厘米的油漆，一桶绿色的可以刷b平方厘米的油漆。每块木板只能刷一种油漆。

现在要求出栅栏的不吸引值最小，定义不吸引值：相邻的木板不同颜色的接触长度。

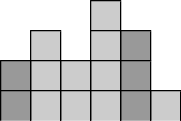
上图的不吸引人值为2+3+1=6.

如果无法刷完输出-1。

思路

dp[i][j][0]表示前i块木板用了j平方的红色油漆，第i块为红色油漆

dp[i][j][1]表示前i块木板用了j平方的红色油漆，第i块为绿色油漆

首先判断第i块是否可以为红色或者绿色

转移的时候判断第i块木板和第i-1块木板的颜色加上产生的不吸引值即可。

代码

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
const int N=4e4+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;

int n,a,b,arr[N],dp[210][N][2];
int sum[210];
/*
dp[i][j][k]表示前i块总共使用了j平方red最后颜色为k的最小不吸引值
*/
int main()
{
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    scanf("%d%d%d",&n,&a,&b);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&arr[i]);
        sum[i]=sum[i-1]+arr[i];
    }
    memset(dp,inf,sizeof(dp));
    dp[0][0][0]=dp[0][0][1]=0;
    for(int i=1; i<=n; i++)
    {
        for(int j=0; j<=a; j++)
        {
            /*
            最后一块可以使用red
            red的总量大于当前木板的面积
            red总量-当前木板面积+green总量>=前i-1块木板的面积和
            */
            if(j>=arr[i]&&(j-arr[i]+b)>=sum[i-1])
            {
                dp[i][j][0]=min(dp[i][j][0],dp[i-1][j-arr[i]][0]);//颜色相同，不吸引值为0
                dp[i][j][0]=min(dp[i][j][0],dp[i-1][j-arr[i]][1]+min(arr[i-1],arr[i]));//颜色不同，加上接触长度
            }
            /*
            最后一块可以使用green
            green总量大于当前木板的面积
            green总量-当前木板面积+使用a的量>=前i-1块木板的面积和
            */
            if(b>=arr[i]&&(b-arr[i]+j)>=sum[i-1])
            {
                dp[i][j][1]=min(dp[i][j][1],dp[i-1][j][1]);
                dp[i][j][1]=min(dp[i][j][1],dp[i-1][j][0]+min(arr[i-1],arr[i]));
            }
        }
    }
    int ans=inf;
    for(int i=0; i<=a; i++)
    {
        ans=min(ans,dp[n][i][0]);
        ans=min(ans,dp[n][i][1]);
    }
    if(ans==inf) printf("-1");
    else printf("%d\n",ans);
    return 0;
}

博客

CF-234 F. Fence DP

标签：force   names   红色   题意   include   int   inpu   name   class   

原文地址：https://www.cnblogs.com/valk3/p/12837225.html