标签:img 解码 pre using 赫夫曼编码 size 计算 tar 有序
赫夫曼树
最优二叉树,WPL值最小(效率最高);
利用结点的权重规划二叉树(权重大表示访问频繁),遍历二叉树的时让这些权重大的尽量早的被遍历到;有效的提高了遍历二叉树访问结点的效率
例如:判断成绩优,良,差;根据成绩分布情况规划最优判断结构树
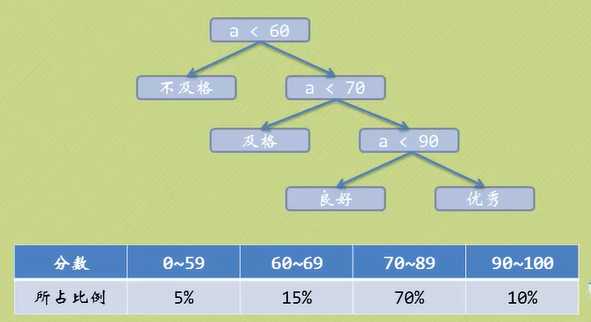
根据赫夫曼树的定义,可以计算出未规划的二叉树:WPL=5+15*2+70*3+10*3=275
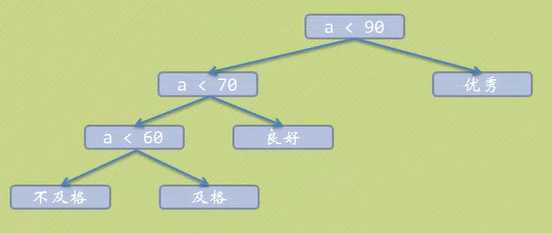
规划后WPL=10+70*2+15*3+5*3=210
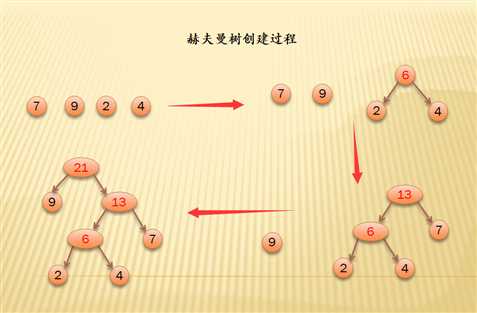
构造赫夫曼树的过程:
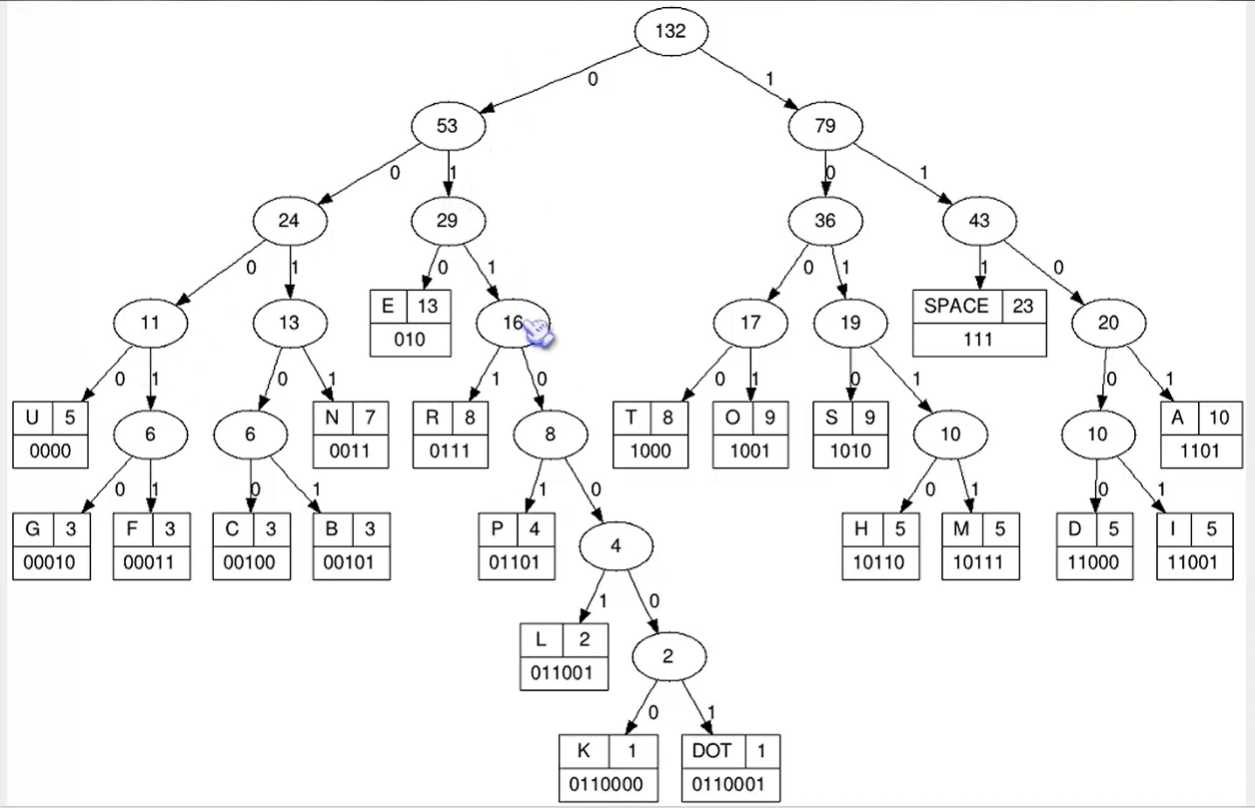
赫夫曼编码
可以有效的压缩数据,节省20%到90%的空间;
过程
1 #include<iostream> 2 #include<string> 3 using namespace std; 4 5 struct Node 6 { 7 double weight; 8 string ch; 9 string code; 10 int lchild, rchild, parent; 11 }; 12 13 void Select(Node huffTree[], int *a, int *b, int n)//找权值最小的两个a和b 14 { 15 int i; 16 double weight = 0; //找最小的数 17 for (i = 0; i <n; i++) 18 { 19 if (huffTree[i].parent != -1) //判断节点是否已经选过 20 continue; 21 else 22 { 23 if (weight == 0) 24 { 25 weight = huffTree[i].weight; 26 *a = i; 27 } 28 else 29 { 30 if (huffTree[i].weight < weight) 31 { 32 weight = huffTree[i].weight; 33 *a = i; 34 } 35 } 36 } 37 } 38 weight = 0; //找第二小的数 39 for (i = 0; i < n; i++) 40 { 41 if (huffTree[i].parent != -1 || (i == *a))//排除已选过的数 42 continue; 43 else 44 { 45 if (weight == 0) 46 { 47 weight = huffTree[i].weight; 48 *b = i; 49 } 50 else 51 { 52 if (huffTree[i].weight < weight) 53 { 54 weight = huffTree[i].weight; 55 *b = i; 56 } 57 } 58 } 59 } 60 int temp; 61 if (huffTree[*a].lchild < huffTree[*b].lchild) //小的数放左边 62 { 63 temp = *a; 64 *a = *b; 65 *b = temp; 66 } 67 } 68 69 void Huff_Tree(Node huffTree[], int w[], string ch[], int n) 70 { 71 for (int i = 0; i < 2 * n - 1; i++) //初始过程 72 { 73 huffTree[i].parent = -1; 74 huffTree[i].lchild = -1; 75 huffTree[i].rchild = -1; 76 huffTree[i].code = ""; 77 } 78 for (int i = 0; i < n; i++) 79 { 80 huffTree[i].weight = w[i]; 81 huffTree[i].ch = ch[i]; 82 } 83 for (int k = n; k < 2 * n - 1; k++) 84 { 85 int i1 = 0; 86 int i2 = 0; 87 Select(huffTree, &i1, &i2, k); //将i1,i2节点合成节点k 88 huffTree[i1].parent = k; 89 huffTree[i2].parent = k; 90 huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight; 91 huffTree[k].lchild = i1; 92 huffTree[k].rchild = i2; 93 } 94 } 95 96 void Huff_Code(Node huffTree[], int n) 97 { 98 int i, j, k; 99 string s = ""; 100 for (i = 0; i < n; i++) 101 { 102 s = ""; 103 j = i; 104 while (huffTree[j].parent != -1) //从叶子往上找到根节点 105 { 106 k = huffTree[j].parent; 107 if (j == huffTree[k].lchild) //如果是根的左孩子,则记为0 108 { 109 s = s + "0"; 110 } 111 else 112 { 113 s = s + "1"; 114 } 115 j = huffTree[j].parent; 116 } 117 cout << "字符 " << huffTree[i].ch << " 的编码:"; 118 for (int l = s.size() - 1; l >= 0; l--) 119 { 120 cout << s[l]; 121 huffTree[i].code += s[l]; //保存编码 122 } 123 cout << endl; 124 } 125 } 126 127 string Huff_Decode(Node huffTree[], int n,string s) 128 { 129 cout << "解码后为:"; 130 string temp = "",str="";//保存解码后的字符串 131 for (int i = 0; i < s.size(); i++) 132 { 133 temp = temp + s[i]; 134 for (int j = 0; j < n; j++) 135 { 136 if (temp == huffTree[j].code) 137 { 138 str=str+ huffTree[j].ch; 139 temp = ""; 140 break; 141 } 142 else if (i == s.size()-1&&j==n-1&&temp!="")//全部遍历后没有 143 { 144 str= "解码错误!"; 145 } 146 } 147 } 148 return str; 149 } 150 151 int main() 152 { 153 //编码过程 154 const int n=5; 155 Node huffTree[2 * n]; 156 string str[] = { "A", "B", "C", "D", "E"}; 157 int w[] = { 30, 30, 5, 20, 15 }; 158 Huff_Tree(huffTree, w, str, n); 159 Huff_Code(huffTree, n); 160 //解码过程 161 string s; 162 cout << "输入编码:"; 163 cin >> s; 164 cout << Huff_Decode(huffTree, n, s)<< endl;; 165 system("pause"); 166 return 0; 167 }
标签:img 解码 pre using 赫夫曼编码 size 计算 tar 有序
原文地址:https://www.cnblogs.com/TianLiang-2000/p/12839970.html