【LeetCode-动态规划】最大正方形

标签：can   etc   ret   san   暴力   http   false   最大值   else   

题目描述

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。
示例：

输入: 
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

题目链接： https://leetcode-cn.com/problems/maximal-square/

思路1

暴力法。遍历二维数组，如果当前位置是 1，就把当前位置作为正方形的左上角，先计算横向边长最长是多少，假设这个长度为 len，然后以当前位置为左上角，[1, len]范围为边长，搜索小正方形内是否全为1，记录面积最大值。代码如下：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty()) return 0;

        int rows = matrix.size();
        int cols = matrix[0].size();
        if(cols==0) return 0;

        int ans = 0;
        for(int i=0; i<rows; i++){
            for(int j=0; j<cols; j++){
                if(matrix[i][j]==‘1‘){
                    int k = j+1;
                    while(k<cols && matrix[i][k]==‘1‘) k++;
                    int len = k-j;  // 当前位置边长可能的最大值
                    bool isCandi = true;    // 如果isCandi为true，说明当前的小正方形内全为1
                    for(int x=1; x<=len; x++){
                        if(i+x>rows) break;
                        else{
                            for(int r=i; r<i+x; r++){
                                for(int c=j; c<j+x; c++){
                                    if(matrix[r][c]!=‘1‘) isCandi = false;
                                }
                            }
                            if(isCandi) ans = max(x*x, ans);
                        }
                    }
                }
            }
        }
        return ans;
    }
};

• 时间复杂度：O(m*n*min(m,n)^2)
  m，n 分别是矩阵的行列数。
• 空间复杂度：O(1)

思路2

使用动态规划。

• 状态定义：dp[i][j] 表示以位置 (i,j) 为右下角的全为 1 的正方形边长；
• 状态转移方程：dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1，也就是当前位置符合条件的边长等于当前位置左边一个位置、左上角一个位置、上面一个位置符合条件边长的最小值加 1；
• 边界条件：当只有一行或者一列时，如果 matrix[i][j] = 1, dp[i][j]=1；否则 dp[i][j]=0.

关于状态转移方程，可以参考这篇题解的解释，如下图

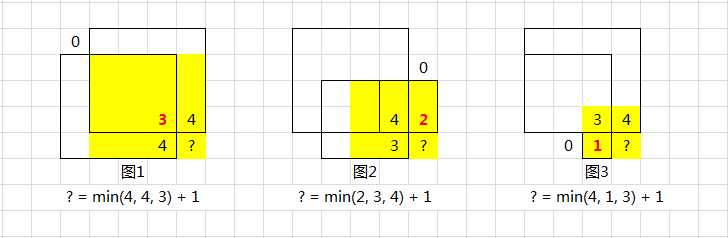
类似于木桶效应，当前位置的边长与相邻的三个位置的最小值有关。
代码如下：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty() || matrix[0].empty()) return 0;

        int rows = matrix.size();
        int cols = matrix[0].size();
        vector<vector<int>> dp(rows, vector<int>(cols, 0));
        int maxLen = 0; // 符合条件正方形的最大边长
        for(int i=0; i<rows; i++){
            for(int j=0; j<cols; j++){
                if(matrix[i][j]==‘1‘){
                    if(i==0 || j==0) dp[i][j] = 1;  // 边界条件
                    else{
                        dp[i][j] = min(min(dp[i-1][j], dp[i-1][j-1]), dp[i][j-1]) + 1;
                    }
                    maxLen = max(dp[i][j], maxLen);
                }
            }
        }
        return maxLen*maxLen;
    }
};

• 时间复杂度：O(m*n)
  m，n 分别是矩阵的行列数。
• 空间复杂度：O(m*n)

【LeetCode-动态规划】最大正方形

标签：can   etc   ret   san   暴力   http   false   最大值   else   

原文地址：https://www.cnblogs.com/flix/p/12851781.html