标签:long 红色 技术 影响 form 分享 穷举 转移 minimum
给你一个目标数组 target 和一个整数 n。每次迭代,需要从 list = {1,2,3..., n} 中依序读取一个数字。
请使用下述操作来构建目标数组 target :
题目数据保证目标数组严格递增,并且只包含 1 到 n 之间的数字。
请返回构建目标数组所用的操作序列。
题目数据保证答案是唯一的。
示例 1
输入:target = [1,3], n = 3
输出:["Push","Push","Pop","Push"]
解释:
读取 1 并自动推入数组 -> [1]
读取 2 并自动推入数组,然后删除它 -> [1]
读取 3 并自动推入数组 -> [1,3]
示例 2:
输入:target = [1,2,3], n = 3
输出:["Push","Push","Push"]
示例 3:
输入:target = [1,2], n = 4
输出:["Push","Push"]
解释:只需要读取前 2 个数字就可以停止。
提示:
1 <= target.length <= 1001 <= target[i] <= 1001 <= n <= 100target 是严格递增的class Solution {
public:
//正常判断是否需要在target数组中存储,同时如果足够了即可break
vector<string> buildArray(vector<int>& target, int n) {
vector<string>v;
int len = target.size();
int j = 0;
for(int i = 1;i <=n ;++i){
if(j == len)break;
if(i == target[j]){
v.push_back("Push");
++j;
}
else{
v.push_back("Push");
v.push_back("Pop");
}
}
return v;
}
};
给你一个整数数组 arr 。
现需要从数组中取三个下标 i、j 和 k ,其中 (0 <= i < j <= k < arr.length) 。
a 和 b 定义如下:
注意:^ 表示 按位异或 操作。
请返回能够令 a == b 成立的三元组$ (i, j , k)$ 的数目。
示例 1:
输入:arr = [2,3,1,6,7]
输出:4
解释:满足题意的三元组分别是 (0,1,2), (0,2,2), (2,3,4) 以及 (2,4,4)
示例2:
输入:arr = [1,1,1,1,1]
输出:10
示例 3:
输入:arr = [2,3]
输出:0
思路:
arr[i]...arr[j-1]的异或结果可以转化为(arr[0]...arr[j-1])(arr[0]...^arr[i-1]),因为相同的值异或为0,而异或一个0是不影响原结果的。因此事先计算出会用到的异或结果,用数组dp保存。
class Solution {
public:
int countTriplets(vector<int>& a) {
int n = a.size();
vector<int> s(n+1);
for (int i = 1; i <= n; ++ i)
s[i] = s[i-1]^a[i-1];
int ret = 0;
for (int i = 1; i <= n; ++ i)
for (int j = i+1; j <= n; ++ j)
for (int k = j; k <= n; ++ k)
{
if ((s[j-1]^s[i-1]) == (s[k]^s[j-1])) ret ++;
}
return ret;
}
};
给你一棵有?n?个节点的无向树,节点编号为?0?到?n-1?,它们中有一些节点有苹果。通过树上的一条边,需要花费 1 秒钟。你从?节点 0?出发,请你返回最少需要多少秒,可以收集到所有苹果,并回到节点 0 。
无向树的边由?edges?给出,其中?edges[i] = [fromi, toi]?,表示有一条边连接?from?和?toi 。除此以外,还有一个布尔数组?hasApple ,其中?hasApple[i] = true?代表节点?i?有一个苹果,否则,节点?i?没有苹果。
示例 1:
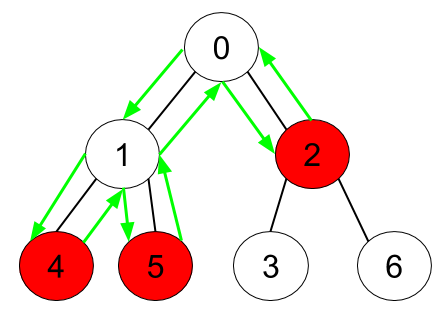
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
输出:8
解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
示例 2:
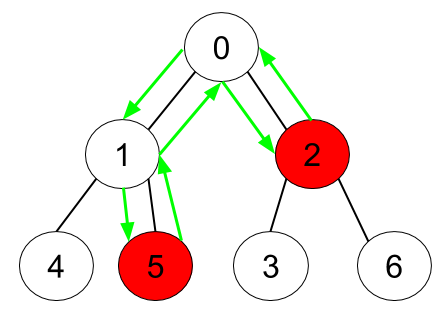
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
输出:6
解释:上图展示了给定的树,其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。
思路:
只要那个节点是true,向上一直将父节点同化,那么路径就等于:每两个连接(子、父都为true)的点的那条线x 2 后的和
class Solution {
public:
int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
int i,res=0;
//若子节点为true,则父节点同化为true
for(i=edges.size()-1; i>=0; i--)
if(hasApple[edges[i][1]]==true)
hasApple[edges[i][0]]=true;
// 收集苹果的路径即为所有节点为true的拓扑图的所有连线*2
for(i=0; i<edges.size(); i++)
if(hasApple[edges[i][1]]==true) res +=2;
return res;
}
};
给你一个 rows x cols 大小的矩形披萨和一个整数 k ,矩形包含两种字符: ‘A‘ (表示苹果)和 ‘.‘ (表示空白格子)。你需要切披萨 k-1 次,得到 k 块披萨并送给别人。
切披萨的每一刀,先要选择是向垂直还是水平方向切,再在矩形的边界上选一个切的位置,将披萨一分为二。如果垂直地切披萨,那么需要把左边的部分送给一个人,如果水平地切,那么需要把上面的部分送给一个人。在切完最后一刀后,需要把剩下来的一块送给最后一个人。
请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字,请你返回它对 10^9 + 7 取余的结果。
示例 1:
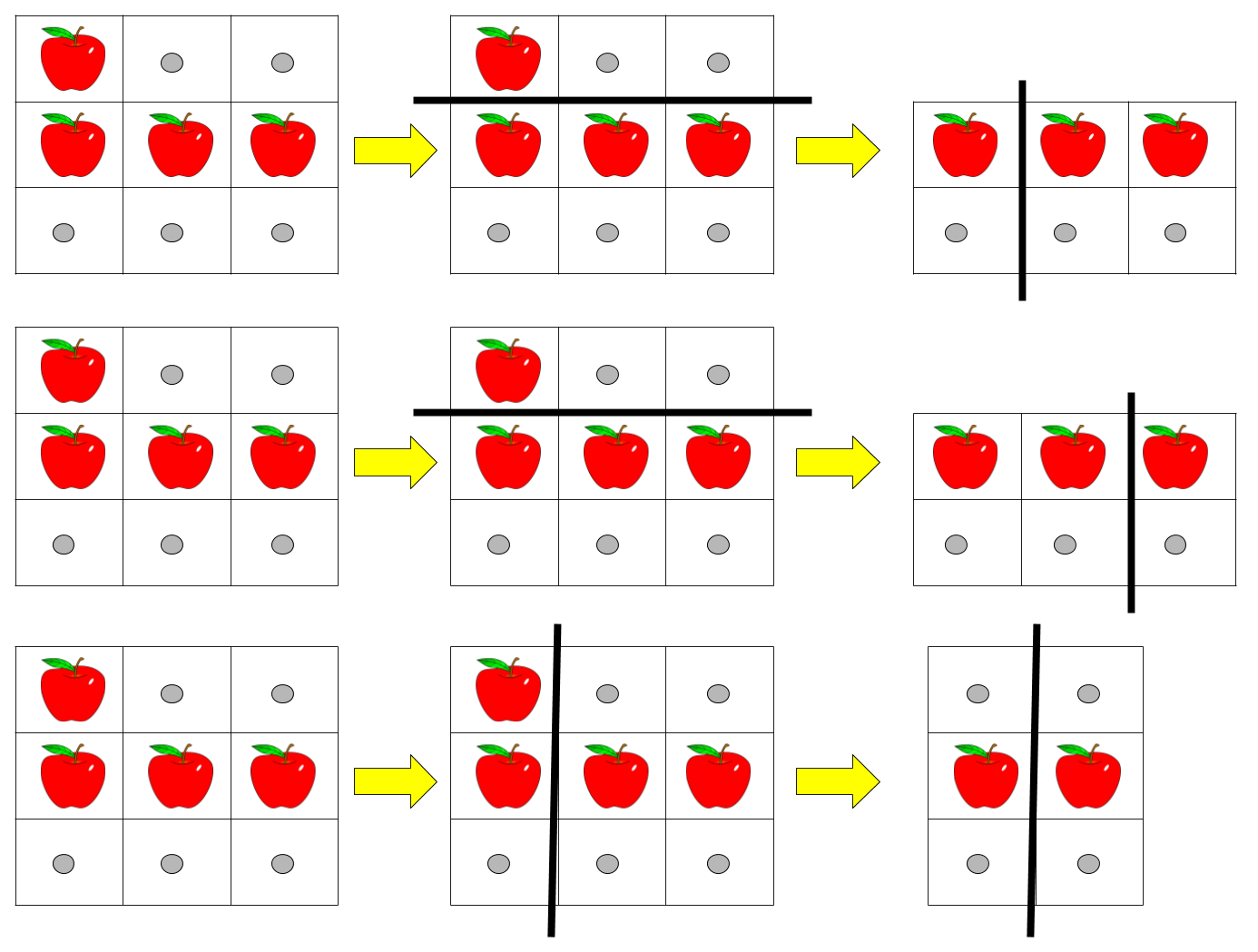
输入:pizza = ["A..","AAA","..."], k = 3
输出:3
解释:上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。
示例 2:
输入:pizza = ["A..","AA.","..."], k = 3
输出:1
示例 3:
输入:pizza = ["A..","A..","..."], k = 1
输出:1
思路:
本题是统计切割方案数,一看就是使用dp,怎么来思考呢?
首先我们考虑存在的状态数:
毫无疑问,披萨被切成k块肯定是状态之一。
而如何表示当前剩余部分的披萨呢?题中说把左边和上边给一个人,可以知道,右下部分总是会剩余下来。
所以可以记录左上角的位置来表示剩余的披萨。
因此一个三维数组可以做为dp数组:dp[i][j][k]
i,j表示披萨剩余部分的左上角,k表示当前披萨被切成k块
初始状态显而易见,由于只有一块,没有切,左上角为(0,0),所以dp[0][0][1]=1
状态转移
知道初始状态后,我们就要开始进行状态转移了~
首先让我们来考虑怎么从一块变成两块
披萨:
A..
AAA
...
由于我们知道可以水平切和垂直切,左上角为(i,j),一刀切下去,可以从k变成k+1
因此,我们可以穷举每个状态水平切和垂直切的所有切法,来得到k+1的状态。
因为每切一次得到的剩余披萨左上角都不同,所以不会出现重复。
首先水平切:
左上角为(0,0),k=1
A.. A..
+++ AAA
AAA +++
... ...
剩余部分:左上角为(1,0),k=2 剩余部分:左上角为(2,0),k=2 (不合理)
有这两种切法,很清楚看出来,第二种切法是不可以的,因为下面那一部分不存在A,不符合题意。
如何判断剩余和切出来的披萨存不存在A,我们先记下这个问题,后面会提到。
所以可以得到水平切的状态转移方程:
记原来的左上角为(i,j),新的左上角为(x,y)
if(两部分都存在A){
dp[x][y][k+1]+=dp[i][j][k]
}
垂直切是和水平切一样的,就不说了。
解决存在A的问题
我们如何判断切开后的两块披萨是否存在A呢?
方法1:直接暴力求解,我不知道会不会超时,我没有试,有兴趣可以写一下。
方法2:利用数学知识,计算出来对应披萨块中A的数量,假如数量大于0,则存在A
方法3:别的方法,假如有人愿意分享更简单的,可以在评论分享,大家一起进步
我使用方法2,所以就写一下方法2:
用数组num[i][j]表示以(0,0)为左上角,(i,j)为右下角的披萨块中包含的A数量
上例中:
num:
1 1 1
2 3 4
2 3 4
怎么计算num数组使用简单的dp和数学知识就可以了,这里就不再赘述。
通过num数组和获得披萨块的左上角和右下角就可以轻易地算出A的个数:
这个大家肯定都会,就举个例子吧,就是简单的数学关系:
例:计算以(1,0)为左上角,(2,2)为右下角的披萨块A数目:
num[2][2]-num[0][2]-num[2][-1]+num[0][-1];
下标中出现-1的num值都用0代替:所以为4-1-0-0=3
看不懂的可以直接看代码如何计算A数目,一看就明白了
#define ll long long int
class Solution {
public:
const ll mod=1e9+7;
int ways(vector<string>& pizza, int k) {
int row=pizza.size(),col=pizza[0].length();
//计算num
vector<vector<int>> num(row,vector<int>(col,0));
if(pizza[0][0]==‘A‘) num[0][0]=1;
for(int i=1;i<row;i++) num[i][0]=num[i-1][0]+(pizza[i][0]==‘A‘);
for(int i=1;i<col;i++) num[0][i]=num[0][i-1]+(pizza[0][i]==‘A‘);
for(int i=1;i<row;i++) for(int j=1;j<col;j++)
num[i][j]=num[i-1][j]+num[i][j-1]-num[i-1][j-1]+(pizza[i][j]==‘A‘);
//初始化dp
vector<vector<vector<ll>>> dp(row,vector<vector<ll>>(col,vector<ll>(k+1,0)));
dp[0][0][1]=1;
//从k=2开始填充
for(int x=2;x<=k;x++){
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
//dp为0代表不存在这种情况
if(dp[i][j][x-1]==0)
continue;
//穷举水平切
for(int z=i+1;z<row;z++){
if(hasA(num,i,j,z-1,col-1) && hasA(num,z,j,row-1,col-1)){
dp[z][j][x]+=dp[i][j][x-1];
dp[z][j][x]%=mod;
}
}
//穷举垂直切
for(int z=j+1;z<col;z++){
if(hasA(num,i,j,row-1,z-1) && hasA(num,i,z,row-1,col-1)){
dp[i][z][x]+=dp[i][j][x-1];
dp[i][z][x]%=mod;
}
}
}
}
}
//计算答案
ll ans=0;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
ans+=dp[i][j][k];
}
ans%=mod;
}
return ans;
}
//计算存在A吗
bool hasA(vector<vector<int>>& num,int sr,int sc,int er,int ec){
int num1=0,num2=0,num3=0,res;
if(sr!=0 && sc!=0) num1=num[sr-1][sc-1];
if(sr!=0) num2=num[sr-1][ec];
if(sc!=0) num3=num[er][sc-1];
return num[er][ec]-num2-num3+num1>0;
}
};
标签:long 红色 技术 影响 form 分享 穷举 转移 minimum
原文地址:https://www.cnblogs.com/RioTian/p/12863004.html