标签:color 提高 查找 font 二分法 数据表 efi 分块 family
静态查找
数据集合稳定,不需要添加,删除元素的查找
对于静态查找:可以用线性表结构组织数据,这样便可使用顺序查找算法,如果再对关键字进行排序,则可使用折半查找法或斐波那契查找法等来提高效率
动态查找
数据集合在查找的过程中需要同时添加或删除元素的查找
对于动态查找:可考虑使用二叉排序树的查找技术,另外还可使用散列表结构来解决一些查找问题
顺序查找:
从第一个(或最后一个)记录开始,逐个进行记录的关键字和给定值进行比较
1 //顺序查找,a为要查找的数组;n为数组长度,key为查找的关键字 2 int Sq_Search(int *a,int n,int key){ 3 int i; 4 for(i=0;i<=n;i++){ 5 if(a[i]==key){ 6 return i; 7 } 8 } 9 return 0; 10 }
由于每次循环都要判断两次,所以可以考虑添加一个“哨兵”来承担监视越界的问题省去一次判断,这样效率就可提高一倍;
//顺序查找,a为要查找的数组;n为数组长度,key为查找的关键字 int Sq_Search(int *a,int n,int key){ int i=n-1; a[0]=key; while(a[i]!=key) i--; return i; }
折半查找法
二分法搜索:确定待查找范围,缩小范围【O(Log?n)】
差值查找法
原理:按照数据分布的数据差值比例,按这个比例来决定下一次查找位(关键是差值要按比例分布)
按比例查找:与折半查找法相似(只不过将二分改为了按比例查而已)
例如:再字典中查找apple不会用折半查找法,而是差值查找法
1 int bin_search(int a[],int n,int key){ 2 int low=0,high=n-1,mid; 3 while(low<=high){ 4 printf("循环\n"); 5 //中心思路是:key下标/查找范围≈key/范围边缘两值的差;根据这种思想,不断缩短范围直到查找到key 6 mid=low+(key-a[low])/(a[high]-a[low])*(high-low); 7 if(a[mid]==key) 8 return mid; 9 else if(a[mid]<key)//说明key在mid的右边 10 low=mid+1; 11 else//说明key在mid左边 12 high=mid-1; 13 } 14 return -1; 15 }
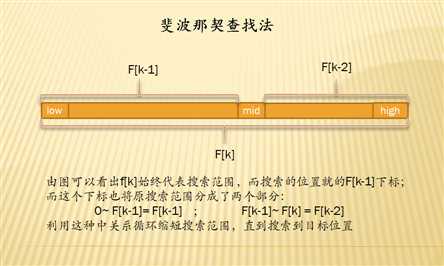
斐波那契查找
斐波那契数列(F[k]):1,1,2,3,5,8,13,21,34,...(前后两个数比重逐渐接近:0.618)
所以利用斐波那契把差值查找中的比例改为不断接近0.618的比例就叫斐波那契查找法;
1 #define MAXSIZE 20 2 3 int bin_search(int a[],int n,int key){ 4 int low=0,high,mid; 5 int i=1,j=1,k=2; 6 int f[MAXSIZE]={1,1}; 7 while(f[k]<n&&j<MAXSIZE){ 8 k++; 9 f[k]=f[i]+f[j]; 10 i=f[j]; 11 j=f[k]; 12 } 13 high=f[k]; 14 while(low<=high){ 15 printf("循环\n"); 16 mid=f[k-1]; 17 if(a[mid]==key) 18 return mid; 19 else if(a[mid]<key){//说明key在mid的右边 20 low=mid+1; 21 k-=2; 22 mid=f[k-1]; 23 }else{//说明key在mid左边 24 high=mid-1; 25 k-=1; 26 mid=f[k-1]; 27 } 28 } 29 return -1; 30 }
线性索引查找
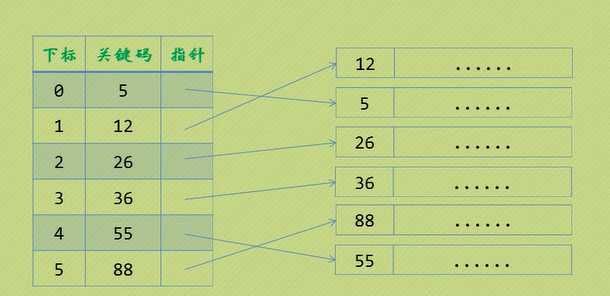 .
.
分块索引
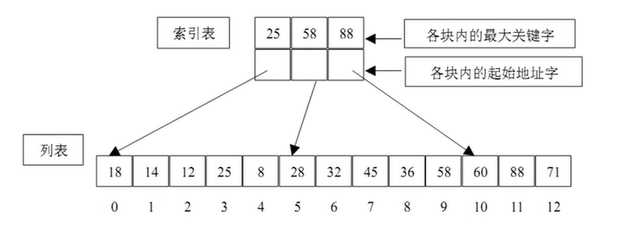
倒排索引
根据属性值来查看记录;
标签:color 提高 查找 font 二分法 数据表 efi 分块 family
原文地址:https://www.cnblogs.com/TianLiang-2000/p/12868944.html