标签:spl 一个 csdn %s com pair 多少 for 快速幂
??给定两个字符串 \(S, T\),将 \(T\) 的最后一个字符删去后,问 \(S == T\) ?
??遍历一遍。
#include <bits/stdc++.h>
using namespace std;
int main(){
string s, t; cin >> s >> t;
int len = s.size();
int mark = 0;
for(int i = 0; i < len; i ++)
if(s[i] != t[i]) {
mark = 1;
break;
}
if(mark) puts("No");
else puts("Yes");
return 0;
}
??给出 \(a, b, c, k\),意为有 \(a\) 个 \(1\),\(b\) 个 \(0\),\(c\) 个 \(-1\),你可以选 \(k\) 个数,问和最大可以是多少?
??按贪心的思路,我们选择的顺序为 \(1, 0, -1\) 。
#include <bits/stdc++.h>
using namespace std;
int main(){
string s, t; cin >> s >> t;
int len = s.size();
int mark = 0;
for(int i = 0; i < len; i ++)
if(s[i] != t[i]) {
mark = 1;
break;
}
if(mark) puts("No");
else puts("Yes");
return 0;
}
??给定如下输入:
???\(N, M, X\)
???\(C_1\ A_{1,1}\ A_{1,2}\ ...\ A_{1,M}\)
???\(C_2\ A_{2,1}\ A_{2,2}\ ...\ A_{2,M}\)
???\(...\)
???\(C_N\ A_{N,1}\ A_{N,2}\ ...\ A_{N,M}\)
??选择任意几行使得每列上的 \(A_{i,j}\) 的和 \(\geq X\),花费的代价是 \(C_i\) 的和,问最小代价可以是多少?
??直接枚举我们选择了那些行。
#include <bits/stdc++.h>
using namespace std;
const int N = 15;
int a[N][N];
int c[N];
int main(){
// 读入
int n, m, x;
cin >> n >> m >> x;
for(int i = 1; i <= n; i ++){
cin >> c[i];
for(int j = 1; j <= m; j ++)
cin >> a[i][j];
}
int ans = 1e9;
// 暴力枚举
for(int i = 0; i < 1 << n; i ++){
int b[N]; // 记录当前选择下 a 数组每列上的和
memset(b, 0, sizeof b);
int tmp = 0; // 当前选择下花费的代价
for(int j = 1; j <= n; j ++){
if((i >> (j - 1)) & 1){ // 对应位为 1 代表选了
tmp += c[j];
for(int k = 1; k <= m; k ++)
b[k] += a[j][k];
}
}
int mark = 1;
for(int j = 1; j <= m; j ++) // 判断是否满足条件
if(b[j] < x){
mark = 0;
break;
}
if(mark) ans = min(ans, tmp);
}
if(ans == 1e9) puts("-1");
else cout << ans << endl;
return 0;
}
??给定一个长度为 \(n\) 的数组 \(a\),\(i\) 可以跳跃到 \(a_i(a_i \leq n)\),那么固定你从 \(1\) 开始跳跃,问跳跃了 \(k\) 次后,你到达了那个点?
??先从 \(1\) 开始一直跳跃,直到循环,找出循环节,就可以很容易算出结果。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
typedef long long ll;
int n;
int nxt[N];
ll k;
int main(){
cin >> n >> k;
for(int i = 1; i <= n; i ++)
scanf("%d", &nxt[i]);
map<int, int> m; // 记录是否到达过
int pos = 1; // 跳跃的点
m[pos] = 1; // 初始化 1 号点
int cnt = 0; // 跳跃的次数
int ans = -1;
while(1){
pos = nxt[pos]; // 跳跃到下一个点
cnt ++; // 次数 ++
// 次数用光了,退出
if(cnt == k) { ans = pos; break; }
// m[pos] = 1,说明 pos 在之前已经到达过了,此时进入了循环
if(m[pos] == 1) break;
m[pos] = 1; // 标记
}
if(ans != -1) { cout << ans << endl; return 0; }
k -= cnt; // 减去已经跳跃的次数
int t = pos;
vector<int> node; // 记录循环节上的点
node.push_back(pos);
cnt = 0;
while(1){
t = nxt[t];
cnt ++;
node.push_back(t);
if(t == pos) break; // 循环终止
}
// 取模输出即可
cout << node[k % cnt] << endl;
return 0;
}
??有 \(N\) 个格子,和 \(M\) 种染料给格子染色,最多可以有 \(K\) 对相邻格子的颜色一样,问染色的方案数?
??考虑将一连串颜色一样的格子看作一个大格子,那么我们现在相邻大格子的颜色都不同了。假设我们现在有 \(X\) 个大格子,并且每个大格子里有 \(C_1,C_2,C_3,...,C_X\) 个小格子,那么每个大格子里都有 \(C_i - 1(1 \leq i \leq X)\) 对相邻格子的颜色一样。那么可以得到两个方程:
??显然 \(X \geq N - K\),因此我们固定了 \(X\) 的范围为 \([N - K,\ N]\)。接下来对这 \(X\) 个大格子染色,首先第一个大格子有 \(M\) 种,对于第二个大格子就只有 \(M - 1\) 了,第三个大格子也有 \(M - 1\) 种,以此类推即为 \(M \times M^{X - 1}\)。那么这 \(X\) 个大格子我们该怎么得到呢?我们可以考虑用点来划分,即在 \(N - 1\) 格(最后一个格子不能选)之间选 \(X - 1\) 个点,如图:
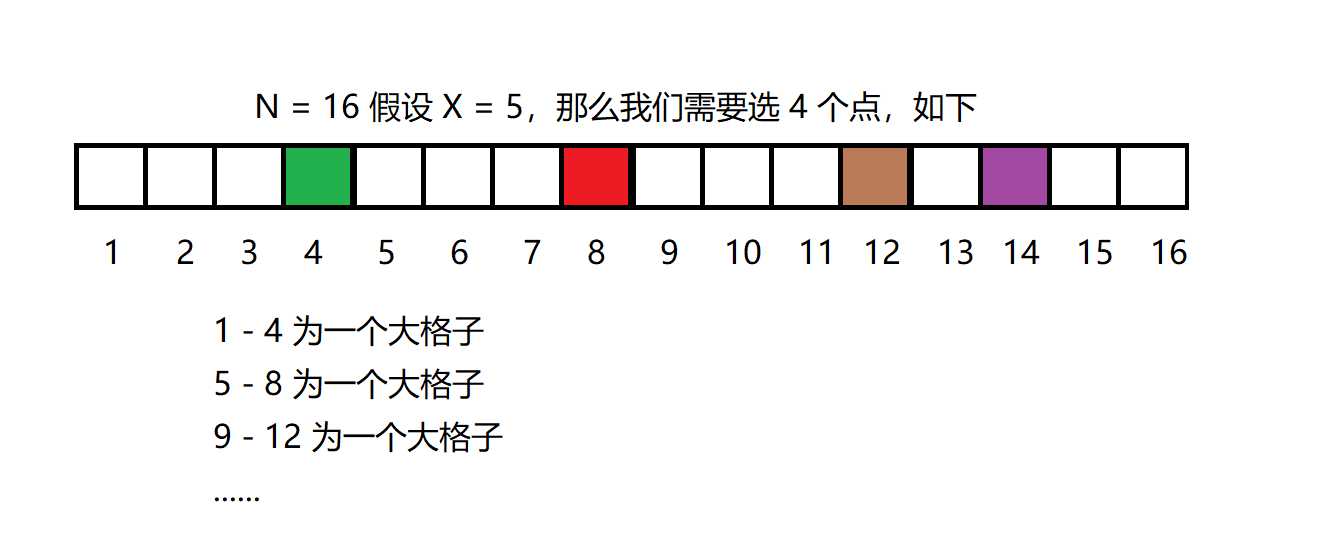
??在 \(N - 1\) 里选 \(X - 1\) 个,有 \(C_{N-1}^{X-1}\) 种,那么对于一个 \(X\) 有 \(C_{N-1}^{X-1} \times M \times M^{X-1}\) 种,在取和即:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, mod = 998244353;
typedef long long ll;
ll f[N]; // 阶乘
ll fp(ll a, ll b){ // 快速幂
ll res = 1;
while(b){
if(b & 1) res = res * a % mod;
b >>= 1;
a = a * a % mod;
}
return res;
}
ll C(ll a, ll b){ // 利用逆元计算组合数
return f[a] * fp(f[b], mod - 2) % mod * fp(f[a - b], mod - 2) % mod;
}
int main(){
ll n, m, k; cin >> n >> m >> k;
f[0] = 1;
for(int i = 1; i <= n; i ++) f[i] = f[i - 1] * i % mod;
ll ans = 0;
for(int i = n - k; i <= n; i ++){
ll tmp = C(n - 1, i - 1) * m % mod * fp(m - 1, i - 1) % mod;
ans = (ans + tmp) % mod;
}
cout << ans << endl;
return 0;
}
??给定 \(N\) 个括号序列,问是否存在一种顺序使得 \(N\) 个序列组合起来是一个合法的括号序列。
??对于一个序列,我们可以剔除掉那些已经匹配完整的括号,剩下的就是例如:\()))((,\ ))),\ (((\)这几种了,记录下多余的左括号数 \(l\),右括号数 \(r\)。那么很显然的一个事实是尽量把左括号多的放在左边,右括号多的放在右边,那么我们可以得出一种贪心的策略,即 \(l \geq r\) 的,我们把他放在左边,\(l < r\) 我们把他放在右边。那么现在分为了两大类,但具体的顺序该怎么做呢?
??对于左边的来说:我们应该按 \(r\) 从小到大来排序。
????理由:显然我们必须把 \(r = 0\) 的放在最左边,并记录当前左括号的数量为 \(t\) ,那么接下来我们放上去的字符串如果 \(r > t\) ,显然是不合法的,所以我们应该把最小的放在前面,以此类推。
??对于右边的来说:我们应该按 \(l\) 从大到小来排序。
????理由:之前已经说过,越多的左括号在左边是更优的做法。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
typedef pair<int, int> PII;
vector<PII> le, ri; // 左右两个容器
char s[N];
int main(){
int n;
cin >> n;
for(int i = 1; i <= n; i ++){
scanf("%s", s + 1);
int len = strlen(s + 1);
int l = 0, r = 0; // 左括号的数量和右括号的数量
for(int j = 1; j <= len; j ++){
if(s[j] == ‘(‘) l ++; // 遇到左括号加 +1
else{
// 如果存在左括号,就与之匹配形成一个完整的括号,所以左括号的数量 -1
if(l > 0) l --;
else r ++;
}
}
// 左括号多放在左边,注意把 r 放在前面
if(l >= r) le.push_back({r, l});
else ri.push_back({l, r});
}
sort(le.begin(), le.end()); // r 从小到大
sort(ri.begin(), ri.end(), greater<PII>()); // l 从大到小
int cnt = 0, mark = 1; // cnt 是目前剩余的左括号的数量
for(int i = 0; i < le.size(); i ++){
cnt -= le[i].first; // 减去要匹配的右括号
if(cnt < 0) { mark = 0; break; } // cnt < 0 不合法,说明左边存在右括号没有办法匹配
cnt += le[i].second;
}
for(int i = 0; i < ri.size(); i ++){
cnt -= ri[i].second;
if(cnt < 0) { mark = 0; break; }
cnt += ri[i].first;
}
if(cnt) mark = 0; // 如果最后还存在多余左括号,显然不合法
if(mark) puts("Yes");
else puts("No");
return 0;
}
AtCoder Contest 167 A - F 解题报告
标签:spl 一个 csdn %s com pair 多少 for 快速幂
原文地址:https://www.cnblogs.com/nonameless/p/12878154.html