标签:treap 排名 lse efi 子节点 span 开始 += 树的定义
本篇随笔详细讲解一下一种随机化数据结构——树堆(\(Treap\))。
首先给一个字符串等式:
所以\(Treap\)树堆其实就是树+堆。树是二叉查找树\(BST\),堆是二叉堆,大根堆小根堆都可以。
关于\(BST\)的相关知识,请看官走这边:
树堆既是一棵二叉查找树,也是一个二叉堆。但是这两种数据结构貌似还是矛盾的存在,如果是二叉查找树,就不能是一个堆,如果是一个堆,那么必然不是二叉查找树。
所以树堆用了一个很巧妙的方式解决这个问题:给每个键值一个随机附加的优先级,让键值满足二叉查找树的结构,让优先级满足二叉堆的结构。
就像下面这个样子:(图片摘自腾讯云)
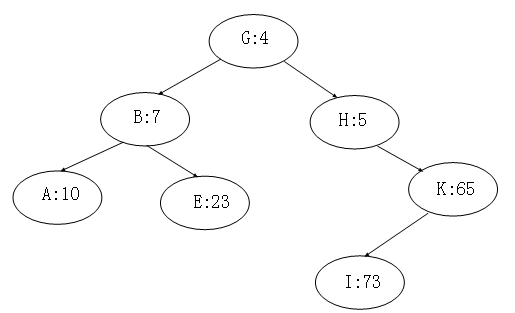
其中大写字母是键值,满足\(BST\)结构。数是优先级,满足小根堆结构。
我们在\(BST\)中讲过,普通的\(BST\)具有很强的不确定性,如果数据特殊,建树的时候可能直接变成一条链。不仅如此,插入删除的时候也很麻烦。因为如果插入或者删除,整个树原来的结构就会被打乱,这会为遍历和查找带来灾难性的后果。
所以我们推出了平衡树。就是通过将树旋转来动态维护这个树形态是平衡的,这样查找的复杂度就是\(O(log)\)级别的,是一种稳定的复杂度。
树堆是一种平衡树,它通过为键值(也就是我们需要维护成\(BST\)的)赋予优先级,使之也满足堆结构来进行旋转,成为一棵平衡树。
但是我们需要注意一点:树堆的优先级是随机赋予的。也就是说,这个数据结构其实是一个随机化的数据结构。这不是树堆的缺点,因为只有随机化赋予优先级,才有可能保证树堆的复杂度是\(O(log)\)的级别。
那么,上述性质也说明了,树堆并不是一个规则形态的二叉树,更不是堆需要满足的完全二叉树。甚至它也不符合平衡树的定义:每个节点左右子树高度相差\(\le1\),所以我们说树堆是近似实现平衡。
但是通过形态定义二叉树的方式并不绝对。我们换一种方式来对平衡树进行定义:
能够保证时间复杂度的\(BST\),就是平衡树。
首先当我们理解\(Treap\)的操作的时候,需要先对旋转这个事情有一个大体的定义。
上图:
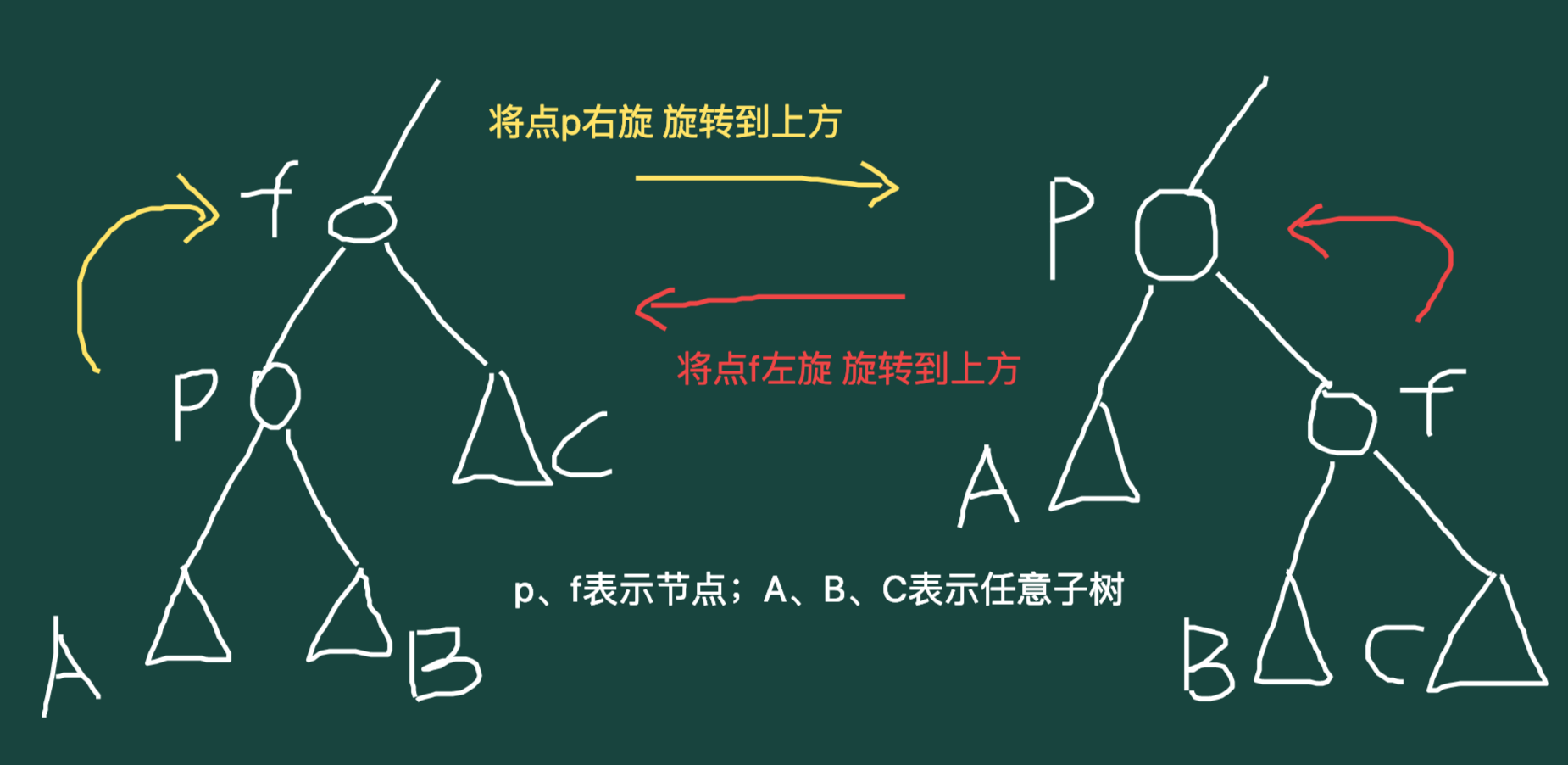
光看这个箭头的话,还是很容易理解什么是旋转的。但是可能给读者造成困扰的是:这个B节点的父亲怎么变了?
原因是这样的:我们在进行旋转操作的时候,要保证\(BST\)的节点遍历顺序是一样的,而\(BST\)的节点遍历顺序是中序遍历(这个是按\(BST\)的定义来的),也就是说只有这样才能保证遍历序不变的情况下调换节点位置。
所以,针对这个图,我们把“P/F”看成一对节点,就能很好地理解这个“左/右旋”的操作了。
首先我们了解一下\(BST\)的插入方式。其实很简单,就是一个新节点插进去,从根节点开始不停地与当前节点比大小,一直到这个节点成为叶子节点为止。
因为\(Treap\)要同时维护\(BST\)和堆,所以我们还需要在里面加上旋转操作。
如果是右儿子的话要左旋,左儿子要右旋(旋转操作请结合上图理解)。
然后我们又多统计了一个size的数据,这个数据表示子树大小,在统计当前数x是第几大的时候会很方便。
应该很简单。
struct node
{
int val,pri,size,lson,rson;//val键值,pri优先级,size子树大小。
}tree[maxn];
int tot;
void L_rotate(int &pos)
{
node x=tree[tree[pos].rson];//x表示要转到上面的节点
tree[pos].rson=x.lson;
x.lson=pos;
x.size=tree[pos].size;
maintain(pos);
tree[pos]=x;
}
void R_rotate(int &pos)
{
node x=tree[tree[pos].lson];
tree[pos].lson=x.rson;
x.size=tree[pos].size;
maintain(pos);
tree[pos]=x;
}
void maintain(int pos)
{
tree[pos].size=tree[tree[pos].lson].size+tree[tree[pos].rson].size+1;
}
void insert(int &pos,int x)
{
if(!pos)
{
pos=++tot;
tree[pos].val=x;
tree[pos].pri=rand();
}
if(x<tree[pos].val)
{
insert(tree[pos].lson,x);
if(tree[pos].pri<tree[lson].pri)//如果优先级不匹配,就旋转(这里维护的是大根堆)
R_rotate(pos);
}
else
{
insert(tree[pos].rson,x);
if(tree[pos].pri<tree[rson].pri)
L_rotate(pos);
}
maintain(pos);
}
删除操作的大体思路和插入是一样的。也是要保证删除前后满足\(Treap\)的双重结构。
大致是这样的思路:首先找到这个点在哪。然后,如果这个点已经是叶子节点,就直接将其删除,如果不是,就一层层地将它转到底部,然后进行删除。这和我们的插入操作有异曲同工之妙,就是进行操作的一定是叶子节点,如果不是叶子的话是不能粗暴删除的。需要转。
void remove(int &pos,int x)
{
if(!pos)
return;
if(x==tree[pos].val)
{
if(tree[pos].lson|tree[pos].rson)//如果非叶子节点
{
if(tree[tree[pos].lson].pri>tree[tree[pos].rson].pri)
R_rotate(pos),remove(tree[pos].lson,x);
else
L_rotate(pos),remove(tree[pos].rson,x);
maintain(pos);
}
else
pos=0;
}
else
{
if(x<tree[pos].val)
remove(tree[pos].lson,x);
else
remove(tree[pos].rson,x);
}
if(pos)
maintain(pos);
}
查询操作不涉及修改,根据树堆的双重性质,其操作是跟\(BST\)是一样的。
int rank(int pos,int x)
{
if(!pos)
return 1;
if(x<tree[pos].val)
return rank(tree[pos].lson,x);
else
return rank(tree[pos].rson,x)+tree[tree[pos].lson].size+1;
}
int rank(int pos,int x,int &cnt)
{
if(!pos)
return -1;
if(x==tree[pos].val)
return cnt+=tree[tree[pos].lson].size;
else
{
if(x<tree[pos].val)
rank(tree[pos].lson,x,cnt);
else
cnt+=(tree[tree[pos].lson].size+1),rank(tree[pos].rson,x,cnt);
}
}
int kth(int pos,int k)
{
if(!pos || k<=0 || k>tree[pos].size)
return -1;
if(k==tree[tree[pos].lson].size+1)
return tree[pos].val;
else if(k<=tree[tree[pos].lson].size)
return kth(tree[pos].lson,k);
else
return kth(tree[pos].rson,k-tree[tree[pos].lson].size-1);
}
#define INF 1e9
int prev(int pos,int x)
{
if(!pos)
return -INF;
if(x<tree[pos].val)
return prev(tree[pos].lson,x);
else
return max(tree[pos].val,prev(tree[pos].rson,x));
}
int nxt(int pos,int x)
{
if(!pos)
return INF;
if(x>=tree[pos].val)
return nxt(tree[pos].rson,x);
else
return min(tree[pos].val,nxt(tree[pos].lson,x));
}
Treap的遍历是中序遍历,遵循先左后右的原则。
void dfs(int pos)
{
if(tree[pos].lson)
dfs(tree[pos].lson);
printf("%d ",tree[pos].val);
if(tree[pos].rson)
dfs(tree[pos].rson);
}
标签:treap 排名 lse efi 子节点 span 开始 += 树的定义
原文地址:https://www.cnblogs.com/fusiwei/p/12884254.html