线性回归的扩展---多项式回归

标签：可视化   直线   一个   enter   mode   info   ima   线性   mic   

线性模型可以拟合线性问题，这是毋庸置疑的，但实际中处理的数据往往比直线更加复杂的非线性数据。这时，依然可以尝试使用线性模型来解决这个问题。

对每个特征进行加权后作为新的特征，然后在这个扩展的数据集上训练线性模型
啥意思呢，举个例子：
假设函数为：

转换函数：

这样便得到了：

这样便愉快实现了将非线性数据转换成了线性数据，困难是永远难不倒优秀的劳苦大众的
接下来，咱们又可以愉快的玩耍了
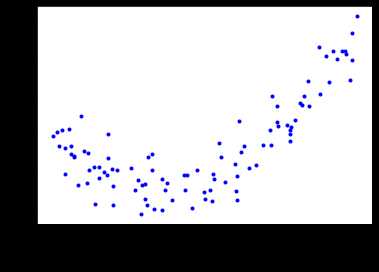
造数据(构造一个二次函数并加入噪点作为数据)

np.random.seed(42)
m = 100
X = 6* np.random.rand(m,1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m,1)

可视化显示：

数据转换：
这里我们使用Sklearn中的PolynomialFeatures类将训练数据集进行转换，让训练集中每个特征的平方作为新特征

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2,include_bias=False)
X_poly = poly_features.fit_transform(X)
print(X[0])
print(X_poly[0])

结果展示：

这是可以发现，X_poly包含了原始特征X和这个特征的平方\(X^2\)。
扩展数据集有了，现在可以使用LinearRegression模型进行拟合

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)

查看截距和系数

lin_reg.intercept_,lin_reg.coef_

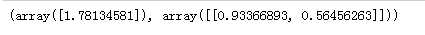
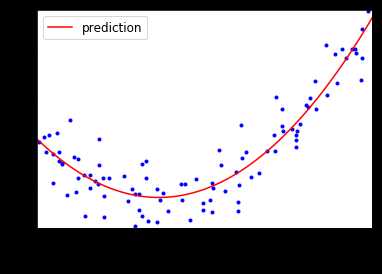
结果可视化显示

线性回归的扩展---多项式回归

标签：可视化   直线   一个   enter   mode   info   ima   线性   mic   

原文地址：https://www.cnblogs.com/whiteBear/p/12885431.html