标签:部分 状态 优先 inf 常见 大于 ret pre 算法
前言
重中之重的一个知识!也是算法设计中非常非常基础的一部分,OI 这么多年一直陪伴在身边,是大部分不能得到正解只求部分分时的最佳选择,通常我们称之为“暴力搜索”,它写起来不伤脑筋,能够处理数据量小的情况,而且有时灵机一动再优化一下,甚至能得到更可观的分数,所以其实就算对算法、理论或者数据结构不太熟悉,单单把搜索用好了,分数并不会太差。
但也因为学的很早,以至于开这一节时不禁思考一个问题——当年到底是先学的 DFS 和 BFS 还是先学的图论?理论上这两个概念是源自图论的,但是其适用范围又绝不局限于图上。
所以,我们姑且认为,这里讲述的 DFS / BFS 是广义上的搜索。
(总目录:https://www.cnblogs.com/jinkun113/p/12528423.html)
子目录列表
1、
3.1 DFS / BFS 搜索
1、DFS
DFS 英文全称为 Depth First Search,中文名为深度优先搜索,是一种用于遍历图或树的算法。其深度优先,是指在遍历过程中优先往深度更高的结点遍历,其相对概念为 BFS(广度优先搜索),会在下面介绍。
但是,DFS 更多时候并非仅仅局限于图论上的遍历——广义上的 DFS,是指用递归实现元素的遍历搜索,两者本质上是有一定差别的。一般将满足如下两种条件的过程称之为 DFS 搜索:
① 递归调用自身,直到搜索到目的地或没有可以搜索的地方
② 对访问过的元素打上访问标记,确保每个点仅访问一次
下面给出一些例子。
【例子】将 n 分解为 3 个不同的正整数,排在后面的数必须大于等于前面的数,求所有方案。比如 6 = 1 + 2 + 3。
这也太简单了?直接写上:
for (int i = 1; i <= n; i++) for (int j = i; j <= n; j++) for (int k = j; k <= n; k++) if (i + j + k == n) cout << n << ‘=‘ << i << ‘+‘ << j << ‘+‘ << k << endl;
那如果是分解为 4 个呢?四重循环?
那如果是分解为 m 个,m <= 10呢?写若干重循环显然是治标不治本的,这个时候,DFS 就有用了。
回顾一下递归(请参见:https://www.cnblogs.com/jinkun113/p/12797469.html)的思想,其整个过程是一层层地深入,直到得到最终结果。首先我们明确三大核心:
① 当前状态 dfs(int o, int d)
我们将每一重循环视作一层状态,每一层的状态都记录一些数据:当前的层数 d,当前与 n 的差值 o。
当前的层数 d,用于确定停止递归的状态,假设分解成 m 个数,则当 d = m 时说明不能再分解了,直接判断是否满足条件;
当前与 n 的差值 o,用于判断是否满足条件,如果 d = m 的同时 o = 0,说明这 m 个数之和正好为 n,为一种方案,则 ans++。
② 终止条件 d = m
在 ① 中已经提到了。
③ 下一状态 dfs(o - x, d + 1)
对于第 d 层,如果已经选择了 x 作为本层的值,则 d++, o -= x。
同时,因为题干要求数列单调递增,同时为了最后的输出,需要开一个 a 数组来记录每一层的值。
综上,核心代码为:
1 void dfs(int o, int d) { 2 if (d > m) { 3 if (!o) { 4 cout << n << ‘=‘; 5 for (int i = 1; i < m; i++) 6 cout << a[i] << ‘+‘; 7 cout << a[m] << endl; 8 } 9 return; 10 } 11 for (int i = a[d - 1] + 1; i <= o; i++) 12 a[d] = i, dfs(o - i, d + 1); 13 }
原网站的代码似乎漏洞百出,先判断 n == 0 再判断 i < m 问题很大,其次也应该写 i <= m。

注意到,前面说 DFS 的条件之一是有访问标记,这道题其实并不需要,因为在每一层枚举数的过程中并不会出现访问到曾经访问过的状态。
看到这里发现,DFS 中的 DF —— 深度优先,似乎没体现出来是什么意思。理论上,广义的 DFS 其实并不存在深度优先这个概念
再来看一道题目。
【例子】给出一个 n * m 的 0 - 1 矩阵,如图 a,小明以其中一个 1 为起点在矩阵中前进,1 能通过 0 不能通过,求问小明能走到多少个 1。

这种类型的 DFS 已经属于狭义的图论 DFS,但由于只是简单的 0 - 1 矩阵,放在这里讲也没有问题,而且能更好理解什么叫做深度优先。
橙色为小明的起点。从该位置开始为 DFS 的第一层,枚举其四个方向,判断是否能够前进——如图 b,向上向下均为 0,不能通过;向左则越界;向右为唯一路径,则进入下一层。
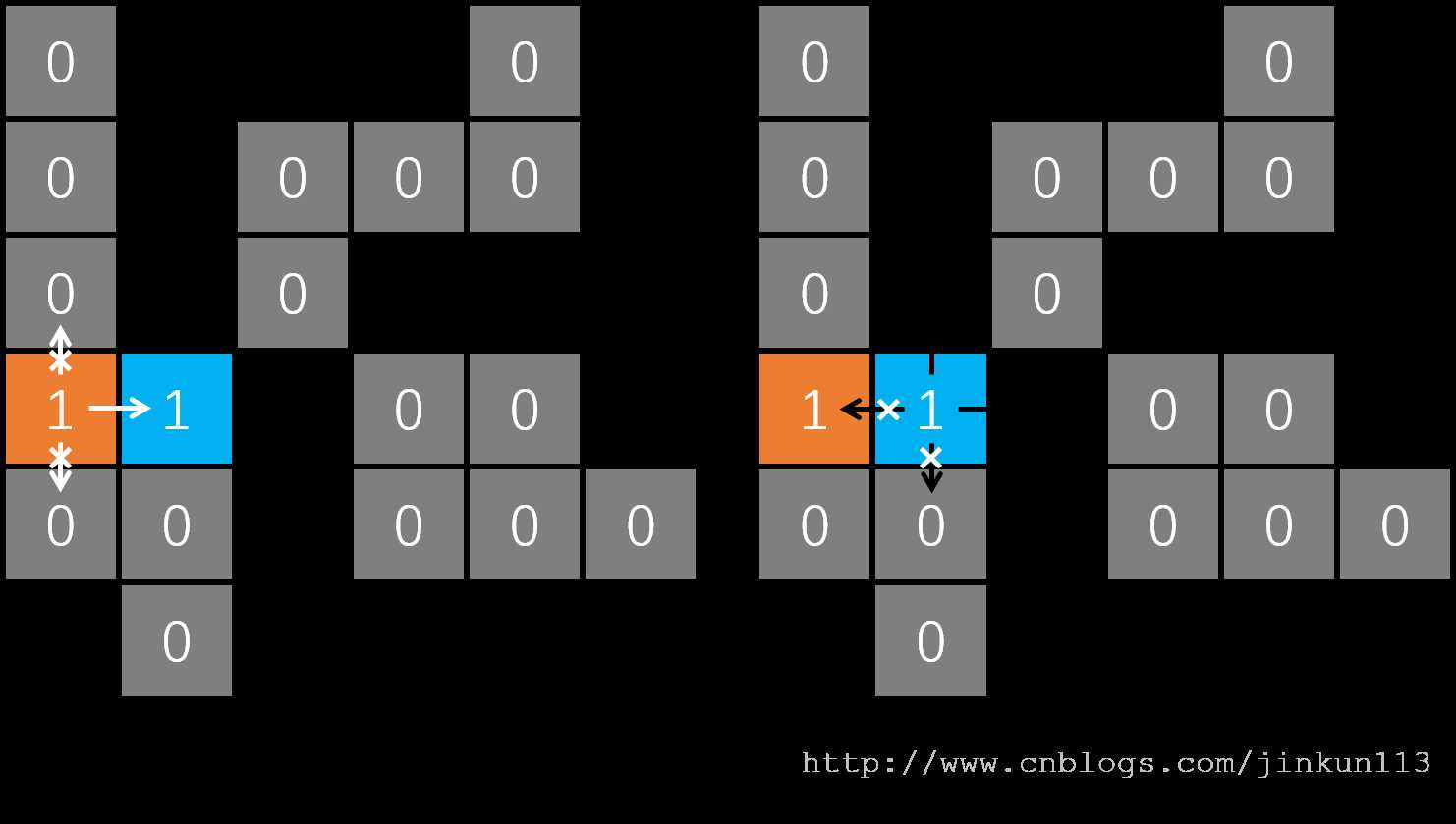
如图 c,当前位置向下为 0,不能通过;向左为 1,看起来好像可以走?然后又走到橙色的 1,然后就进入死循环了。
这个时候,访问标记的作用就体现出来了——我们建一个 vis 二维数组,对所有访问过的位置标记为 1,这样在搜索的过程中特判一下,如果该位置的 vis 值为 1,则跳过。如果没有访问标记就会进入死循环,进而栈溢出,这也是写 DFS 最为常见的问题之一。
所以接着就剩下向上和向右两个方向了,它们都可以走,至于先往哪里走,取决于代码的实现。我们假设先往上走,然后以此类推,一直走到了无路可走的地方,如图 d。对于任何一层,如果没有可走的路了,则会返回到上一层,如图 e,我们又回到了之前的位置。
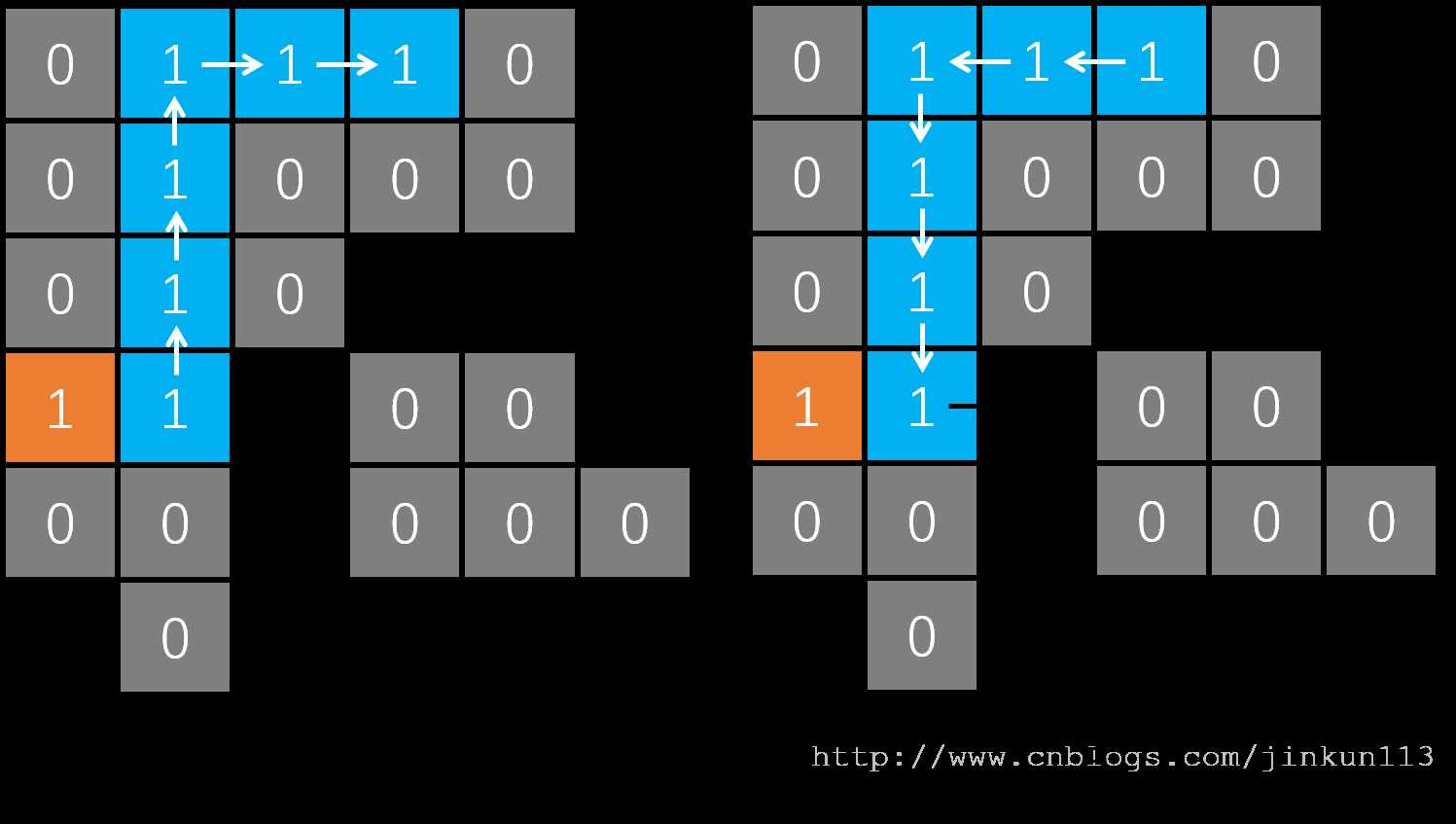
接着只剩向右走的路了,还是一样,最后走到了路的尽头,如图 f。而接下来,我们到过的所有位置都无路可走了,则一路返回到起点,如图 g,最后返回到原函数,DFS 结束。
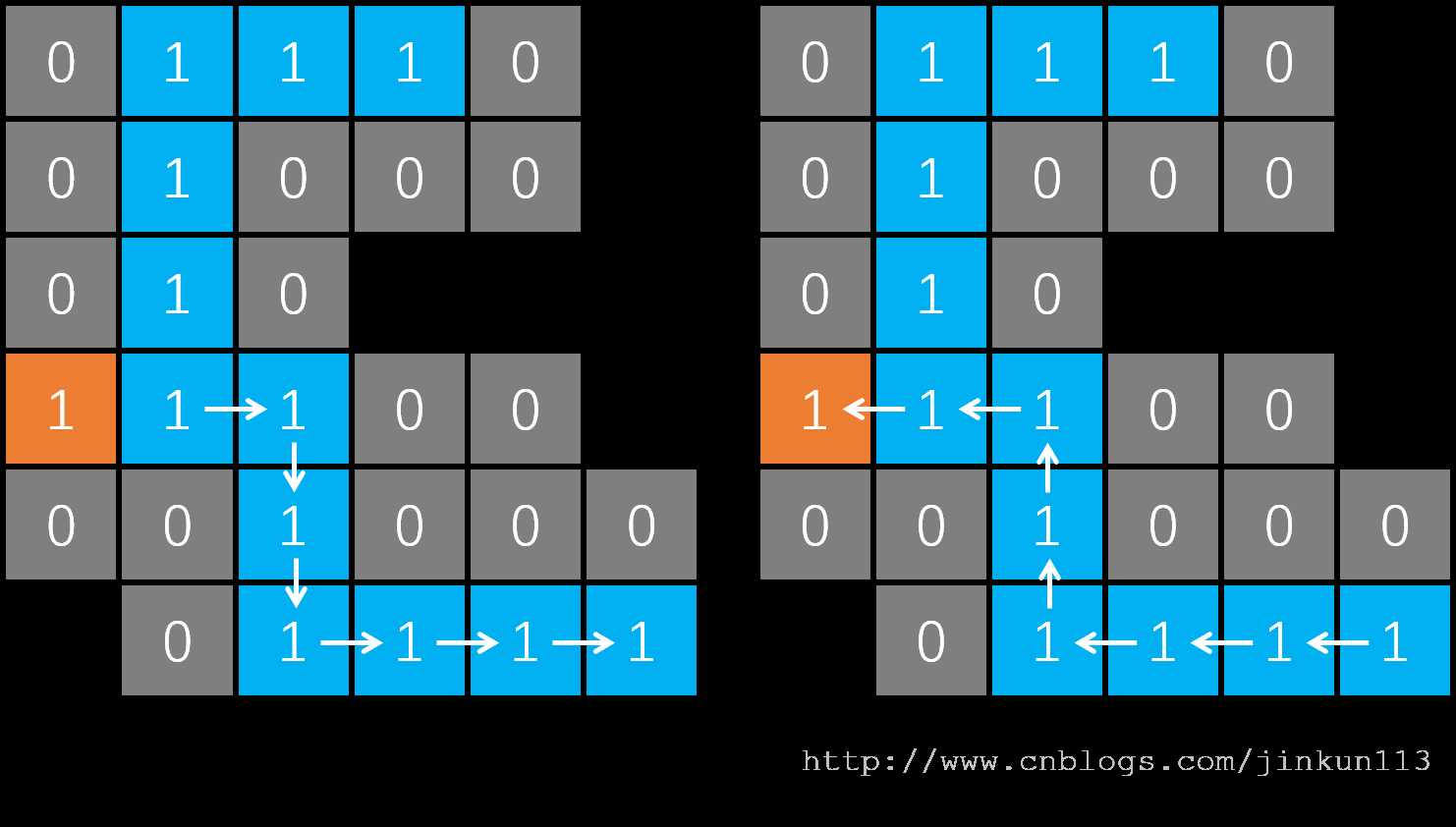
所以深度优先是什么?说白了就是一路走到底,如果发现是死胡同,则原路返回,然后在之前出现过的岔路口选择另一条路,并再次一路走到底,以此往复。
看完大致过程,还是分析下三大核心:
① 当前状态 dfs(int x, int y)
每一层只需要记录当前的位置坐标 x 和 y 即可。
② 终止条件
本题最后只需要累加 1 的个数,不存在终止条件。
③ 下一状态 dfs(x + vx, y + vy)
这也很简单,状态转移只有 4 种可能,即每个坐标的 4 个方向,vx 和 vy 均为 [0, 1]。
代码:
标签:部分 状态 优先 inf 常见 大于 ret pre 算法
原文地址:https://www.cnblogs.com/jinkun113/p/12885905.html