标签:pair ack return tor syn poj2778 需要 name 数学
传送门:http://poj.org/problem?id=2778
题目大意:基因序列仅含AGCT四个英语字母,有m个病毒,长度不超过10,现在要制造一个长度为n的基因序列,问有多少种方案,使得我的基因序列不含有病毒子串。
样例输入:
4 3
AT
AC
AG
AA
首先对于所有病毒先跑AC自动机,然后可以得到一张图,对于AC自动机建立的trie树,我们可以看做是一张图,起点在空串上,每个点加上一个新字母之后可以到达一个新的点。而这张图上,有部分点是不能经过的非法点,分别是字符串末尾和fail指针为非法点的点。
以样例为例,建出来的图是这样的:
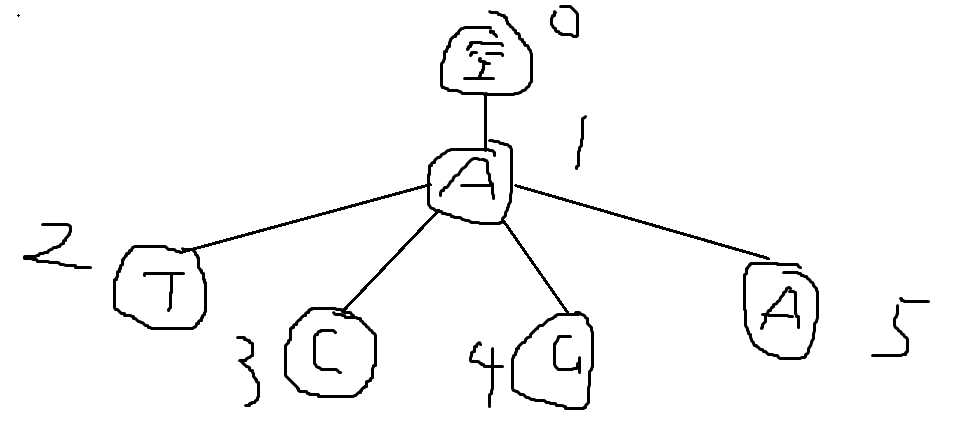
其中,2,3,4,5点位非法点,0,1为合法点。根据AC自动机上trie树的转移方案,可以得到任意两点之间的转移方案,即路径数,采用邻接矩阵表示,mat[i][j]表示i->j路径数,样例表示为:
\begin{pmatrix}
3 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 1 & 1 & 1\\
3 & 1 & 0 & 0 & 0 & 0\\
3 & 1 & 0 & 0 & 0 & 0\\
3 & 1 & 0 & 0 & 0 & 0\\
3 & 1 & 0 & 0 & 0 & 0
\end{pmatrix}
而由于部分点是不可选的非法点,因此我们将和这些点相邻的点删除,矩阵变为了
\begin{pmatrix}
3 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 9 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0
\end{pmatrix}
随后要用到离散数学的知识,对于这个矩阵的n次方,所得到的矩阵matrix,matrix[i][j]表示i->j走过n步路之后的方案数。因此,只需要求该矩阵的n次方,随后将第一行加起来即可,矩阵快速幂求解即可。最后贴上AC代码:
#include<iostream> #include<queue> #include<cstring> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; typedef pair <ll,ll> pii; #define rep(i,x,y) for(int i=x;i<y;i++) #define rept(i,x,y) for(int i=x;i<=y;i++) #define per(i,x,y) for(int i=x;i>=y;i--) #define all(x) x.begin(),x.end() #define pb push_back #define fi first #define se second #define mes(a,b) memset(a,b,sizeof a) #define mp make_pair #define dd(x) cout<<#x<<"="<<x<<" " #define de(x) cout<<#x<<"="<<x<<"\n" #define debug() cout<<"I love Miyamizu Mitsuha forever.\n" const int inf=0x3f3f3f3f; const int maxn=205; const int mod=100000; int id(char ch) { if(ch==‘A‘) return 0; if(ch==‘G‘) return 1; if(ch==‘C‘) return 2; if(ch==‘T‘) return 3; } class Trie { public: Trie() { cnt=1; } int cnt; int trie[maxn][5]; int fail[maxn]; bool bad[maxn]; void insert(string s) { int len=s.size(); int pos=0; rep(i,0,len) { int next=id(s[i]); if(!trie[pos][next]) trie[pos][next]=cnt++; pos=trie[pos][next]; } bad[pos]=1; } void getfail() { queue<int> q; rep(i,0,4) { if(trie[0][i]) { fail[trie[0][i]]=0; q.push(trie[0][i]); } } while(!q.empty()) { int pos=q.front(); q.pop(); bad[pos]|=bad[fail[pos]]; rep(i,0,4) { if(trie[pos][i]) { fail[trie[pos][i]]=trie[fail[pos]][i]; q.push(trie[pos][i]); } else { trie[pos][i]=trie[fail[pos]][i]; } } } rept(i,0,cnt) { rep(j,0,4) if(!trie[i][j]) { trie[i][j]=trie[fail[i]][j]; } } } }t; class matrix { public: ll arrcy[105][105]; int row,column; matrix() { memset(arrcy,0,sizeof arrcy); column=row=0; } friend matrix operator *(matrix s1,matrix s2) { int i,j; matrix s3; for (i=0;i<s1.row;i++) { for (j=0;j<s2.column;j++) { for (int k=0;k<s1.column;k++) { s3.arrcy[i][j]+=s1.arrcy[i][k]*s2.arrcy[k][j]; s3.arrcy[i][j]%=mod; } } } s3.row=s1.row; s3.column=s2.column; return s3; } void show() { for(int i=0;i<row;i++) { for (int j=0;j<column;j++) cout<<arrcy[i][j]<<" "; cout<<endl; } } }mat; matrix quick_pow(matrix s1,long long n) { matrix mul=s1,ans; ans.row=ans.column=s1.row; memset(ans.arrcy,0,sizeof ans.arrcy); for(int i=0;i<ans.row;i++) ans.arrcy[i][i]=1; while(n) { if(n&1) ans=ans*mul; mul=mul*mul; n>>=1; } return ans; } string s; int main() { ios::sync_with_stdio(false); cin.tie(0); int n,len; cin>>n>>len; rep(i,0,n) { cin>>s; t.insert(s); } t.getfail(); mat.row=mat.column=t.cnt; rept(i,0,t.cnt) { if(t.bad[i]) continue; rep(j,0,4) { if(!t.bad[t.trie[i][j]]) mat.arrcy[i][t.trie[i][j]]++; } } // mat.show(); mat=quick_pow(mat,len); int ans=0; rept(i,0,t.cnt) ans=(ans+mat.arrcy[0][i])%mod; cout<<ans<<"\n"; return 0; }
poj2778 DNA Sequence(AC自动机+矩阵快速幂)
标签:pair ack return tor syn poj2778 需要 name 数学
原文地址:https://www.cnblogs.com/FZUzyz/p/12885877.html