标签:-- 还需 lol 贪心 get name 城市 简单 调整
对于这种题目,我们可以先算出以 \(u\) 为头的毛毛虫,然后再算趴在节点 \(u\) 上的毛毛虫。题解
由于题目的设定我们可以发现,一个子树一旦进去就必须走完这个子树的所有点才能出来,所以肯定设计 \(dp\) 状态 \(f_u\) 代表这棵子树从进入到全部安装好需要多少时间。
然后我们发现,如果这样没法转移,因为安装的时候你并不用呆在子树中。呆在子树中的时间应该是运送所需要的时间,即子树边权的和的两倍。于是我们记这个为 \(g_u\)。
到上面都是基础的简单操作。现在我们要看决策,即安排先安装哪个子树的。
进入一个子树后,我们肯定先安装根节点的,因为这不耗费任何时间(原树不是,因为题目规定根节点一定是最晚装的)。然后对于子树,我们采取一个贪心。显然贪心大概就是按照 \(f_v-g_c\) 从大到小排序。用调整发乱搞一番就可以知道贪心是对的。
于是搞个优先队列维护即可。
int a[N],f[N],g[N];
struct node {
int g,fg;
bool operator < (const node&b) const{return fg<b.fg;}
bool operator > (const node&b) const{return fg>b.fg;}
};
void dp(int u,int fa) {
priority_queue<node>q;
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa) {
dp(v,u); g[u]+=(g[v]+2);
q.push((node){g[v]+1,f[v]-g[v]});
}
int sumg=0;
while(!q.empty()){
int gv=q.top().g,fgv=q.top().fg; q.pop();
sumg+=gv, f[u]=max(f[u],sumg+fgv); sumg++;
}
if(u!=1) f[u]=max(f[u],a[u]);
else f[u]=max(f[u],sumg+a[u]);
}
int main() {
int n; scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1,u,v,w;i<n;i++)
scanf("%d%d",&u,&v),add(u,v),add(v,u);
dp(1,0);
printf("%d",f[1]);
return 0;
}
我们对 \(k\) 进行二分答案。
对于一个节点 \(u\),如果 B 走到了 \(u\),那么在下一步前必须保证 \(u\) 的所有儿子节点都被染色。完成染色有两种方法:第一种,在下一步前赶快把这几个点全部染上;第二种,在 B 走到 \(u\) 前就染上这里的一些点。当然,如果可以选择第一种,那么就没有必要选择第二种,我们总是希望可以独立完成任务然后造福后人。
所以我们可以设立状态,表示这个节点需要自己的祖先提前染色多少节点才能覆盖住整个子树。题解
首先肯定进行二分答案。
对于一个 \(mid\),我们需要选择不多于 \(m\) 个节点使得 关键节点到这几个点的最小距离 比 mid 小,也就是说,让这 \(m\) 个节点到这些点的每个最小距离每个都不大于 \(mid\)。那么可以这样看,即选择 \(m\) 个点,用距离为 \(mid\) 的圆覆盖这个子树。所以我们需要记录一下这个点到最远的未被覆盖关键节点的距离 \(f\)。
由于我们希望能减少选择的节点(不能超过 \(m\)),所以我们需要选择一个最靠近上面的节点去覆盖这个子树的一些点和上边的部分。记录 \(u\) 子树中选择点离 \(u\) 的距离最近为 \(g_u\)。
转移方程也比较清晰。\(f_u=\max{f_v+1}\),\(g_u=\min {g_v}+1\)。
但是对于一些情况需要特判。
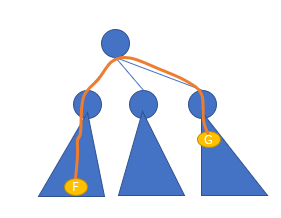
如果 \(u\) 本身就是关键节点,而且 \(g>mid\),那么这个点就没法被覆盖了,只能让父亲节点去处理自己。所以 \(f_u=\max(0,f_u)\),这个 \(0\) 代表自己无法被处理。
如果橙色路径(\(f+g\))不比 \(mid\) 大,意味着整个子树都能背覆盖,那么 \(f\) 就应该等于 \(-\infty\)。
如果 \(f_u=mid\),那么自己就必须成为选择点,否则那个最远的关键节点将终身无人覆盖。所以 \(g_u=0,f_u=-\infty\)
int n,m,im[N],k,f[N],g[N],cnt;
inline int read(){
int x=0,f=1; char ch=getchar();
while(ch<‘0‘||ch>‘9‘) {if(ch==‘-‘) f=-1;ch=getchar();}
while(ch>=‘0‘&&ch<=‘9‘) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
inline void dp(register int u,int fa){
f[u]=-inf,g[u]=inf;
for(register int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
dp(v,u);
f[u]=max(f[u],f[v]+1);
g[u]=min(g[u],g[v]+1);
}
if(im[u]&&g[u]>k) f[u]=max(f[u],0);
if(f[u]+g[u]<=k) f[u]=-inf;
if(f[u]==k) g[u]=0,f[u]=-inf,cnt++;
}
int main(){
n=read(),m=read();
if(n==3e5) return puts("79244"),0;
for(int i=1;i<=n;i++) im[i]=read();
for(int i=1,u,v;i<n;i++)
u=read(),v=read(),add(u,v),add(v,u);
int l=0,r=n,ans=0;
while(l<=r){
k=(l+r)>>1;
cnt=0; dp(1,0);
if(f[1]>=0) cnt++;
if(cnt<=m) ans=k,r=k-1;
else l=k+1;
}
printf("%d",ans);
return 0;
}
树形背包的转移为 \(f_{u,i+j}=\operatorname{combine}(f_{u,i},f_{v,j})\)。其中,在处理每个子节点的时候,需要用 \(g\) 数组备份 \(f\) 并初始化 \(f\)。然后后面转移中需要用到的截止到上一个子节点的 \(f\) 用 \(g\) 替代即可。
转换一下,我们可以转换成求在服务 \(x\) 个用户时的最大盈利。然后进行朴素转移。
int n,m,a[N];
int sz[N],f[N][N],g[N],ans;
void dfs(int u){
for(int i=1;i<=m;i++) f[u][i]=-1e9;
if(!e[u].size()) sz[u]=1,f[u][1]=a[u];
for(int p=0;p<e[u].size();p++){
int v=e[u][p]; dfs(v);
for(int i=0;i<=m;i++) g[i]=f[u][i],f[u][i]=-1e9;
for(int i=0;i<=min(sz[u],m);i++)
for(int j=0;j<=min(sz[v],m-i);j++){
f[u][i+j]=max(f[u][i+j],g[i]+(j!=0)*(f[v][j]-w[u][p]));
}
sz[u]+=sz[v];
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1,k,v,ww;i<=n-m;i++){
scanf("%d",&k);
for(int j=1;j<=k;j++)
scanf("%d%d",&v,&ww),e[i].push_back(v),w[i].push_back(ww);
}
for(int i=1;i<=m;i++) scanf("%d",&a[n-m+i]);
dfs(1);
for(int i=0;i<=m;i++) if(f[1][i]>=0) ans=i;
printf("%d",ans);
return 0;
}
树形背包好题,用到了很多技巧,比如 int 转 longlong (尽管卡空间是很屑的行为)然后转移方程很长。
\(f(u,x,0/1,0/1)\) 表示点 \(u\) 子树,用 \(k\) 个监听器,\(u\) 装/未装监听器,\(u\) 有/没有被覆盖。题解
先做一遍普通的以原点的为根的树形 \(dp\),然后再做一次 \(dfs\),将自己的儿子换上来然后颠倒父子关系(即更新所求答案),得出自己作为根时的计算。
从更直观的理解,也可以记录自己子树的信息+外部世界的信息从而得出答案。
由于可以 \(O(n^2)\),枚举每条删边。枚举删边之后对于两个树分别求出在这棵树中距离节点 \(u\) 的最远距离。
显然,我们要连接两个树的“交通枢纽”,即到其他点距离最大的长度最小的那个点。然后连接。于是这个结果就是第一棵树的直径,第二棵树的直径和重新连边后的直径的最大值。题解
同样二次扫描。第一次算出子树内贡献。然后第二次加上子树外贡献(即祖先和自己的兄弟子树)。
int a[N],f[N],sum[N],g[N],t,ans=0x3f3f3f3f3f3f3f3f;
void dfs1(int u,int fa){
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
dfs1(v,u);
sum[u]+=sum[v];
f[u]+=(f[v]+sum[v]*e[i].w);
}
sum[u]+=a[u], g[u]=f[u];
}
void dfs2(int u,int fa){
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
g[v]=g[u]+(t-sum[v]*2)*e[i].w;
dfs2(v,u);
}
ans=min(ans,g[u]);
}
signed main(){
int n; scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]), t+=a[i];
for(int i=1,u,v,w;i<n;i++)
scanf("%lld%lld%lld",&u,&v,&w),add(u,v,w),add(v,u,w);
dfs1(1,0), dfs2(1,0);
printf("%lld",ans);
return 0;
}
每一次换根,子树内节点深度减少1,子树外节点深度增加1。所以总的深度总和会增加 \(n-sz_u\),减少 \(sz_u\),所以每一次还需要记录一下子树大小。
int n,sz[N],d[N],ans,num,tmp;
inline int read(){
int x=0,f=1; char ch=getchar();
while(ch<‘0‘||ch>‘9‘) {if(ch==‘-‘) f=-1;ch=getchar();}
while(ch>=‘0‘&&ch<=‘9‘) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void dfs1(int u,int fa) {
for(register int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
d[v]=d[u]+1;
dfs1(v,u);
sz[u]+=sz[v];
}
sz[u]++, tmp+=d[u];
}
void dfs2(int u,int fa) {
if(tmp>ans) num=u,ans=tmp;
for(register int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
int ptmp=tmp, pszu=sz[u], pszv=sz[v];
tmp+=(n-2*sz[v]), sz[u]=n-sz[v], sz[v]=n;
dfs2(v,u);
tmp=ptmp, sz[u]=pszu, sz[v]=pszv;
}
}
signed main() {
n=read();
for(register int i=1,u,v;i<n;i++)
u=read(),v=read(),add(u,v),add(v,u);
dfs1(1,0);
dfs2(1,0);
printf("%lld",num);
return 0;
}
同样二次扫描,\(f(u,j)\) 代表范围为 \(j\) 及以内的权值和。先处理子树,再处理总体。注意算总体的时候要用到之前子树的东西,所以要小心计算顺序(本题即倒过来算)。
int n,k,c[N],f[N][K];
void dfs1(int u,int fa){
for(int i=0;i<=k;i++) f[u][i]=c[u];
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
dfs1(v,u);
for(int j=1;j<=k;j++) f[u][j]+=f[v][j-1];
}
}
void dfs2(int u,int fa){
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
for(int j=k;j>=2;j--) f[v][j]+=(f[u][j-1]-f[v][j-2]);
f[v][1]+=c[u];
dfs2(v,u);
}
}
signed main(){
scanf("%lld%lld",&n,&k);
for(int i=1,u,v;i<n;i++)
scanf("%lld%lld",&u,&v),add(u,v),add(v,u);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
dfs1(1,0), dfs2(1,0);
for(int i=1;i<=n;i++) printf("%lld\n",f[i][k]);
return 0;
}
题目可以转换为求出对于这个点的子树内/外,最大可以移掉的且大小不超过 \(\frac{n}{2}\) 的子树大小。这个可以用换根dp做掉。题解
这题一大难点在于读题……然后涉及一些脑洞(对于我来说)。
最终化简成:要修改点权,使得每个节点的所有子节点的点权一样,且和为这个节点的点权。
显然,一旦确定一个点的点权,所有其他点点权都可以确定,于是我们枚举每一个点(脑洞 \(1\))
第二,枚举每一个点,判断如果它不修改自己的权值,那么算出根最终的存储(因为每个不同的根的存储代表不同的情况)。最后,我们看根节点存储 \(x\) 时有多少节点不需要动(即有多少节点不动时可以达成这个根节点存储的值)。然后取 \(max\) 即可。(脑洞 \(2\))
我们计算一下,当点 \(u\) 是 \(a_u\) 时,根节点的值应该是 \(a_u\) 乘上从自己父节点到根节点的所有子结点个数的乘积。显然这个会炸 longlong。于是这里用到了很神奇的脑洞:连乘取 log 就变成了连加!即 \(\log (xy)=\log (x) + \log (y)\),最后离散化求这个 \(\max\) 即可 (脑洞 \(3\) )
int a[N],cnt[N],ans,now; double lcnt[N];
void dfs(int u,int fa){
for(int i=hd[u],v;i;i=e[i].nxt) if((v=e[i].to)!=fa) cnt[u]++;
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
lcnt[v]=lcnt[u]+log(cnt[u]*1.);
dfs(v,u);
}
lcnt[u]+=log(1.*a[u]);
}
int main(){
int n; scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1,u,v;i<n;i++)
scanf("%d%d",&u,&v),add(u,v),add(v,u);
dfs(1,0);
sort(lcnt+1,lcnt+n+1);
for(int i=1;i<=n;i++){
if(lcnt[i]-lcnt[i-1]>1e-9) ans=max(ans,now),now=0;
now++;
} ans=max(ans,now);
printf("%d",n-ans);
return 0;
}
对于 \(3\) 个点,一定是第三个点到前两个点的 LCA 的距离等于前两个点到 LCA 的距离。所以我们从 LCA 去统计这三个点的数量。
稍微进行转换,对于每个点,我们可以提取它为根节点,然后距离相等就转换为深度。然后由于我们要保证 LCA 是这个根,所以根的每个孩子的子树只能提取一个点。
不过由于如果直接统计每个子树深度为 \(d\) 有多少,是 \(O(n^3)\) 的,所以我们需要动态求解。我们要记录在子树 \(u\) 前统计的,深度为 \(d\), 选出一个节点有 \(g\) 种,选出两个节点有 \(h\) 种。
int d[N],dm,f[N],g[N],h[N],ans;
void dfs(int u,int fa){
d[u]=d[fa]+1; f[d[u]]++; dm=max(dm,d[u]);
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa)
dfs(v,u);
}
signed main(){
int n; scanf("%lld",&n);
for(int i=1,u,v;i<n;i++)
scanf("%lld%lld",&u,&v),add(u,v),add(v,u);
for(int root=1;root<=n;root++){
memset(g,0,sizeof(g)),memset(h,0,sizeof(h));
for(int i=hd[root],v;i;i=e[i].nxt){
memset(f,0,sizeof(f)); d[root]=dm=0;
dfs(v=e[i].to,root);
for(int j=1;j<=dm;j++){
ans+=h[j]*f[j];
h[j]+=g[j]*f[j];
g[j]+=f[j];
}
}
}
printf("%lld",ans);
return 0;
}
先dfs基环树找环,不过这题只要找出环上的两个点即可。要么第一个点不能选,要么第二个点不能选,所以答案就是 \(\max{f_{u,0},f_{v,0}}\)。
int n,a[N],ans; double k;
int r1,r2; bool vst[N]; bool found=0;
void dfs(int u,int fa){
vst[u]=1;
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
if(vst[v]){
r1=u,r2=v;
e[i].go=e[i^1].go=0;
found=1;
return;
}
dfs(v,u);
if(found) return;
}
}
int f[N][2];
void dp(int u,int fa){
for(int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa&&e[i].go){
dp(v,u);
f[u][0]+=max(f[v][1],f[v][0]);
f[u][1]+=f[v][0];
}
f[u][1]+=a[u];
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1,u,v;i<=n;i++)
scanf("%lld%lld",&u,&v),add(u+1,v+1),add(v+1,u+1);
scanf("%lf",&k);
dfs(1,0);
dp(r1,0); ans=f[r1][0];
memset(f,0,sizeof(f)),dp(r2,0); ans=max(ans,f[r2][0]);
printf("%.1lf",ans*k);
return 0;
}
还有一种判断环的方式 —— 并查集。如果连接的两个点已经连通,那么这条边一定是环上边。
由于每个连通块有且仅有一个环,所以我们对于每个环上边做上面讲到的 \(dp\) 即可。
#include<bits/stdc++.h>
#pragma optimize("Ofast,unroll-loop")
using namespace std;
const int N=1e6+9;
struct edge{int to,nxt;}e[N*2]; int hd[N],tot,ecnt[N];
void add(int u,int v){e[++tot]=(edge){v,hd[u]},hd[u]=tot;}
int n,a[N],id[N],r1,r2; int reu[N],rev[N],cnt;
long long f[N][2],ans;
inline int find(int i){return (id[i]==i?i:id[i]=find(id[i]));}
inline void unite(int u,int v){id[find(u)]=find(v);}
inline int read(){
register int x=0; register char c=getchar();
while(c<‘0‘||c>‘9‘) c=getchar();
while(c>=‘0‘&&c<=‘9‘){x=(x<<3)+(x<<1)+c-48,c=getchar();}
return x;
}
void dp(int u,int fa){
f[u][0]=f[u][1]=0;
for(register int i=hd[u],v;i;i=e[i].nxt)
if((v=e[i].to)!=fa){
dp(v,u);
f[u][0]+=max(f[v][0],f[v][1]);
f[u][1]+=f[v][0];
}
f[u][1]+=a[u];
}
signed main(){
n=read();
for(int i=1;i<=n;i++) id[i]=i;
for(int i=1,v;i<=n;i++){
a[i]=read(),v=read();
id[i]=find(i),id[v]=find(v);
if(id[i]!=id[v]) unite(i,v),add(i,v),add(v,i);
else reu[++cnt]=i,rev[cnt]=v;
}
for(register int i=1;i<=cnt;i++){
r1=reu[i],r2=rev[i];
long long tmp=0; dp(r1,0); tmp=f[r1][0];
dp(r2,0); tmp=max(tmp,f[r2][0]);
ans+=tmp;
}
printf("%lld",ans);
return 0;
}
标签:-- 还需 lol 贪心 get name 城市 简单 调整
原文地址:https://www.cnblogs.com/TetrisCandy/p/TreeDP.html