标签:不同 概念 分析 $$ 结束 begin 表示 定义 code
残量网络
从直观上看,给定网络$G$和流量$f$,残量网络$G_f$由那些仍有空间对流量进行调整的边构成。流网络允许的额外流量等于其容量减去该边的流量:$c_f(u, v) = c(u, v)-f(u, v)$,差值为正则将这条边置于图$G_f$中。由于只允许有额外流量的边加入图$G_f$,若$c_f(u,v)=0$的话,则该边不属于图$G_f$。
残留网络$G_f$还可能包含图$G$中不存在的边。算法对流量进行操作的目标是增加总流量,为此,算法可能对某些特定边上的流量进行缩减。为了表示对于一个正流量$f(u, v)$的缩减,我们将边$(v,u)$加入到图$G_f$中,并将其残存容量设为$c_f(v, u)=f(u, v)$。也就是说,一条边能允许的反向流量最多将其正向流量抵消。图$G_f$中的反向边允许将发送过来的流量发送回去,等同于缩减该条边的流量,也称为抵消操作。这类抵消操作对任何最大流算法都是非常关键的,在许多算法中也都是必须的。
更形式化地,考虑结点对$u, v\in V$,残量容量$c_f(u, v)$如下:
$$c_f(u, v)=\left\{\begin{matrix}
c(u,v)-f(u,v) & if\ (u,v)\in E\\
f(u,v)& if\ (v,u)\in E\\
0& Others
\end{matrix}\right.$$
下图为给定网络$G$和其残量网络$G_f$:
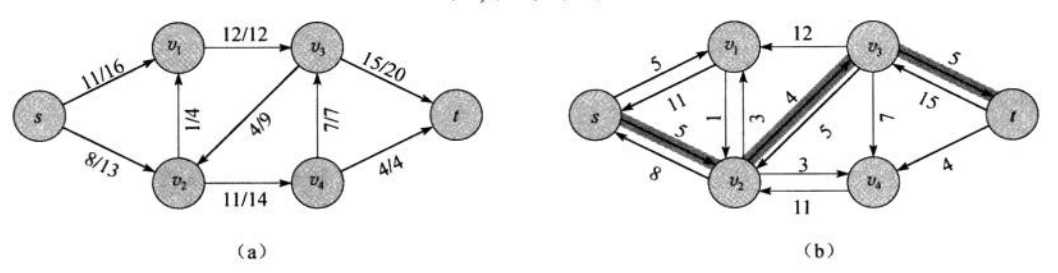
(通俗的来讲,无论对于残量网络中哪条边,都表示其还能再有多少流量经过。只不过可能含义不同。$(u, v)$的含义是增加这条边的流量,$(v, u)$的含义为减少这条边的流量,它们都能对流量进行调整)
增广路径
给定网络$G=(V, E)$和流$f$,增广路径$p$是残量网络中一条从源结点$s$到汇点$t$的简单路径。
我们在一条增广路径$p$上能够为每条边增加的流量的最大值为:
$$c_f(p) = min\left \{ c_f(u, v):\ (u, v)\in route \ p \right \}$$
流网络的切割
$Ford-Fulkerson$算法核心是沿着增广路径重复增加路径上的流量,知道找到一个最大流为止。我们怎么知道在算法终止时,确实找到一个最大流呢?而最大流最小割定理告诉我们,一个流是最大流当且仅当其残量网络不包含任何增广路径。
我们先来看一下流网络中的切割概念,做一点小分析。
网络流$G=(V, E)$中一个切割$(S, T)$将节点集合$V$划分为$S$和$T=V-S$两个集合,使得$s\in S, t\in T$。
净流量$f(S, T)$如下:$$f(S, T) = \sum_{u\in S}\sum_{v\in T}f(u, v)-\sum_{u\in S}\sum_{v\in T}f(v, u)$$
切割$(S,T)$的容量是:$$c(S,T)=\sum_{u\in S}\sum_{v\in T}c(u, v)$$
一个网络的最小切割是整个网络中容量最小的切割
如下图1-2所示,从$s$运送到$t$的物品必然通过跨越$S$和$T$的边,则有:
$$|f|=f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u, v)-\sum_{u\in S}\sum_{v\in T}f(v, u)\leqslant \sum_{u\in S}\sum_{v\in T}f(u, v)\leqslant \sum_{u\in S}\sum_{v\in T}c(u, v)=c(S,T)$$
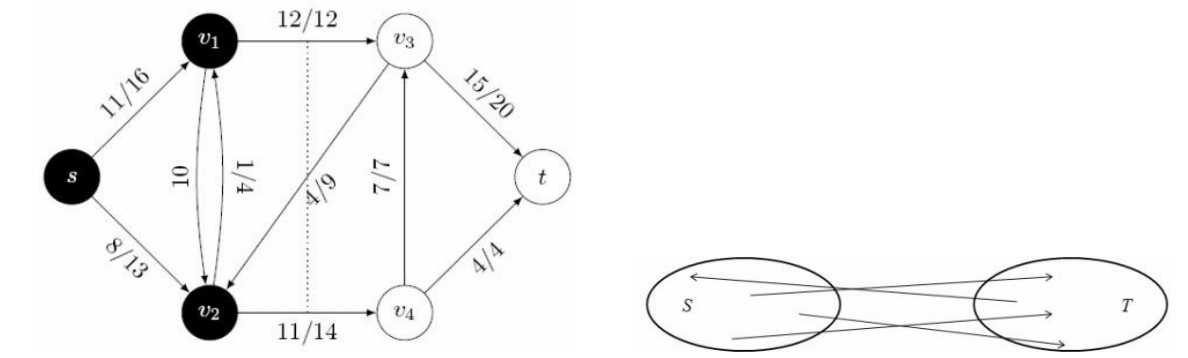
图1-1 图1-2
[最大流最小割定理] 设$f$为流网络$G=(V, E)$中的一个流,该流网络的源节点是$s$,汇点为$t$,则下列条件是等价的:
1.$f$是$G$的一个最大流。
2.残量网络$G_f$不包括任何增广路径。
3.$|f|=c(S, T)$,其中$(S, T)$是流网络$G$的某个切割
简要证明如下:
如果$G_f$不包含任何增广路径,即不存在$s$到$t$的路径。我们定义$S = \left \{ v\in V: G_f中存在s到v的路径 \right \}$,$T=V-S$。显然划分$(S,T)$是流网络$G$的一个切割。
对于一对结点$u\in S$和$v\in T$。若$(u, v)\in E$,则必有$f(u, v)=c(u, v)$;若$(v, u)\in E$,则必有$f(u, v)=0$。否则,在残量网络$G_f$中就有跨越集合$S$到到$T$的边,和不包含增广路径的条件是相悖的。
于是我们就得到了:
$$f(S, T) = \sum_{u\in S}\sum_{v\in T}f(u, v)-\sum_{u\in S}\sum_{v\in T}f(v, u)=\sum_{u\in S}\sum_{v\in T}c(u, v)-\sum_{u\in S}\sum_{v\in T}0=c(S,T)$$
又对所有切割$(S,T)$,都满足$|f|\leqslant c(S, T)$,即$|f|_{max}\leqslant c(S, T)_{min}$。稍加证明就可以得到:在增广路算法结束时,$f$是$s-t$的最大流,$(S,T)$是图的$s-t$最小割
标签:不同 概念 分析 $$ 结束 begin 表示 定义 code
原文地址:https://www.cnblogs.com/wizarderror/p/12891227.html