标签:drag ram 计算 sum 五步 png code mos tle
一、卡方分布
1. 定义
设 X1..Xn是服从标准正态分布的随机变量,则称统计量
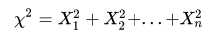
服从自由度为n的卡方分布(标准正态分布随机变量的平方和),记为,其中v称为自由度。
卡方分布期望和方差:
。
2. 外形(取决于自由度)
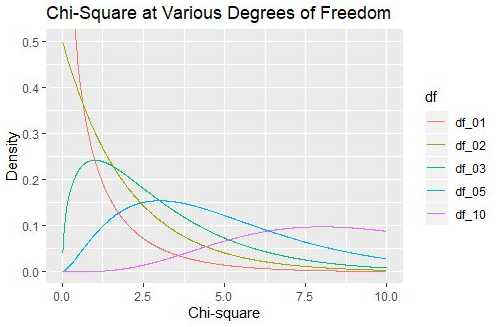
3. 统计量计算
,
为实际频数,
为期望频数。
4. 分布的两个主要用途
分布主要用于检查实际结果与期望结果之间是否存在显著差别。
二、卡方检验
1. 利用分布进行假设检验步骤
2. 自由度v
自由度值 = 独立的期望频数 - 限制条件数 = (行数-1)* (列数-1)
3. 计算拒绝域
分布进行检验为单侧检验,右侧作为拒绝域,临界值 =
(查表可得)
4. 计算统计量
5. 查看统计量是否位于拒绝域内
若统计量位于临界值内或者p值小于显著性水平,则有充分利用拒绝H0。
三、例题
1. 下表列出某骰子的观察频数,查看这些数据,并以1%的显著性水平进行检验,检验是否有足够正确说明骰子不公正。(拟合优度,检验一组数据与指定分布的吻合程度)
| 数值 | 1 | 2 | 3 | 4 | 5 | 6 |
| 频数 | 107 | 198 | 192 | 125 | 132 | 248 |
第一步:确定H0 H1
H0:骰子公正,即每面概率为1/6。
H1:骰子不公正
第二步:计算期望频数和自由度
| 数值 | 1 | 2 | 3 | 4 | 5 | 6 |
| 期望频数 | 167 | 167 | 167 | 167 | 167 | 167 |
自由度 = 6-1=5
第三步:确定拒绝域
显著性水平 = 0.01 ,自由度 = 5,则 = 15.09,于是拒绝域为>15.09的范围。
第四步:计算检验统计量
= 88.24
第五步:查看统计量是否位于拒绝域内
由于=88.24>15.09,所以统计量位于拒绝域内。
第六步:做出决策
在显著性水平为1%的情况下,有足够理由拒绝原假设。
2.我们想知道不吃晚饭对体重下降有没有影响,显著性水平=0.05(检验变量之间的相关性)
| 体重下降 | 体重未下降 | 合计 | 体重下降率 | |
| 吃晚饭组 | 123 | 467 | 590 | 20.85% |
| 不吃晚饭组 | 45 | 106 | 151 | 29.80% |
| 合计 | 168 | 573 | 741 | 22.67% |
第一步:确定H0 H1
H0:不吃晚饭对体重下降没有影响,即吃不吃晚饭的体重下降率相等;
H1:不吃晚饭对体重下降有显著影响,即吃不吃晚饭的体重下降率不相等
第二步:计算期望频数和自由度
| 体重下降 | 体重未下降 | 合计 | |
| 吃晚饭 | 133.765 | 456.234 | 590 |
| 不吃晚饭 | 34.2348 | 116.765 | 151 |
| 合计 | 168 | 573 | 741 |
自由度 = (2-1)(2-1) = 1
第三步:计算拒绝域
显著性水平=0.05 ,自由度 = 1,则 = 3.84
第四步:计算检验统计量
= 5.498
第五步:查看统计量是否位于拒绝域内
由于 = 5.498>3.84,统计量位于拒绝域内,有理由拒绝H0,认为不吃晚饭对体重下降有显著影响。
2020-05-16 15:41
标签:drag ram 计算 sum 五步 png code mos tle
原文地址:https://www.cnblogs.com/fuyusheng/p/12900701.html