标签:模拟 clu priority lin 描述 include 上进 ima 直接
马上就要开学了!!!
为了给回家的童鞋们接风洗尘,HZOI帝国的老大决定举办一场狂欢舞会。
然而HZOI帝国头顶上的HZ大帝国十分小气,并不愿意给同学们腾出太多的地方。所以留给同学们开party的地方只有一个教室。
这个教室里有一个长条形的舞池,这个舞池最多能让n个人同时在上面high,也就是说有n个位置,但要知道HZ大帝国对同学们间的接触限制很严(众所周知一群糙老爷们儿也是能够非正常接触的),所以实际上两个人是不可以在相邻的位置上high的。
由于不同的位置high起来的感觉不是很一样,所以每个位置都有一个high值。
但是有强迫症的老大对这个舞池设计不是很满意,于是他下令把条形的舞池改造成了圆环状,也就是说第1个位置和第n个位置现在相邻了。
所以,你的任务是计算合法安排好所有同学所能达到的最大high值和。
输入包括两行:
第一行有两个正整数:n,m,代表舞池有n个位置,有m个童鞋要参加狂欢
第二行有n个整数:high[i]即第i个整数代表舞池第i个位置的high值
输出共一行:
一个整数即安排好所有同学能达到的最大high值和
如果无法安排好所有的同学,则输出“High!!!”(不含引号)。
输入
5 2
1 2 3 4 5
输出
8
输入
8 3
2 7 14 8 -3 0 4 9
输出
24
1 \(\leq\) m \(\leq\) n \(\leq\) 200000
| high[i] | \(\leq\) 2000
这题的根源是这儿:https://www.luogu.com.cn/problem/P1484
当时我看到这个题就寻思着要整个环,思路基本上是不变的,也算是整了个活,然后就有了这道题。然鹅后来突然发现它下面就有一道名字一毛一样的题,对没错,就是顶着国家集训队名头的那个种树……不过那题的数据范围有点尴尬,那题的很多标程的无解是直接用n<2m判过去的,数据也的确能过,但n=m=1时实际上它是有解的。这一点我开始时就被标程给带跑了,后来还是LC大锅hack了我一波(笑)。
一开始只有一个很普通的样例可能迷惑性很强,所以到一半时我又加了一个样例2,应该是能卡掉不少代码的,也不知道有人看见了没……
题意我觉得我的语文应(shen)该(me)还(dou)可(bu)以(shi),就不给大家复述了。
好吧还是简单说一下:就是在一个有n个点的环上取m个点,使这m个点两两不相邻,且取到的权值和最大。
可能有神犇想到用DP,但是200000的数据并不是那么友好。
这题的思路其实就是贪心,但要用到一个很巧妙很巧妙的技巧
首先最简单的贪心估计大家都能想到,那就是建一个大根堆,一个个取,每取一个把两旁相连的点都标记上不能再取。
这肯定是最原始的贪心,无论什么操作都是在这个思路之上进行的。
那么,这个思路到底哪里有毛病呢?
我们简单地模拟一下:7 14 8 0 这4个数中选两个
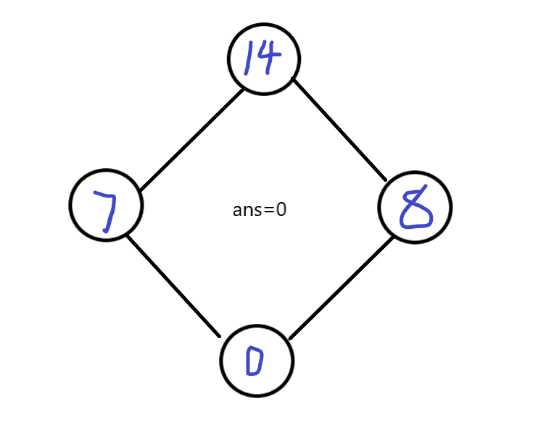
照我们刚才的思路,肯定第一步先取14,然后7跟8就标记上不能取了
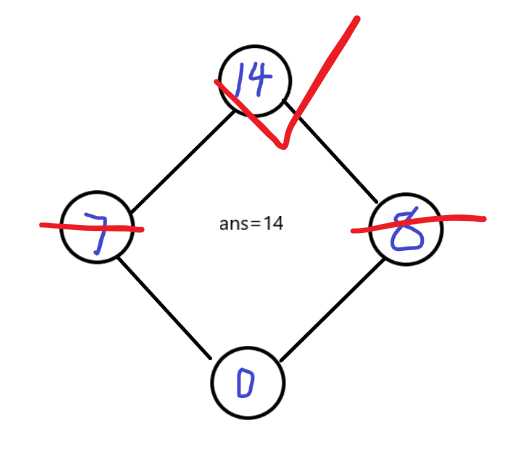
显然下一步我们能取的只有0,这样算出来最优值是14
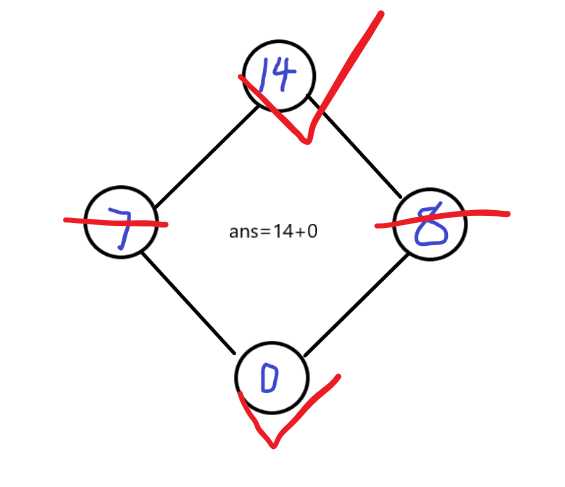
但是很显然,如果我们直接取7跟8,和是15,显然比咱们现在的14要大。
问题就出在:在点数允许的情况下,我们没有判断当前取出的这个14跟它左右相连的7跟8的和的关系,也就是说我们不能保证全局最优。
可以选择判断a[i-1].w + a[i+1].w - a[i].w与0的大小,如果大于0,我们要这两个点而不要最大的那个点。
但真正去运算时肯定不允许你这样做,我们一次这个运算只能从三个数中做一个选择,那么放到整个程序里就是从n个数中取3个数的组合数,这还是没算别的常数的说。时间显然是不允许的。
所以就要用到下面这个肥常肥常神奇的技巧:
struct node{
int w,l,r;
}a[maxn];//存储每个节点的信息
我们简单开一个结构体,w代表当前节点的权值,l为左节点编号,r为右节点编号。
还是刚才的思路,建大根堆,每次取最大权值点,标记左右两点,但不一样的地方是:我们取完这个点后,再往根堆里插一个新的点,这个新点的权值为原来左右节点的权值和-原来该节点权值,左节点为原左节点的左节点,右节点为原右节点的右节点。
这样实际上有什么用呢?回到我们出错的原因:因为我们每次只能保证在当前情况下取最大那个数是最优的,这是贪心的基础,但我们不能保证这个选择在全局上也是最优的。所以我们需要一个保险,这个新点就是为我们提供一个后悔的选项。
我们记新点的权为 a[i-1].w + a[i+1].w - a[i].w
在当前这一步,我们选择了a[i].w,因为它最大,然后插入新点。那么,如果我们能在取到这个新点之前结束运算,那么显然选择最大的这个数就是最优选择。但如果我们一直取下去直至取到了这个新点,那么说明在刚刚的那一步中a[i].w并不是最优选择,所以我们取到了这个新点,ans就相当于在之前加上了a[i].w,然后现在又加上了a[i-1].w + a[i+1].w - a[i].w
前后合起来刚好是a[i-1].w + a[i+1].w,对于整个答案来说就相当于我们刚才那步选择了左右节点,而没有选择最大节点
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring>
#include <iostream>
#define lson(x) a[x].l
#define rson(x) a[x].r
using namespace std;
const int maxn=200000+10;
int n,ans,m;
bool vis[maxn];
struct node{
int w,l,r;
}a[maxn];//存储每个节点的信息
struct Node{
int val,id;
Node();
Node(int x,int y){
val=x,id=y;
}
bool operator <(const Node x)const{
return val<x.val;
}
};
priority_queue<Node> q;//大根堆
//为了方便这里直接用左右儿子来解释,实际上是左右相连的点
void Update(int x){//删去一个节点x后更新与x相关的节点
lson(x)=a[lson(x)].l;//新点的左儿子变为原来左儿子的左儿子
rson(x)=a[rson(x)].r;//新点的右儿子变为原来右儿子的右儿子
a[lson(x)].r=x;
a[rson(x)].l=x;
}
int main(){
scanf("%d %d",&n,&m);
int maxx=-1<<15;//可不要设成-1哦,最小值有-2000呢
for(int i=1;i<=n;i++){
scanf("%d",&a[i].w);
maxx=max(a[i].w,maxx);
a[i].l=i-1;
a[i].r=i+1;
q.push(Node(a[i].w,i));
}
if(m==1){//特判掉n=m=1的情况
printf("%d\n",maxx);
return 0;
}
if(n<(m<<1)){//别的情况就可以直接n<2m判掉了
printf("High!!!\n");
return 0;
}
a[1].l=n,a[n].r=1;//所谓的环就只有这一步
for(int i=1;i<=m;i++){
while(1){
if(vis[q.top().id]) {q.pop();continue;}//标记过的点直接pop掉
break;
}
int val=q.top().val,num=q.top().id;
q.pop();
ans+=val;
vis[lson(num)]=vis[rson(num)]=1;//左右相连的点标记为访问过
a[num].w=a[lson(num)].w+a[rson(num)].w-a[num].w;//插入一个新点,新权值为原左右儿子的权值和减去原权值
Update(num);//更新新点的左右儿子信息
q.push(Node(a[num].w,num));
}
printf("%d\n",ans);
return 0;
}
标签:模拟 clu priority lin 描述 include 上进 ima 直接
原文地址:https://www.cnblogs.com/Zfio/p/12902936.html