标签：png   就会   优化   ++   图片   意思   不同的   nbsp   约数   

题意

　　给出一个n，要求求出1到n的所有数的约数个数和。

思路过程及代码

　　如果一个一个数暴力去求，那么复杂度接近n根号n。这里不把暴力的代码给出来。

　　现在我们考虑每个约数的贡献，约数x对总约数个数和的贡献为n/x，换句话说1到n含约数x的有n/x个，为什么呢？x的倍数的约数自然含x，换句话说现在就是在求n个数含多少个x的倍数，所以用n/x就行。所以我们得到了一个O(n)的算法。

ll gao(ll n){
    ll ans=0;
      for(ll i=1;i<=n;i++){
          ans+=n/i;    
    }
      return ans;
}

　　O(n)的算法看起来还不错，但我们还可以继续优化，很多地方的n/i是一样的，如果我们能一次性求出每个不同的n/i，那么就可以优化了。

　　我们来看n=10的例子

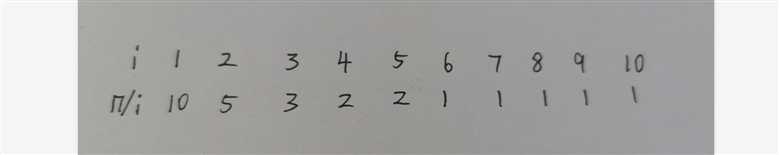
　　通过观察我们可以看到，n/i相同的列都是连续的，这是因为这里的除是整除，n/i其实就是真实值的整数部分。

　　那么如果我们能求出每一个n/i的区间长度，那么他们的贡献就是长度*(n/i)了

　　现在我们设n/i=t，n/i=t的最末位置为j，那么对应就是这一段表

　　我们只要求出j，那么长度就是j-i+1了

　　那么j怎么求呢，因为n/i=t，t是向下取整的，那么n/t的值就会对应向上增，增到j，什么意思呢？例如n=11，i=4和5的值对应的n/i都是2，11/4=2.75=2，11/5=2.2=2，那么11/2就等于5.5=5就等于j了，是不是很神奇，于是乎对于每个n/i=t的不同t，我们算一遍就行。我们可以得到一个近似O(√n)的算法

ll gao(ll n){
    ll ans=0;
      for(ll i=1,j;i<=n;i=j+1){
          j=n/(n/i);
        ans+=(j-i+1)*(n/i);    
    }
      return ans;
}

求1到n的约数个数

标签：png   就会   优化   ++   图片   意思   不同的   nbsp   约数   

原文地址：https://www.cnblogs.com/qq2210446939/p/12905431.html