视角的转化

标签：image   lin   结合   com   反思   case   mic   alpha   span   

前言

在高中数学的学习中，有好几个数学素材，需要转化视角来学习和使用。

三角求值

需要将形如\(\theta+\cfrac{\pi}{4}\)的角看成一个整体角；比如下例，

例1【2017枣庄模拟】设\(\alpha\)为锐角，\(cos(\alpha+\cfrac{\pi}{6})=\cfrac{4}{5}\)，求\(sin(2\alpha+\cfrac{\pi}{12})\)的值；

分析：注意到已知角为一个\(\alpha+\cfrac{\pi}{6}\)，未知角也是一个\(2\alpha+\cfrac{\pi}{12}\)，故二者之间的联系可能是从余、补、半、倍、特的角度建立联系，

故将已知角二倍得到\(2(\alpha+\cfrac{\pi}{6})=2\alpha+\cfrac{\pi}{3}\)，发现还是和未知角不一样，故做差就发现，\(2\alpha+\cfrac{\pi}{12}=2(\alpha+\cfrac{\pi}{6})-\cfrac{\pi}{4}\)，

故\(sin(2\alpha+\cfrac{\pi}{12})=sin[2(\alpha+\cfrac{\pi}{6})-\cfrac{\pi}{4}]=sin[2(\alpha+\cfrac{\pi}{6})]cos\cfrac{\pi}{4}-cos[2(\alpha+\cfrac{\pi}{6})]sin\cfrac{\pi}{4}\)

\(=2sin(\alpha+\cfrac{\pi}{6})cos(\alpha+\cfrac{\pi}{6})cos\cfrac{\pi}{4}-[2cos^2(\alpha+\cfrac{\pi}{6})-1]sin\cfrac{\pi}{4}=\cdots=\cfrac{17\sqrt{2}}{50}\).

• 备注：复杂一些的题目可能需要用到互余、互补、半角、倍角、特殊角中的某两个以上的角度才可以求解；

需要将形如\(\theta+\cfrac{\pi}{4}\)的角看成角\(\theta\)和角\(\cfrac{\pi}{4}\)两个角的和；比如下例，

垂直平行

例1【2016江苏高考卷】如图，在直三棱柱\(ABC-A_1B_1C_1\)中，\(D\)、\(E\)分别是\(AB\)、\(BC\)的中点，点\(F\)在侧棱\(BB_1\)上，且\(B_1D\perp A_1F\)，\(A_1C_1\perp A_1B_1\)。

求证：(1)直线\(DE//\)平面\(A_1C_1F\).

分析：现在需要\(\Leftarrow\)直线\(DE//\)平面\(A_1C_1F\)

\(\Leftarrow\)直线\(DE//\)平面\(A_1C_1F\)内的某直线\(?\)

某条直线可能是三角形的边界线，三角形中线，高线，中位线，或者需要我们做出的某条辅助直线。

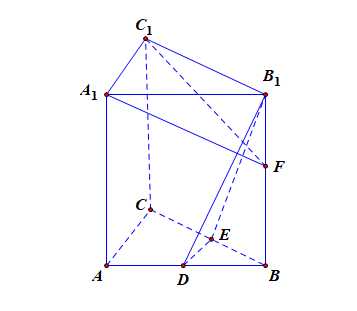
证明：因为\(D\)、\(E\)分别是\(AB\)、\(BC\)的中点，则有\(DE//AC//A_1C_1\)，

又因为直线\(A_1C_1\subsetneqq\)平面\(A_1C_1F\)，

\(DE\not\subseteq\)平面\(A_1C_1F\)，则直线\(DE//\)平面\(A_1C_1F\)。

求证(2)平面\(B_1DE\perp\)平面\(A_1C_1F\).

分析：\(\Leftarrow\)平面\(B_1DE\perp\)平面\(A_1C_1F\)

\(\Leftarrow\)一个面内的某条直线\(\perp\)另一个面内的两条相交直线。

此时往往需要结合图形及已知条件来确定，比如将一个面内的某条直线暂时确定为直线\(A_1F\)，

那么此时就需要在另一个平面\(B_1DE\)内找两条相交直线，且都要能证明和直线\(A_1F\)，

如果能找到，则这样的思路就基本固定下来了，

思路一大致为：\(A_1F\perp\begin{cases}B_1D\\DE\end{cases}\)，

从而转证\(DE\perp A_1F\)，从而转证\(A_1C_1\perp A_1F\)，

从而转证\(A_1C_1\perp\)包含\(A_1F\)的平面\(ABB_1A_1\)，

从而转证\(A_1C_1\perp\begin{cases}A_1B_1\\A_1A\end{cases}\)；

思路二大致为：\(B_1D\perp\begin{cases}A_1F\\ A_1C_1\end{cases}\)，

从而转证\(A_1C_1\perp B_1D\)，

从而转证\(A_1C_1\perp\)包含\(B_1D_1\)的平面\(ABB_1A_1\)，

从而转证\(A_1C_1\perp\begin{cases}A_1B_1\\ A_1A\end{cases}\)；

证明：你能自主写出证明过程吗？

【反思提升】上述解答中的思路一中，在分析需要证明\(A_1F\perp DE\)时，包含了视角上的转换，如证明\(A_1F\perp DE\)不容易时，我们转而证明\(DE\perp A_1F\)，即转证\(A_1C_1\perp A_1F\)，从而接下来就可以考虑证明线面垂直，从而转证\(A_1C_1\perp\)包含\(A_1F\)的平面\(ABB_1A_1\)，

体积求解

例3【2017凤翔中学第二次月考理科第19题】如图，\(\Delta ABC\)和\(\Delta BCD\)所在平面互相垂直，且\(AB=\)\(BC=BD\)\(=2\)，\(\angle ABC=\angle DBC=120^{\circ}\)，\(E、F、G\)分别是\(AC、DC、AD\)的中点，

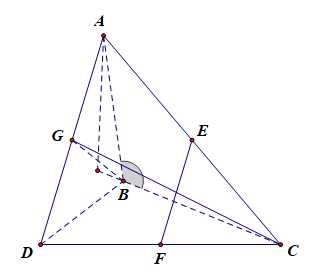
(1)求证：\(EF\perp 平面BCG\)

分析提示：只要证明\(AD\perp 平面BCG\)

(2)求三棱锥\(D-BCG\)的体积。

分析：在平面\(ABC\)内，作\(AO\perp BC\)，交\(CB\)延长线于\(O\)，由平面\(ABC\perp BCD\)，可知\(AO\perp 平面BDC\)，

由\(G\)到平面\(BCD\)距离\(h\)是\(AO\)长度的一半，在\(\Delta AOB\)中，\(AO=AB\cdot sin60^{\circ}=\sqrt{3}\)，

故\(V_{D-BCG}=V_{G-BCD}=\cfrac{1}{3}S_{\Delta DBC}\cdot h\)\(=\cfrac{1}{3}\cdot \cfrac{1}{2}\cdot BD\cdot BC\)\(\cdot sin120^{\circ}\cdot \cfrac{\sqrt{3}}{2}\)\(=\cfrac{1}{2}\)。

视角的转化

标签：image   lin   结合   com   反思   case   mic   alpha   span   

原文地址：https://www.cnblogs.com/wanghai0666/p/12905783.html