标签:追踪 solution target 算法 tar rom 思想 aik 分析
本问题被称为 荷兰国旗问题,最初由 Edsger W. Dijkstra提出。
其主要思想是给每个数字设定一种颜色,并按照荷兰国旗颜色的顺序进行调整。
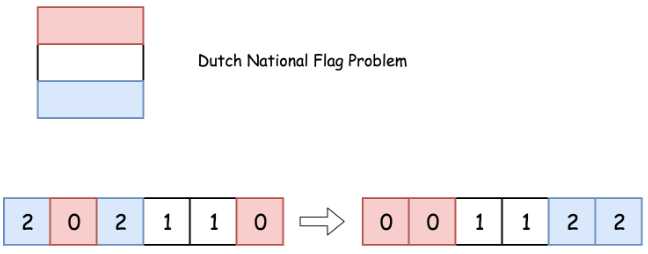
我们用三个指针(p0, p2 和curr)来分别追踪0的最右边界,2的最左边界和当前考虑的元素。
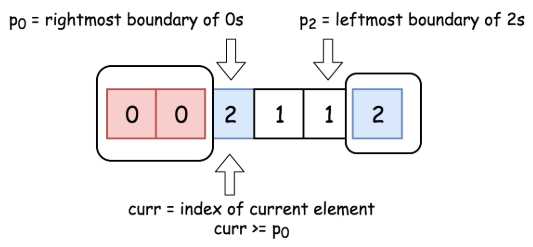
本解法的思路是沿着数组移动 curr 指针,若 nums[curr] = 0,则将其与 nums[p0]互换;若 nums[curr] = 2 ,则与 nums[p2]互换。
算法
初始化0的最右边界:p0 = 0。在整个算法执行过程中 nums[idx < p0] = 0.
初始化2的最左边界 :p2 = n - 1。在整个算法执行过程中 nums[idx > p2] = 2.
初始化当前考虑的元素序号 :curr = 0.
While curr <= p2 :
若 nums[curr] = 0 :交换第 curr个 和 第p0个 元素,并将指针都向右移。
若 nums[curr] = 2 :交换第 curr个和第 p2个元素,并将 p2指针左移 。
若 nums[curr] = 1 :将指针curr右移。
class Solution { /* 荷兰三色旗问题解 */ public void sortColors(int[] nums) { // 对于所有 idx < i : nums[idx < i] = 0 // j是当前考虑元素的下标 int p0 = 0, curr = 0; // 对于所有 idx > k : nums[idx > k] = 2 int p2 = nums.length - 1; int tmp; while (curr <= p2) { if (nums[curr] == 0) { // 交换第 p0个和第curr个元素 // i++,j++ tmp = nums[p0]; nums[p0++] = nums[curr]; nums[curr++] = tmp; } else if (nums[curr] == 2) { // 交换第k个和第curr个元素 // p2-- tmp = nums[curr]; nums[curr] = nums[p2]; nums[p2--] = tmp; } else curr++; } } }
复杂度分析
时间复杂度 :由于对长度 NN的数组进行了一次遍历,时间复杂度为O(N)。
空间复杂度 :由于只使用了常数空间,空间复杂度为O(1) 。
标签:追踪 solution target 算法 tar rom 思想 aik 分析
原文地址:https://www.cnblogs.com/ziytong/p/12909554.html