标签:spl pop 分配 main 答案 其他 reg -- 复杂度
题目描述:给定 \(n\) 个数 \(a_i\in[0,2^m)\),对所有 \(k=0,1,\dots,m\),求 \(\sum_{S\in \{a_i\}}[\text{popcount}(\bigoplus_{x\in S}x)=k]\)。
数据范围:\(n\le 2\cdot 10^5,m\le 53\)。部分分 \(m\le 35\)。
本文参考官方题解。
设 \(A\) 是给出的数得到的线性基,\(\text{span}(A)\) 表示 \(A\) 张成的线性空间, \(F(S)=\sum_{x\in\text{span}(S)}z^x\),\(P(S)=\sum_{x\in\text{span}(S)}z^{\text{popcount}(x)}\)。
设 \(\langle i,j\rangle=\text{popcount}(i\text{ and } j)\)。生成函数乘法默认 xor 卷积。
则 \(\langle i,k\rangle+\langle j,k\rangle\equiv \langle i\oplus j,k\rangle (\text{mod} \ 2)\),即乘法(and)关于加法(xor)的分配律。
首先大家肯定都会 \(O(2^{\text{rank}(A)})\),即枚举线性基的子集。
对于 \(m\le 35\),直接用 meet-in-the-middle,把线性基分成高位和低位两部分,其中低位部分只有在最低 $ \lceil\frac{m}{2}\rceil$ 位有值。设 \(f_{i,S}\) 表示对于高位的线性基异或出来的所有值,较高 \(\lfloor\frac{m}{2}\rfloor\) 位的 popcount 为 \(i\),较低 \(\lceil\frac{m}{2}\rceil\) 为 \(S\) 的方案数。\(g_S\) 表示低位的线性基异或出 \(S\) 的方案数。将 \(m\) 个 \(f_i\) 与 \(g\) 做 xor 卷积合并即可。复杂度 \(O(m2^{\lceil\frac{m}{2}\rceil}+m^22^{\lfloor\frac{m}{2}\rfloor})\)。
结果这个做法对满分做法没有一点用处(
满分做法使用了根号分治的思想,对于 \(\text{rank}(A)\le \lfloor\frac{m}{2}\rfloor\) 时使用暴力,对于其他情况考虑寻找一个 \(O(2^{m-\text{rank}(A)})\) 的做法。
有线性基的一些性质得到:
第一行:线性空间 做 线性空间内的线性变换 得到它自己。
第二行:乘法分配律。
第三、四行:做 FWT。根据这个柿子就可以知道,$\text{FWT}(F(A))$ 的每一位是 $0$ 或 $2^{\text{rank}(A)}$。
第五、六行:如果存在一个 $x$ 使得 $2\not|\langle k,x\rangle$,则该位不可能为 $2^{\text{rank}(A)}$,只能为 $0$。
定义 \(A\) 的正交线性基为 \(B\),使得 \(\forall x\in A,y\in B\),\(2|\langle x,y\rangle\)。并且 \(\text{rank}(A)+\text{rank}(B)=m\)。
则 \(F(B)\cdot 2^{\text{rank}(A)}=\text{FWT}(F(A))\)。
至于它怎么求,你可以把线性基中的列进行一些交换,使得它的左边是一个边长 \(\text{rank}(A)\) 的单位矩阵。
然后将右边一个矩形对称到它的左下方,右下方是一个边长为 \(m-\text{rank}(A)\) 的单位矩阵。
(放一个官方题解的图)
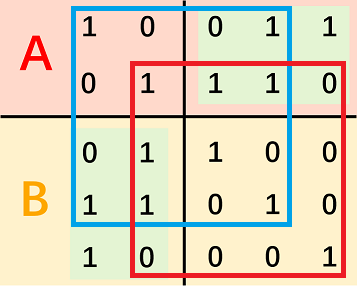
很容易检验它就是 \(A\) 的正交线性基,并且两两之间的 \(\langle x,y\rangle\in\{0,2\}\)。
求出正交线性基之后呢,考虑算答案。设 \(G_c=\sum_{x\ge 0}z^x[\text{popcount}(x)=c]\)。
我们知道 \(\text{FWT}(F(A))=F(B)\cdot 2^{\text{rank}(A)}\)。
(\(d\) 为枚举 \(F(B)\) 中每一项的大小,\(i\) 是 FWT 时的两个集合的交集大小)
直接计算,时间复杂度 \(O(2^{\lfloor\frac{m}{2}\rfloor}+mn+m^3)\)。
总而言之,正交线性基是一个与原线性基“互补”的东西,同时反映了原线性基的性质。也就找到了 \(O(2^{m-\text{rank}(A)})\) 的做法。
#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 63, mod = 998244353;
template<typename T>
inline void read(T &x){
int ch = getchar(); x = 0;
for(;ch < ‘0‘ || ch > ‘9‘;ch = getchar());
for(;ch >= ‘0‘ && ch <= ‘9‘;ch = getchar()) x = x * 10 + ch - ‘0‘;
}
template<typename T>
inline bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
inline bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
inline int ksm(int a, int b){
int res = 1; if(b < 0) b += mod - 1;
while(b){
if(b & 1) res = (LL) res * a % mod;
a = (LL) a * a % mod; b >>= 1;
}
return res;
}
inline void qmo(int &x){x += (x >> 31) & mod;}
LL lb[N], a[N], b[N], p[N];
int n, m, k, C[N][N];
inline void insert(LL x){
for(Rint i = m - 1;~i;-- i) if((x >> i) & 1){
if(!lb[i]){lb[i] = x; return;}
x ^= lb[i];
}
}
inline void dfs(int dep, LL x){
if(dep == k){++ p[__builtin_popcountll(x)]; return;}
dfs(dep + 1, x); dfs(dep + 1, x ^ a[dep]);
}
int main(){
read(n); read(m);
for(Rint i = 1;i <= n;++ i){
LL x; read(x); insert(x);
}
for(Rint i = 0;i < m;++ i)
if(lb[i]){
for(Rint j = i - 1;~j;-- j)
if((lb[i] >> j) & 1) lb[i] ^= lb[j];
}
for(Rint i = 0;i < m;++ i)
if(lb[i]){
for(Rint j = 0;j < m;++ j)
if(!lb[j]) a[k] = (a[k] << 1) | (lb[i] >> j & 1);
a[k] |= (1ll << m - 1 - k); ++ k;
}
if(k <= (m >> 1)){
dfs(0, 0); int tmp = ksm(2, n - k);
for(Rint i = 0;i <= m;++ i) printf("%lld ", p[i] * tmp % mod);
} else {
for(Rint i = 0;i < m - k;++ i){
for(Rint j = 0;j < k;++ j)
if((a[j] >> i) & 1)
b[i] |= (1ll << j);
b[i] |= (1ll << m - 1 - i);
}
swap(a, b); k = m - k;
dfs(0, 0); int tmp = ksm(2, n - m);
C[0][0] = 1;
for(Rint i = 1;i <= m;++ i){
C[i][0] = 1;
for(Rint j = 1;j <= i;++ j)
qmo(C[i][j] = C[i - 1][j] + C[i - 1][j - 1] - mod);
}
for(Rint c = 0;c <= m;++ c){
int ans = 0;
for(Rint d = 0;d <= m;++ d){
int tt = 0;
for(Rint i = 0;i <= c;++ i){
int ttt = (LL) C[d][i] * C[m - d][c - i] % mod;
if(i & 1) qmo(tt -= ttt);
else qmo(tt += ttt - mod);
}
qmo(ans += (LL) tt * p[d] % mod - mod);
}
printf("%lld ", (LL) ans * tmp % mod);
}
}
}
CF1336E Chiori and Doll Picking 【线性代数,组合计数】
标签:spl pop 分配 main 答案 其他 reg -- 复杂度
原文地址:https://www.cnblogs.com/AThousandMoons/p/12918990.html