最短路径问题

标签：通过   ++   动态   方便   计算   复杂度   无法   路径   搜索   

Floyd(弗洛伊德)算法

Floyed算法（时间复杂度为O(N3)，空间复杂度为O(N2)），是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题。

引例：

暑假，小哼准备去一些城市旅游。有些城市之间有公路，有些城市之间则没有，如下图。为了节省经费以及方便计划旅程，小哼希望在出发之前知道任意两个城市之前的最短路程。

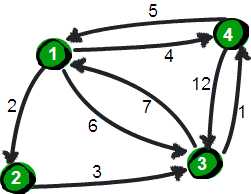
上图中有4个城市8条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程，也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。

我们可以用一个4*4的矩阵（二维数组e）来存储图的信息。比如：

• 1号城市到2号城市的路程为2，则设e[1][2]的值为2。
• 2号城市无法到达4号城市，则设置e[2][4]的值为∞。
• 另外此处约定一个城市自己是到自己的也是0，例如e[1][1]为0。

具体如下

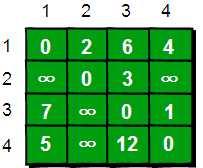
如果要让任意两点（例如从顶点a点到顶点b）之间的路程变短，只能引入第三个点（顶点k），并通过这个顶点k中转即a->k->b，才可能缩短原来从顶点a点到顶点b的路程。当然这个中转的顶点有时候甚至不止一个，即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市（4->3）的路程e[4][3]原本是12。如果只通过1号城市中转（4->1->3），路程将缩短为11（e[4][1]+e[1][3]=5+6=11）。其实1号城市到3号城市也可以通过2号城市中转，使得1号到3号城市的路程缩短为5（e[1][2]+e[2][3]=2+3=5）。所以如果同时经过1号和2号两个城市中转的话，从4号城市到3号城市的路程会进一步缩短为10。

因此，我们可以遍历每一个点作为中间点k，然后计算最小值

for (k = 1; k <= n; k++)
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            if (e[i][j] > e[i][k] + e[k][j])
                e[i][j] = e[i][k] + e[k][j];

也许有的人会有疑问，这样的遍历只遍历了中间点个数为1的情况，没有考虑中间点个数大于等于1的情况。其实不然，在计算中间点为k的最小值的时候，把能更新的元素都更新了，比如说更新了e[i][j]，这时候矩阵中第i行第j列的元素实际上是e[i][k]+e[k][j]，而不是e[i][j]了。这边用到了动态规划的思想。

总结下Floyed算法：

算法核心：每次引入一个点k来更新i到j最短距离，求出任意两点之间的最短距离。

基本步骤如下：

1. 从任意一条单边路径开始，所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。
2. 对于每一对顶点u和v，看看是否存在一个顶点w使得从u到w再到v比己知的路径更短，如果是更新它。
3. 对于所有的顶点，都重复上面的操作，直到遍历所有的顶点。

Dijkstra（迪杰斯特拉）算法

用于计算一个节点到其他节点的最短路径。 
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止

最短路径问题

标签：通过   ++   动态   方便   计算   复杂度   无法   路径   搜索   

原文地址：https://www.cnblogs.com/stu-jyj3621/p/12924651.html