K-periodic Garland from Codeforces Round #642 (Div. 3)E

标签：end   图片   从后往前   and   前缀和   一个   int   1的个数   continue   

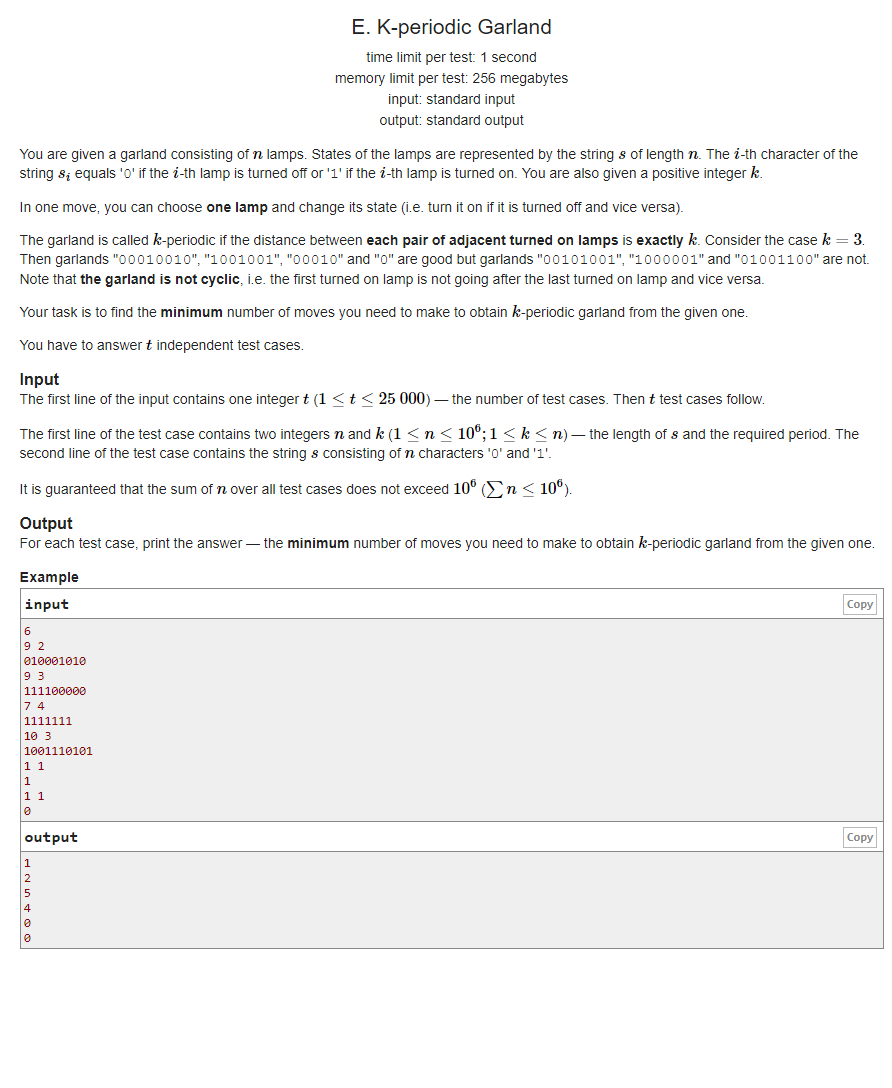
题目大意：给一个01串，可以将0变成1，1变成0，每次变换记为1次操作，问最终让每个1之前的距离都为k，需要最少多少次操作

数据范围1e6，很明显的一个复杂度o(n)的一个dp

做题思路是从已知的合法串递推出更长的合法串

首先处理左边到i位置为止左边所有位置合法的状态：dp(i) = min( sum[i-1] , dp[i-k] ) + ( i == ‘ 1 ‘ ? 0 : 1 ) ;

最终统计答案的时候再从后往前更新，让每一个dp(i)加上i之后1的个数，将i之后所有的1变成0，即为合法状态。

#pragma GCC optimize(2)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<string>
#define ll long long
using namespace std;
const int inf = 1e9;

int main()
{
    int t;
    cin >> t;
    string s;
    while (t--)
    {
        int n, k;
        cin >> n >> k;
        string s;
        cin >> s;
        s = ‘0‘ + s;
        vector<int>dp(n + 1, inf);//最初的dp数组中每个位置的操作数都不合法
        vector<int>sum(n + 1, 0);
        if (n == 1) { cout << "0" << endl; continue; }//特判n==1时的情况
        for (int i = 1; i <= n; i++)//预处理前缀和
        {
            sum[i] = sum[i - 1];
            if (s[i] == ‘1‘)
                sum[i]++;
        }
        //cout << endl;
        int ans = sum[n];//ans初始化为将所有1全部变成0

        //dp[i]记录到i位置位置全部合法所需要的操作数

        for (int i = 1; i <= n; i++)
        {
            dp[i]= sum[i - 1];
            if (i - k >= 1)
            {
                dp[i] = min(dp[i], dp[i - k] + (sum[i - 1] - sum[i - k]));
            }
            if (s[i] == ‘0‘)dp[i]++;
        }

        int num = 0;
        for (int i = n; i >= 1; i--)
        {
            ans = min(ans, dp[i] + num);//将i位置之后的1全部清除也得纳入答案决策内
            if (s[i] == ‘1‘)
                num++;
        }
        cout << ans << endl;
    }
    return 0;

}

K-periodic Garland from Codeforces Round #642 (Div. 3)E

标签：end   图片   从后往前   and   前缀和   一个   int   1的个数   continue   

原文地址：https://www.cnblogs.com/ruanbaiQAQ/p/12928322.html