标签：连线   官方   mic   sas   pre   point   name   题解   点积   

题目大意

题解

神仙题，完全想不到正解

半平面交乱搞：https://www.cnblogs.com/gmh77/p/12916223.html

暴力做法：枚举A中的两个点，判断圆心在中垂线上的区间

把(x,y)投影到抛物面x^2+y^2=z上，即(x,y,x^2+y^2)

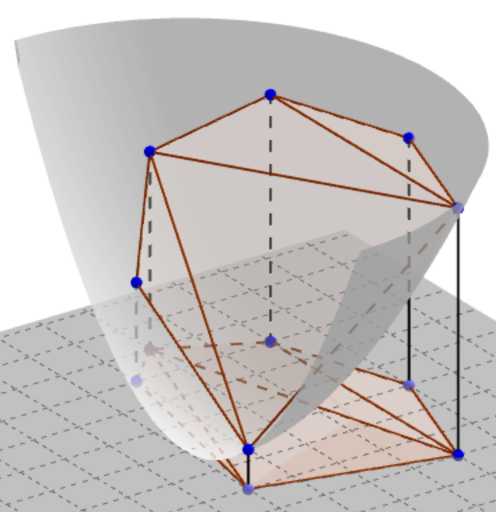
来自官方题解

那么一个平面ax+by+c=z和抛物面的交即x^2+y^2-ax-by-c=0，投影回二维平面上就是一个圆

由于这个抛物面是下凸的，所以在平面下方等价于在圆内，在平面上方等价于在圆外

于是问题变成了：找一个平面使得A点在平面下方，B点严格在平面上方

可以发现A在三维的上凸壳的点就是在二维上凸包的一个三角剖分，而暴力找两个点等价于把经过两个点连线的平面全部计算一遍

具体来说，对于上凸壳的一个面，上面的点一定在圆上，并且包住了A中的所有点

那么每次找凸包（不能有多余点）上两个相邻的点，在剩下的点中找一个最大的三点圆，这个圆一定包括了所有点，然后往两边分即可

这样显然不会算到非凸壳上的边，并且能分出一种方案，那么最后这种方案一定是合法的（可能有多种但不影响）

然后对凸壳上的每条边暴力做即可

二维整点的凸包点数是值域C的2/3次方别问我不会证，所以最终时间是O(C^(4/3)*(n+m))

关于圆心所在的计算：对余切进行约束即可，等价于对圆周角的余切进行约束

余切=点积/叉积

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define abs(x) ((x)>0?(x):-(x))
#define inf 2133333333
#define E 0.00000001
#define ll long long
//#define file
using namespace std;

struct point{double x,y;} a[10001],b[10001],d[10001],A[10001],B[10001];
struct xl{;double X1,Y1,X2,Y2;};
int n,m,N,M,i,j,k,l,mn2,t;
double mn,Mn,s,s1,s2,S1,S2,ss;

void swap(int &x,int &y) {int z=x;x=y;y=z;}
double cj(xl a,xl b) {return (b.X2-b.X1)*(a.Y2-a.Y1)-(a.X2-a.X1)*(b.Y2-b.Y1);}
double dj(xl a,xl b) {return (a.X2-a.X1)*(b.X2-b.X1)+(a.Y2-a.Y1)*(b.Y2-b.Y1);}
bool cmp(point a,point b) {double s=cj({0,0,a.x,a.y},{0,0,b.x,b.y}); return s<-E || abs(s)<=E && (a.x*a.x+a.y*a.y)<(b.x*b.x+b.y*b.y);}

void pd(int t1,int t2)
{
	int i,j,k,l;
	
	s1=inf;s2=inf;
	fo(i,1,t)
	if (i!=t1 && i!=t2)
	{
		s=cj({d[i].x,d[i].y,d[t1].x,d[t1].y},{d[i].x,d[i].y,d[t2].x,d[t2].y});ss=s;
		if (abs(ss)>E)
		{
			s=dj({d[i].x,d[i].y,d[t1].x,d[t1].y},{d[i].x,d[i].y,d[t2].x,d[t2].y})/s;
			if (ss>0) s2=min(s2,-s); else s1=min(s1,s);
		}
		else
		if (dj({d[i].x,d[i].y,d[t1].x,d[t1].y},{d[i].x,d[i].y,d[t2].x,d[t2].y})>E) return;
		
		if (s1+s2<E) return;
	}
	fo(i,1,m)
	{
		s=cj({b[i].x,b[i].y,d[t1].x,d[t1].y},{b[i].x,b[i].y,d[t2].x,d[t2].y});ss=s;
		if (abs(ss)>E)
		{
			s=dj({b[i].x,b[i].y,d[t1].x,d[t1].y},{b[i].x,b[i].y,d[t2].x,d[t2].y})/s;
			if (ss>0) s1=min(s1,s); else s2=min(s2,-s);
		}
		else
		if (dj({b[i].x,b[i].y,d[t1].x,d[t1].y},{b[i].x,b[i].y,d[t2].x,d[t2].y})<-E) return;
		
		if (s1+s2<E) return;
	}
	
	printf("YES\n");exit(0);
}

void dg(int x,int y)
{
	int i,j,k,l,mx;
	if (x+1>=y) return;
	
	if (x==1 && y==t)
	{
		s1=-inf;
		fo(i,2,t-1)
		{
			s=dj({d[i].x,d[i].y,d[1].x,d[1].y},{d[i].x,d[i].y,d[t].x,d[t].y})/cj({d[i].x,d[i].y,d[1].x,d[1].y},{d[i].x,d[i].y,d[t].x,d[t].y});
			if (s>s1) s1=s,mx=i;
		}
		pd(1,mx);pd(t,mx);
		dg(1,mx);dg(mx,t);
	}
	else
	{
		s1=-inf;
		fo(i,x+2,y)
		{
			s=dj({d[i].x,d[i].y,d[x+1].x,d[x+1].y},{d[i].x,d[i].y,d[x].x,d[x].y})/cj({d[i].x,d[i].y,d[x+1].x,d[x+1].y},{d[i].x,d[i].y,d[x].x,d[x].y});
			if (s>s1) s1=s,mx=i;
		}
		pd(x,mx);pd(x+1,mx);
		dg(x+1,mx);dg(mx,y);
	}
}

void work()
{
	int i,j,k,l;
	
	mn=inf;
	fo(i,1,n) if (a[i].y<mn || abs(a[i].y-mn)<E && a[i].x<Mn) mn=a[i].y,Mn=a[i].x,mn2=i;
	j=0;
	fo(i,1,n) if (i!=mn2) a[++j]={a[i].x-Mn,a[i].y-mn};--n;
	fo(i,1,m) b[i]={b[i].x-Mn,b[i].y-mn};
	
	sort(a+1,a+n+1,cmp);
	t=1;d[1]={0,0};
	fo(i,1,n)
	{
		while (t>1 && cj({d[t-1].x,d[t-1].y,d[t].x,d[t].y},{d[t-1].x,d[t-1].y,a[i].x,a[i].y})>=-E) --t;
		d[++t]=a[i];
	}
	
	if (t>3)
	{
		fo(i,1,t)
		{
			s=cj({d[i].x,d[i].y,d[i%t+1].x,d[i%n+1].y},{d[i%t+1].x,d[i%t+1].y,d[(i+1)%t+1].x,d[(i+1)%t+1].y});
			if (abs(s)<E) cout<<"???"<<endl;
		}
	}
	
	fo(i,1,t-1) pd(i,i+1);pd(t,1);
	if (t==2) pd(1,2);
	else
	if (t==3) pd(1,2),pd(2,3),pd(3,1);
	else
	dg(1,t);
}

int main()
{
	#ifdef file
	freopen("cf549E.in","r",stdin);
	#endif
	
	scanf("%d%d",&N,&M);
	if (N==1 || M==1) {printf("YES\n");return 0;}
	fo(i,1,N) scanf("%lf%lf",&A[i].x,&A[i].y);
	fo(i,1,M) scanf("%lf%lf",&B[i].x,&B[i].y);
	
	memcpy(a,A,sizeof(A));memcpy(b,B,sizeof(B));n=N,m=M;work();
	memcpy(a,B,sizeof(B));memcpy(b,A,sizeof(A));n=M,m=N;work();
	printf("NO\n");
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}

CF549E Sasha Circle

标签：连线   官方   mic   sas   pre   point   name   题解   点积   

原文地址：https://www.cnblogs.com/gmh77/p/12932470.html