下面这篇文章,感觉讲的非常好:
http://www.8btc.com/baizhantingjiangjun
拜占庭将军问题是一个共识问题: 首先由Leslie Lamport与另外两人在1982年提出,被称为The Byzantine Generals Problem或者Byzantine Failure。核心描述是军中可能有叛徒,却要保证进攻一致,由此引申到计算领域,发展成了一种容错理论。随着比特币的出现和兴起,这个著名问题又重入大众视野。
应该明确的是,拜占庭将军问题中并不去考虑通信兵是否会被截获或无法传达信息等问题,即消息传递的信道绝无问。Lamport已经证明了在消息可能丢失的不可靠信道上试图通过消息传递的方式达到一致性是不可能的。所以,在研究拜占庭将军问题的时候,我们已经假定了信道是没有问题的,并在这个前提下,去做一致性和容错性相关研究。如果需要考虑信道是有问题的,这涉及到了另一个相关问题:两军问题。
1.2.与拜占庭将军相关问题:两军问题
正如前文所说,拜占庭将军问题和两军问题实质是不一样的。国内大量解释拜占庭将军问题的文章将两者混为一谈,其实是混淆了两个问题的实质,由此造成了许多误解。这两个问题看起来的确有点相似,但是问题的前提和研究方向都截然不同。
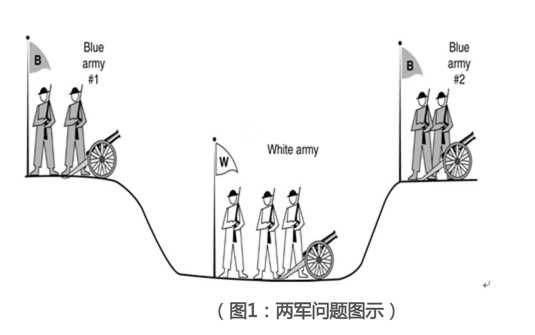
看到这里您可能发现两军问题和拜占庭将军问题有一定的相似性,但我们必须注意的是,通信兵得经过敌人的沟渠,在这过程中他可能被捕,也就是说,两军问题中信道是不可靠的,并且其中没有叛徒之说,这就是两军问题和拜占庭将军问题的根本性不同。由此可见,大量混淆了拜占庭将军问题和两军问题的文章并没有充分理解两者。
两军问题的根本问题在于信道的不可靠,反过来说,如果传递消息的信道是可靠的,两军问题可解。然而,并不存在这样一种信道,所以两军问题在经典情境下是不可解的.
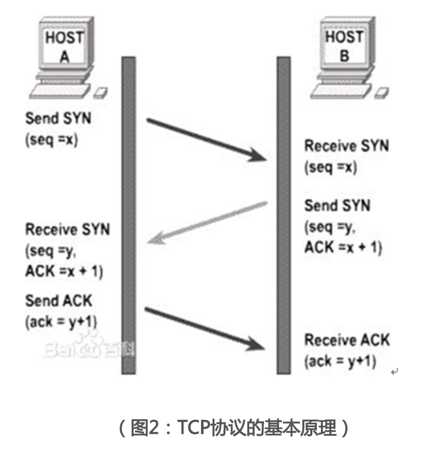
但我们能不能通过一种相对可靠的方式来解决大部分情形呢?这需要谈到TCP协议。事实上,搜索“两军问题与三次握手”,您一定可以找到大量与TCP协议相关的内容。
权当笔者是班门弄斧,这里仅用最浅显易懂的方式科普TCP协议的原理和局限,可能存在一些毛刺,请多包涵。
那么,是否能够找到一个理论方法来真正的破解两军问题呢?答案是有的,量子通讯协议,笔者并没有能力弄清这个颇为高深的问题。据我的理解,处于量子纠缠态的两个粒子,无论相隔多远都能够彼此同步,光是直观的来看,这个效应可以用来实现保密通讯。
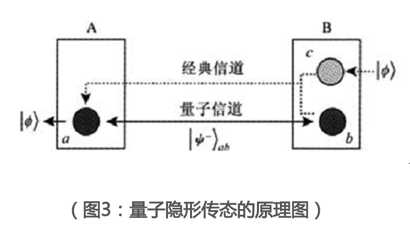
但是由于测不准原理,一测量粒子状态就会改变其状态,所以通讯时还必须通过不可靠信道发送另一条信息。尽管这个“另一条信息”是不可靠的,但是由于已经存在了一条绝对可靠的信道(量子纠缠),保证了另一条信道即使不可靠也能保证消息是可靠的,否则至少被窃取了一定能够被发现。
2.1. 拜占庭将军问题实质
至此,我们将拜占庭将军问题简化成了,所有忠诚的将军都能够让别的将军接收到自己的真实意图,并最终一致行动;而形式化的要求就是,
“一致性”与“正确性”。
2.2.形式化条件的推演
拜占庭问题,关键要达到下面两个目标:
IC1:所有忠诚的副官遵守一个命令,即一致性。
IC2:若司令是忠诚的,每一个忠诚的副官遵守他发出的命令,即正确性。
在经典的情形下,我们可以找到两种办法,口头协议和书面协议。笔者将会逐一探讨两种算法的推演和证明,其中证明部分并不会采用纯推理,而以介绍证明思路为主。
Part3:口头协议
首先,我们明确什么是口头协议。我们将满足以下三个条件的方式称为口头协议:
A1:每个被发送的消息都能够被正确的投递
A2:信息接收者知道是谁发送的消息
A3:能够知道缺少的消息
先告知结论:采用口头协议,若叛徒数少于1/3,则拜占庭将军问题可解。也就是说,若叛徒数为m,当将军总数n至少为3m+1时,问题可解(即满足了IC1和IC2)。
3.1.口头协议算法OM(m)
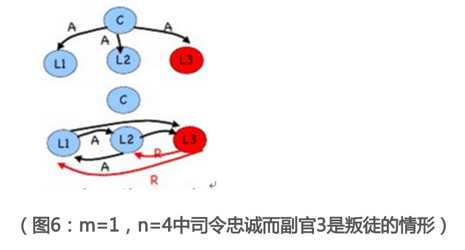
倘若司令在OM(1)中给各副官发送的消息都是进攻(A),之后OM(0)时,叛徒副官3给副官1和副官2说他收到的消息是撤退(R)。那么对于副官1(或副官2)来说,他综合司令、副官3和副官2(或副官1)后得到的消息向量都将会是(A,A,R),利用majority函数之后,将会采用A,满足了IC1和IC2(回顾IC1:所有忠诚的副官遵守一个命令,IC2:若司令是忠诚的,每一个忠诚的副官遵守他发出的命令)。
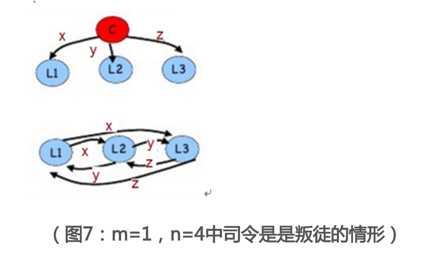
倘若司令是叛徒,那么我们已经不需要满足IC2。为方便,我们假设叛徒司令在OM(1)会给三个副官发送的信息是(x,y,z),其中x,y,z都可以是A或R的任意一种。之后,三位忠诚的副官将会按照OM(0)要求的那样,交换他们收到的信息。
对于副官1,他综合司令、副官2和副官3后得到的消息向量将会是(x,y,z),可以发现对于其他两个忠实的副官,他们得到的消息向量也将是(x,y,z)。不管x,y,z如何变化,majority(x,y,z)对于三人来说都是一样的,所以三个副官将会采用一致的行动。
(3)m=2,n=7的情形 接下来,我们将讨论m=2,n=7的情形,虽然只是多了一个叛徒,但是这里会出现递归过程,所以会复杂很多。
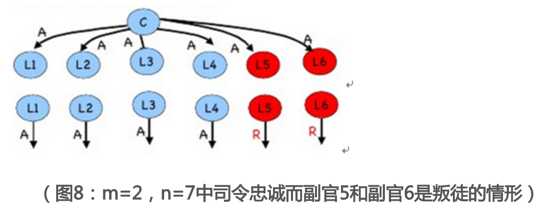
在OM(2)中,司令将攻击命令(A)传给各个副官。在OM(1)中,忠诚的副官们将会发送他们收到的消息(A),但由于副官5和副官6是叛徒,他们将会发送别的信息(比如R)。这时,忠诚的副官们将会采用使用OM(1)中的方法来确定各个v1~v6。例如,对于副官1,他收到了司令传来的命令,他会直接采用majority函数综合司令和其他将军传来的信息吗?他不会,因为这还在OM(1)中,他并不知道司令是不是叛徒,他会利用询问别人的方式来确认将军的命令,但是按照算法他会把司令的命令作为v1(即v1=A)并传给其他人。
接下来他会努力取得其他的v2~v6的值,这时已经在OM(1)中了,副官1绝不会轻易相信别人传来的消息,比如副官2给他传来了命令A,但是他会怀疑副官2传来的消息,所以他用OM(1)大法,问其他人副官2传给了他们什么,副官3和副官4诚实的告诉副官1(也就是所有人都要问到,都要听到),副官2给他们传的是A,而这时副官5和副官6又要撒谎了,他们又乱说,我们姑且假定他们传来的是x’和y’吧。这样,终于进入到了OM(0),这时副官1将会综合其他副官对于v2的反馈,得到向量(A,A,A,x’,y’),再利用majority函数,得到了v2=A。如下图,这是副官1在OM(1)中得到的信息(x,y等表示了不确定的命令)。
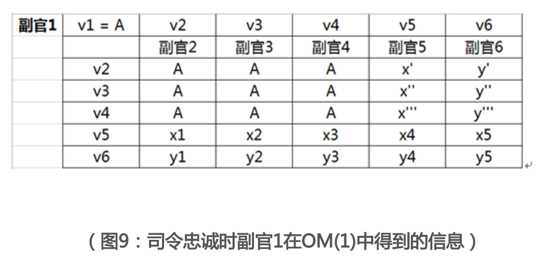
所以,我们可以发现忠诚的副官采用的命令都是A(满足IC1),并且和忠诚的将军的命令一致(满足IC2)。至此,您应该已经明白了这个算法是怎么递归的,不管m等于多少,都只是一个算法步骤多寡的问题。
至于司令是叛徒的情形,其实是相似的,这里简单的再提一下便于理解。若您已经明白了算法过程,完全可以跳过。

最终他们采用的行动都会是A(满足了IC1),而司令是叛徒不需要满足IC2。
我们回顾一下命题:
将军总数为n,叛徒数量为m,OM(m)可以实现,在n>3m(至少3m+1)的情况下,使得:
IC1:所有忠诚的副官遵守一个命令。
IC2:若司令是忠诚的,每一个忠诚的副官遵守他发出的命令。
Part4:书面协议
除了A1,A2和A3以外,我们在口头协议之上添加一个条件A4,使之成为书面协议
A4:(a)签名不可伪造,一旦被篡改即可发现,而叛徒的签名可被其他叛徒伪造;(b)任何人都可以验证签名的可靠性。
回顾A1-3:
A1:每个被发送的消息都能够被正确的投递
A2:信息接收者知道是谁发送的消息
A3:能够知道缺少的消息
那么,我们先说结论:对于任意m,最多只有m个背叛者情况下,算法SM(m)能解决拜占庭将军问题。也就是说,在使用签名的情况下,书面协议可以打破三模冗余的僵局,使用了签名的情况下,只要知道了叛徒数量,我们就可以利用SM(m)算法解决拜占庭将军问题。
4.1.书面协议算法SM(m)
笔者对书面协议尽量简短的介绍。回顾
IC1:所有忠诚的副官遵守一个命令,即一致性。
IC2:若司令是忠诚的,每一个忠诚的副官遵守他发出的命令,即正确性。
4.2.书面协议实例推演
举个例子,n=3,m=1,其中司令是叛徒,这是口头协议不能解决的状况。
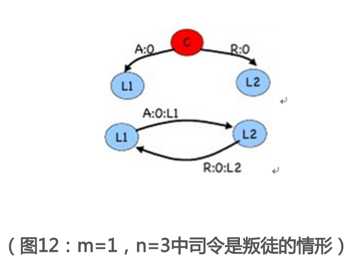
很显然,副官1得到的V1={A,R},副官2得到相同的V2={A,R}。他们采用choice函数后得到的命令一定相同。
回顾之前的口头协议,m=1, n=3是无法解决的。因为:
如果司令是叛徒,两个副官忠诚,司令会发送两个不同的命令。当两个副官对照命令时,他们又凌乱了,无法判断司令是叛徒或者对方是叛徒,从而又无法判断。这个情形非常简易的说明了三模冗余是无法动态容错的。
可以看出,OM无法处理三模冗余,是因为无法判断消息本来是司令乱发的,还是另一个副官篡改的。 而SM书面协议能够保证消息不被篡改,所以就OK了。
关键点就在于签名不可伪造。
相似的,n=4,m=2,其中司令是叛徒,这同样是口头协议不能解决的状况。
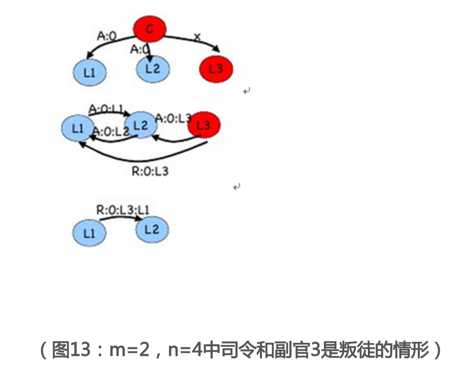
书面协议的本质就是引入了签名系统。
结论
书面协议的结论非常令人兴奋,这不是解决了拜占庭将军问题了吗?但请注意我们在A1~A4中实际上是添加了一些条件的,这使得拜占庭将军问题在这些假设下能够解决,但是在实际状况中却会有一些问题。观察A1~A4,我们做了一些在现实中比较难以完成的假设,比如没考虑传输信息的延迟时间,书面协议的签名体系难以实现,而且签名消息记录的保存难以摆脱一个中心化机构而独立存在。
回顾A1-A4:
A1:每个被发送的消息都能够被正确的投递
A2:信息接收者知道是谁发送的消息
A3:能够知道缺少的消息
A4:(a)签名不可伪造,一旦被篡改即可发现,而叛徒的签名可被其他叛徒伪造;(b)任何人都可以验证签名的可靠性。
