3D惯导Lidar仿真

标签：最小   导致   手动   可行性   环境   轨迹   imu   选择   结果   

 摘要             

提出了最近点平面表示的形式化方法，并分析了其在三维室内同步定位与映射中的应用。提出了一个利用最近点平面表示的无奇异平面因子，并在基于图的优化框架中证明了它与惯性预积测量的融合。所得到的LiDAR惯性三维平面SLAM（LIPS）系统在定制的LiDAR模拟器和实际实验中都得到了验证。

I.介绍

准确、鲁棒的室内定位和映射是自动机器人许多应用的基本要求。室内环境通常是丰富的指令信息，如直线和平面，应加以利用，以实现高精度的同时定位和制图（SLAM）。尽管在室内环境中使用GPS进行定位，惯性导航系统（INS）与外部处理传感器（如摄像机[1，2]、光探测和测距（LiDAR）传感器[3，4]甚至声纳[5]）的辅助已经被证明是有效。

最近激光雷达传感技术在重量和尺寸上都有所减少，允许便携式和手持使用，每秒在周围环境中提供220万个数据点。激光雷达已被证明是有效的纹理少和低光环境，典型的办公室和建筑内部，提供高信噪比（SNR）的测量。基本上，激光雷达传感器不依赖于其他传感器所需的照明或纹理特性。激光雷达传感器最具挑战性的一个方面是如何处理大量无序的三维点数据估计。传统的方法是使用迭代闭合点（ICP）解算器来确定两个点之间的相对变换。使用ICP只恢复相对姿态，防止在状态中包含信息量大的环境元素，如平面估计使用平面基元进行估计的第一个挑战是它们的参数化[6]。最常见的表示是平面的法向矢量和距离标量，称为黑森形式。自黑森形式是一个过度参数化，它将遭受一个奇异的信息矩阵在最小平方上他的工作是由特拉华大学（UD）工程学院部分支持，UD网络安全倡议、NSF（IIS-1566129）和DTRA（HDTRA1-16-1-0039）。为了避免这种过度参数化，通常使用包含两个角（水平角和垂直角）和一个距离标量的球面坐标作为其误差状态表示。虽然这是最小的，但当垂直角等于±π2时，它会有歧义。最近，Kaess[6]提出使用单位四元数及其无奇异性的3自由度乘性误差状态，该状态与平面的几何联系不清楚，其数值稳定性可能不是最优的。相比之下，在这项工作中，本文使用最接近的点（CP）来表示，这是由平面上最接近的点定义的，以确定给定的参考系。

本文的主要贡献如下：             

•最近点（CP）平面表示法的制定、奇点分析及其作为平面表示法和三维平面SLAM误差状态的使用。             

•设计一种新的激光雷达惯性三维平面SLAM（LIPS）系统，该系统具有基于图形优化的鲁棒相对平面锚定因子，有效地克服了CP表示的奇异性问题。             

•开发一个通用的激光雷达模拟器，用于评估激光雷达辅助定位算法，该模拟器是开源的，可以更好地造福社区。             

•通过蒙特卡罗模拟和实际实验验证提议的LIPS系统。

A. 基于图的优化

建立优化问题并迭代求解：

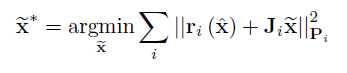
  B. LIPS系统

在LIPS系统中，定义每个时刻机器人的的状态为16*1维向量：

LIPS系统的最终的cost函数可以描述为：

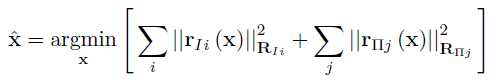
 C. 连续IMU预积分因子

最终的测量残差如下：

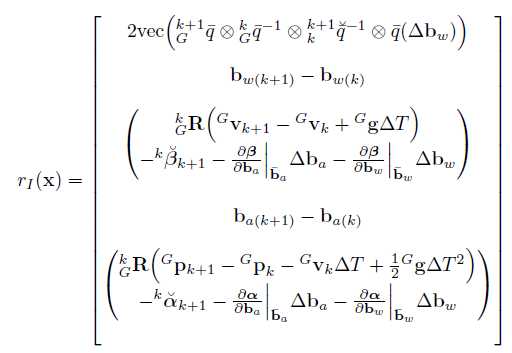
 D.最近点平面表示

“最近点（CP）”表示可以被描述为驻留在平面上并且最接近当前帧的原点的3D点。 这种表示的好处在于它已经处于其最小的表示中，并且如果特别注意选择它所定义的参考系，则它是单一的，无奇点。 通过将平面表示为单个3D点，在优化期间更新参数时也有一个简单的加性误差模型。 可以使用Hesse法向量和距离标量来描述该CP表示：

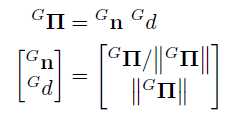
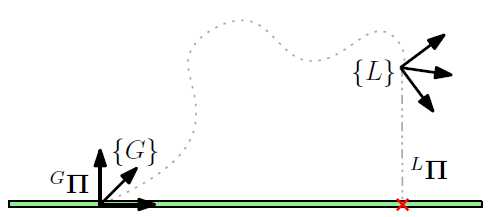
 图1：平面上最近点的直观表示

F.锚面因子

为克服CP表示的奇点问题，在第一观察帧中对平面进行参数化，保证到平面的距离将是非零的（从此处向后，这将表示为“锚”帧/状态）。如图2所示，从一帧到另一帧的平面表示变换不是直接的3D点变换，而是需要在新帧中计算CP。 使用Hesse平面表示，可以将锚坐标系{A}中表示的平面映射到局部坐标系{L}中，如下所示：

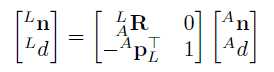
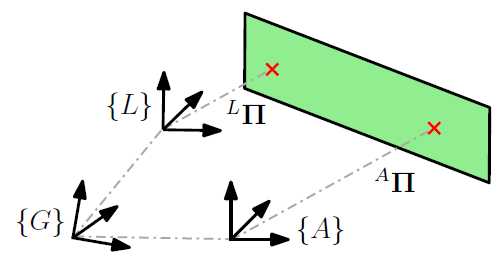
 图2：在局部{L}坐标系中看到的最近点平面表示的图示视图

G.点到平面的压缩

为了找到对应于平面的无序点云的子集，可以使用RANSAC或其他平面分割方法。

首先将提取的点子集压缩为本地CP并匹配可用于优化的协方差。可以从制定加权最小二乘优化问题开始，寻求最小化提取点与本地CP测量值Lп之间的点到平面距离：

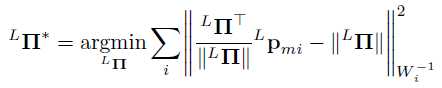
 计算最终局部最近点的协方差矩阵：

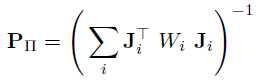
 主要结果

A. LiDAR惯性模拟器

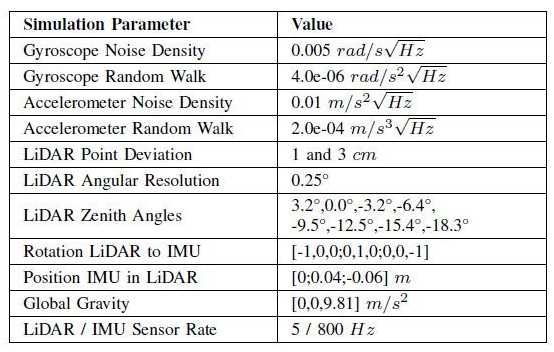
为了评估所提出系统的可行性，开发了定制的LiDAR IMU模拟器。创建了2D平面图并垂直拉伸以创建曼哈顿世界环境（为清楚起见，注意到CP表示可以处理任意平面方向）。一组有序的3D控制点用于通过环境创建3D样条轨迹。使用分析样条分化，可以在轨迹上的任何时间获得真实的IMU测量。在给定的LiDAR感测频率下，使用由角分辨率和垂直天顶角定义的固有LiDAR传感器模型生成光线。然后，生成的光线与环境中的所有平面相交，并找到所有光线平面交叉点。最后一步通过强制执行每条光线只应击中最接近LiDAR帧的平面来执行因遮挡而不应生成的交叉点的无效。

表1：模拟中使用的现实参数

 B.蒙特卡洛仿真

在不同的LiDAR噪声值下进行了80次LIPS系统的Monte-Carlo模拟，其结果如图4和表2所示。 所提出的CP表示和锚平面因子能够在不同水平的LiDAR传感器噪声下以高精度定位在平面环境中。 模拟是在实时完成的，平面对应已知并使用iSAM2解决。 朝向开始的大的非零定向误差是由于传感器在初始化之后保持静止一段时间，仅有少量远离平面约束定向。

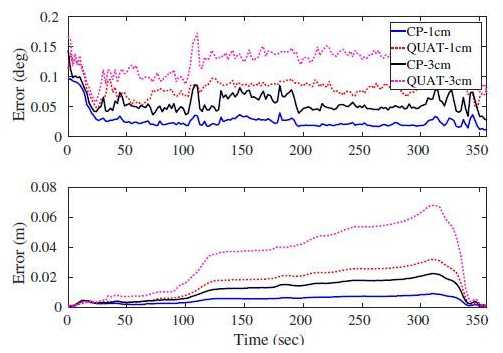
 图3：使用3D点作为输入的竞争基线的平面分割精度。地面真值深度图或推断深度图(由基于DNN的系统)作为它们的输入。PlaneNet优于使用推断深度图的所有其他方法，PlaneNet甚至比其他使用地面图的方法还要好。

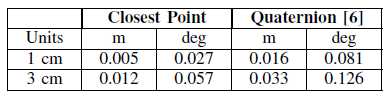
表2：在不同的LiDAR噪声值下，平均RMSE超过80次蒙特卡罗模拟

 由于进出房间，模拟轨迹的开始具有有限量的环闭合，导致估计误差增加，如通常在测距系统中看到的那样（参见图4）。 在300秒之后，轨迹重新进入长走廊并返回到起始位置，重新观察先前看到的走廊部分。 如图4所示，具有先前平面的循环闭合迅速将估计误差减小到零。

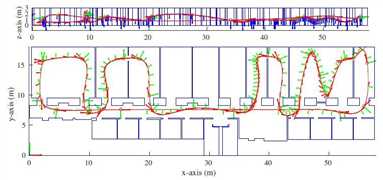
 图4：通过3D环境生成180米长的模拟轨迹。 原始的二维平面图（底部）已被挤压，并且样条曲线适合控制点以生成完整的轨迹。 轨迹从左上角开始，在距离地板不同高度的房间内进出，然后最终重新进入走廊并返回起始位置。

C.平面表示比较

CP表示在其四元数对应物上产生了改进的准确度。虽然此处显示的结果是使用iSAM2求解器生成的，但发现在完整批次优化期间，与CP相比，四元数表示收敛速度较慢。对这些结果的猜想是，基于CP的测量模型具有比四元数参数化更好的线性高斯近似，因此提供了更好的数值性能。

D.真实世界实验

在这个测试中，平面物体放置在LiDAR传感器周围，以便于RANSAC提取，避免退化运动[38]，并确保LiDAR在所有自由度上完全受约束。 使用以10Hz工作的八通道Quanergy M8 LiDAR，其中Microstrain 3DM-GX3-25 IMU连接到以500Hz工作的LiDAR底部。 手动估算了LiDAR到IMU的外部转换，但这可以很容易地添加到因子图中进行在线估算。 为了评估估计漂移，传感器单元在平面表面前移动并返回到相同的起始位置。在30米轨迹距离之后，起始和终止姿势之间的差异为1.5厘米，对应于轨迹长度上的0.05％误差。

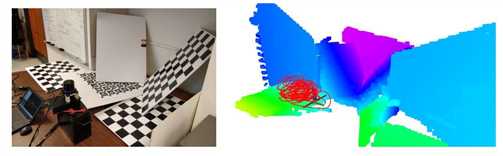
 图5：所提出的定位操作的实验环境（左）和平面的重建深度图（右）

3D惯导Lidar仿真

标签：最小   导致   手动   可行性   环境   轨迹   imu   选择   结果   

原文地址：https://www.cnblogs.com/wujianming-110117/p/12940840.html