标签:font 哈夫曼 tps img 字符 出现 节点 更新 计算
哈夫曼树(最优二叉树)
其目的:
找出存放一串字符需要的最少的二进制编码
构造方法:
1.得到每种字符出现的频率或者概率,即权值,构成频率表
2.找出频率最小的两个,小的在左边,大的在右边,组成二叉树。父节点为两者的和(不计入WPL计算),频率表更新(删除这两个数,同时加入两数的和)
3.重复2.
4.最后标记01,0左1右,每个字符的二进制表示从上到下读出。
详细例子:
https://blog.csdn.net/qq_29519041/article/details/81428934
总结:频率高的字符编码越短。
带权路径长度计算:
权值*深度求和。
比如下面这个树:
频率表:3 5 7 8 11 14 23 29
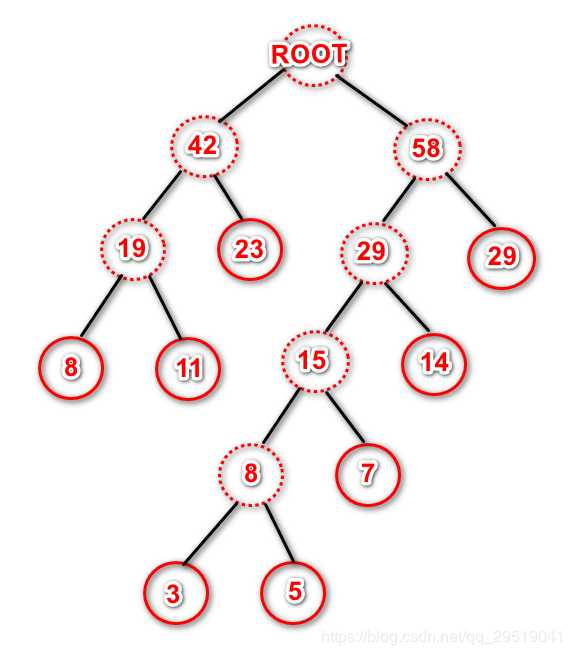
wpl=(3+5)*5+7*4+(8+11+14)*3+(23+29)*2=271
标签:font 哈夫曼 tps img 字符 出现 节点 更新 计算
原文地址:https://www.cnblogs.com/vera-7c/p/12941409.html