滤波器开发之二：基于算数平均的带阻平滑滤波器

标签：并且   总结   strong   最大数   处理流程   不同   替换   若是   size   

　　信号采集是非常常见的需求，我们也总是希望采集到的数据是纯净而真实的，但这只是我们的希望。环境中存在太多的干扰信号，为了让我们得到的数据尽可能地接近实际值，我们需要降低这些干扰信号的影响，于是就有了滤波器的用武之地。这里我们讨论的主要是软件实现的数字滤波器，这一篇我们就来讨论基于递推算术平均算法的带阻平滑滤波器。

1、问题的提出

　　我们已经实现了基于算术平均的递推算术平均滤波器。虽然它对周期性干扰和高频的干扰都有一定的效果，但是对于这种滤波器其灵敏度和滤波效果很难同时达到较好的效果。一般来说，当N值较小时，灵敏度会增高但滤波效果则不太理想；当N值较大时，滤波效果会比较好，但灵敏度会受到影响。所以我们希望能找到一种方法，让灵敏度和滤波效果都能有较好的表现。

　　关于这个问题，我们先来分析一下。一般来说，不管是周期性干扰还是噪声干扰都是在一定的范围内对数据造成影响。不会出现很大幅度的数据差异。基于这一点我们可以考虑对比本次采集与上次输出之间的偏差值，如果偏差值大于一定的限值则我们认为是数据发生了较大变化，远大于干扰造成的影响，干扰可以忽略，所以我们直接对数据进行更新。当数据偏差处于一定的变化范围之内时，我们认为是处于稳定的范围内，这时干扰造成的影响于数据的变化不能忽略，我们需要采用滤波。具体如图所示：

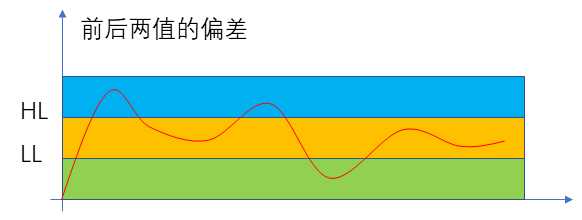
　　其中HL和LL就是我们之间的范围就是可能干扰不能忽略的范围；而大于HL的部分我们认为采集数据变化远超干扰的影响，忽略干扰提高灵敏度；而小于LL的部分说明干扰造成的影响很小，在允许的误差范围之内或者说在数据的正常波动范围之内，我们也不需要滤波。

　　我们在数据的变化大于干扰所能引起的数据差异时，选择不滤波而是快速更新数据以提高灵敏度。可是如果有一个偶然的脉冲干扰出现时，这种操作方式则会导致系统失效，所以我们必须引入消抖操作。当连续出现多个值都是大范围变化时，我们认为是数据的正常变化，否则我们认为是偶然的脉冲干扰造成的。

2、算法设计

       我们已经描述了在不同的偏差区间对采集数据采取不同处理方式的办法。具体怎么设计这一滤波算法呢？首先我们需要根据经验或者基于对被控对象的判断来确定HL和LL的范围，这样在不同范围内采取不同的处理方式的做法才能达到良好的效果。

　　我们先来看偏差处于HL和LL之间时该怎么处理。同样需要定义一个长度为N的数据队列。和前一篇中所说的一样，当采集到一个新的数据时，用这个新的数据替换掉最老的数据。并且将数据指针指向下一次需要替换掉的最老数据。然后使用队列中的数据去算术平均值而得到最新的输出数据，具体队列如下：

　　若是偏差落在大于HL和小于LL的范围内，则不需要滤波，该如何处理呢？我们一样需要数据队列，因为数据随时有可能回归到需要滤波的范围，我们必须每次的更新数据队列即使没有滤波需求。这时的更新数据方式不同，我们将整个队列的数据都替换为新数据，但我们不更新数据指针。输出数据就是本次采集的数据，具体的数据队列如下：

　　但是偏差落在大于HL和小于LL的范围内并不能直接更新数据队列的全部数据，因为可能是偶然性的脉冲干扰，我们需要作消抖处理。我们判断如果连续多少个的采集数据均落在相应的区间，我们就认为不是偶然的脉冲干扰。这是我们就更新队列的全部数据。

3、代码实现

　　我们已经设计了带阻区间滤波的相关算法，接下来我们来考虑如何实现这一滤波器。同样的，我们需要定义一个滤波器对象然后基于这一对象实现相应的滤波器操作。

　　我们先来分析一下，首先滤波器对象需要获取当前采集到的数据值；同时我们为了实现对N个数据的递推平均就需要有一个存储这N个数的队列；我们需要记录最新的数据硬件存储到哪个位置就需要一个位置指针；同时我们也需要知道N的大小，所以我们将它们都定义滤波器对象的属性。平滑滤波的过程必须要计算算术平均值，而递推算术平均则是在每次采集一个数据之时都计算平均值，可是如果N值较大时，就会存在大量的重复计算。我们考虑到上一次采样的平均值已经得到，我们将其记录下来的话就可以用最新采集的数据替换掉最老的数据，从而得到新的平均值，所以我们将上一时间的输出值记录下来作为对象的一个属性。除此之外，我们还需要知道滤波器的限制区间，即HL和LL，所以我们将采集数据所对应的量程范围、上限（HL）、下限（LL）比例均作为对象的属性。同时为了实现消抖，我们需要记录数据大幅变化的持续数及确认消抖的最大数值，这两个也作为对象的属性。根据以上分析我们可定义滤波器对象类型为：

 1 /*定义平滑滤波对象类型*/
 2 typedef struct FilterObject{
 3   float newValue;       //最新测量值
 4   float lastValue;      //上一个输出值
 5   float *buffer;        //数据缓存区
 6   int16_t position;    //写操作位置指针
 7   uint16_t bufCount;    //滤波的数量
 8   uint16_t delayCount;  //延迟计数
 9   uint16_t delayLimit;  //延迟限值
10   float rangeLimit;     //量程范围
11   float upperRario;     //比例下限
12   float lowerRatio;     //比例下限
13 }FilterObjectType;

　　我们已经获得了滤波器对象，接下来将基于这一对象实现相应的滤波器功能。我们要对比当前的采集值与上一个输出值的比较，根据它们的偏差绝对值来决定采取怎样的处理方式。处理流程如下：

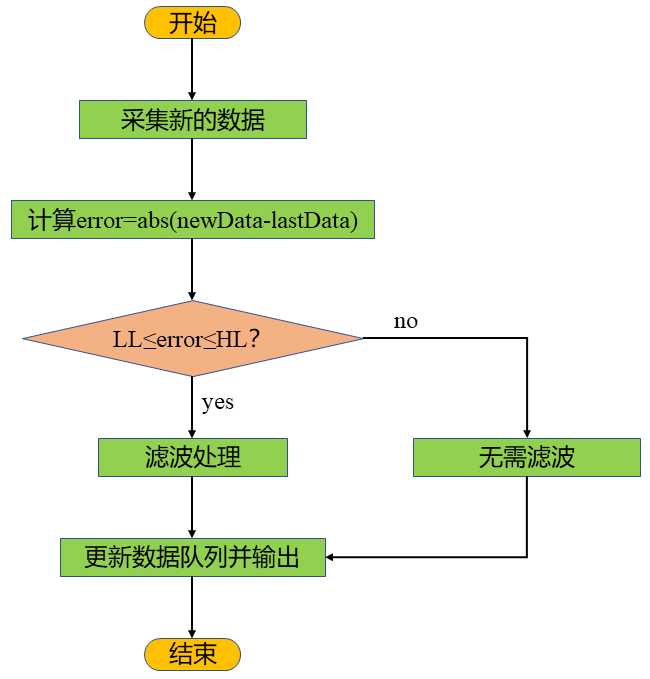
　　我们通过判断新值与前一个值的偏差来决定所要进行的操作，当偏差处于HL和LL之间时做滤波处理，否则不做滤波处理。根据以上的分析及流程图我们可以设计带阻平滑滤波器的代码为：

 1 /* 带阻平滑滤波器，对指定区间滤波，返回滤波后的值*/
 2 float BandSmoothingFilter(FilterObjectType *filter)
 3 {
 4   float result=filter->lastValue;
 5  
 6   if(filter->position<0)
 7   {
 8     for(int i=0;i<filter->bufCount;i++)
 9     {
10       filter->buffer[i]=filter->newValue;
11     }
12     filter->position=0;
13     filter->lastValue=filter->newValue;
14   }
15   
16   if(filter->position>=filter->bufCount)
17   {
18     filter->position=0;
19   }
20  
21   if(fabs(filter->newValue-filter->lastValue)>(filter->rangeLimit*filter->upperRario/100))
22   {
23     filter->delayCount+=1;
24     if(filter->delayCount>=filter->delayLimit)
25     {
26       for(int i=0;i<filter->bufCount;i++)
27       {
28         filter->buffer[i]=filter->newValue;
29       }
30       filter->position++;
31       result=filter->newValue;
32       filter->delayCount=0;
33     }
34   }
35   else if(fabs(filter->newValue-filter->lastValue)>=(filter->rangeLimit*filter->lowerRatio/100))
36   {
37     result=filter->lastValue-filter->buffer[filter->position]/filter->bufCount;
38    
39     result=result+filter->newValue/filter->bufCount;
40    
41     filter->buffer[filter->position++]=filter->newValue;
42    
43     filter->delayCount=0;
44   }
45   else
46   {
47     filter->delayCount+=1;
48     if(filter->delayCount>=filter->delayLimit)
49     {
50       for(int i=0;i<filter->bufCount;i++)
51       {
52         filter->buffer[i]=filter->newValue;
53       }
54       filter->position++;
55       result=filter->newValue;
56       filter->delayCount=0;
57     }
58   }
59   filter->lastValue=result;
60   filter->newValue=0.0;
61   return result;
62 }

4、应用总结

　　我们实现了基于算术平均的带阻平滑滤波器。该滤波器对周期性干扰和小幅的噪声干扰均有较好的效果。而且通过区间滤波，在数据快速变化时也提高了系统的灵敏度。对于干扰对数据的影响处于一定范围内的系统有很好的效果。

　　这一滤波器有效的前提是基于干扰的幅度并不是很大的前提而实现的。如果系统存在较大幅度的脉冲干扰，在这种脉冲干扰的出现频率较低时，消抖操作能够很好的去除这种偶然性干扰。但如果出现持续性的高频大幅脉冲干扰，这一滤波器将变得无能为力。

　　对于限值区间HL和LL的取值一般只能根据采集系统的特点或者工程师的经验来判断，这个取值决定了滤波器的滤波效果。

欢迎关注：

滤波器开发之二：基于算数平均的带阻平滑滤波器

标签：并且   总结   strong   最大数   处理流程   不同   替换   若是   size   

原文地址：https://www.cnblogs.com/foxclever/p/12941422.html