918. Maximum Sum Circular Subarray

标签：解法   pre   方便   结果   ati   cto   有一个   example   put   

问题：

给定一个数组，其为循环数组（最后一个元素的下一个元素为第一个元素）。

求连续子数组和的最大值。

Example 1:
Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:
Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:
Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:
Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:
Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1
 

Note:
-30000 <= A[i] <= 30000
1 <= A.length <= 30000

解法：

这里用到

53. Maximum Subarray

的算法kadane‘s algorithm

即：动态规划DP

动态转移方程：

dp[i]：到第i个元素，包含该元素A[i]的连续子数组最大和 curMax

dp[i]=max(dp[i-1]+A[i], A[i])

解释：若到上一个元素的连续子数组最大和为负值，那么肯定只选A[i]本身作为最大和。否则上一个最大值+A[i]（因为要到A[i]为止，包含A[i]）。

然后，要在求的所有连续子数组的最大和。

allMax

=max(到每一个元素为止连续子数组的最大和) = max(curMax)

=max(dp[0]~dp[n])

接着，解决本问题的循环数组特性。

要求的最大和Max subarray有以下两种情况：

Case1：在单次数列内部

Case2：跨越数列首尾

如下图所示：

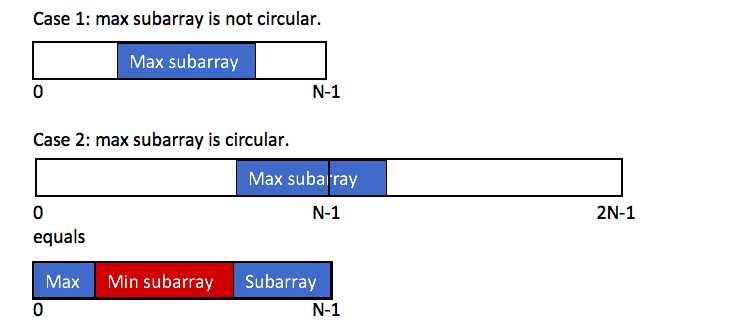
 为了方便计算，我们只循环单次数列：0～size

同时求的Max subarray和Min subarray的和allMax，allMin

那么，最后的结果则是：res=max(allMax, sum-allMin)

??注意：这里有一个特殊情况：若数列全都是负值，

那么allMax=Max(A[i])，allMin=sum

这时

res=max(allMax, sum-allMin)

=max(Max(A[i]), sum-sum)=0

含义为：Max subarray为空数组。

显然不满足题意。

因此，在这种情况下，我们要求的最大和，只能是Max(A[i])=allMax

代码参考：

 1 class Solution {
 2 public:
 3     int maxSubarraySumCircular(vector<int>& A) {
 4         int sum=A[0];
 5         int curMax=A[0], curMin=A[0], allMax=A[0], allMin=A[0];
 6         for(int i=1; i<A.size(); i++){
 7             //DP：curMax到i为止，最大和。=max(上一个最大和curMax+当前值A[i], A[i])
 8             curMax=max(A[i], curMax+A[i]);//到目前为止最大和curMax若为负数，那么新的最大和=A[i]
 9             allMax=max(allMax, curMax);//求到各个元素为止，最大和curMax，里的最大。
10             curMin=min(A[i], curMin+A[i]);
11             allMin=min(allMin, curMin);
12             sum+=A[i];
13         }
14         if(sum==allMin) return allMax;
15         return max(allMax, sum-allMin);
16     }
17 };

918. Maximum Sum Circular Subarray

标签：解法   pre   方便   结果   ati   cto   有一个   example   put   

原文地址：https://www.cnblogs.com/habibah-chang/p/12943511.html