第三单元总结

标签：技术   算法思路   效果   自动化测试   自己   比较   验证   自己的   学习   

1.理论基础

这次接触了JML————进行规格化设计的一种语言，用来表示一个接口要干些什么事，相比直接用文字叙述，这样的方式更加规范，不会千人千面，读起来也不会很费劲，我一般是猜测它想要干什么，再去细读是不是我想的那样，以下列举一下JML的规范：

• 原子表达式
  \result：表示返回值。
  \old(expr)：表示表达式expr在相应方法执行前的取值。
  \not_assigned(x,y,...)：用来表示括号中的变量是否在方法执行过程中被赋值。如果没有被赋值，返回为true，否则返回false。
  \not_modified(x,y,...)：该表达式限制括号中的变量在方法执行期间的取值未发生变化。
  \nonnullelements(container)：表示container对象中存储的对象不会有null。
  \type(type)：返回类型type对应的类型(Class)，如type(boolean)为Boolean.TYPE。TYPE是JML采用的缩略表示，等同于Java中的 java.lang.Class。
  \typeof(expr)：该表达式返回expr对应的准确类型。如\typeof(false)为Boolean.TYPE。
• 量化表达式
  \forall：全称量词修饰的表达式，表示对于给定范围内的元素，每个元素都满足相应的约束。
  \exists：存在量词修饰的表达式，表示对于给定范围内的元素，存在某个元素满足相应的约束。
  \sum：返回给定范围内的表达式的和。
  \product：返回给定范围内的表达式的连乘结果。
  \max：返回给定范围内的表达式的最大值。
  \min：返回给定范围内的表达式的最大值。
  \num_of：返回指定变量中满足相应条件的取值个数。
• 类型规格
  invariant：在所有可见状态下都必须满足的特性。
  constraint：对前序可见状态和当前可见状态的关系进行约束。
• 方法规格
  require：前置条件
  ensure：后置条件
  assignable：可赋值的
  modifiable：可修改的
  pure：仅查询
  signals：抛出异常

2.工具链

JML相关的工具链有OpenJML、jmlunitng

• OpenJML
  OpenJML最基本的功能就是对JML注释的完整性进行检查。检查包括经典的类型检查、变量可见性与可写性等。通过命令行使用OpenJML时，可以通过-check参数（缺省）指定类型检查。
• jmlunitng
  jmlunitng结合OpenJML可以自动化生产测试用例对代码进行测试
• junit
  junit也是老师们大力推荐的工具，在工业界也用的比较多，它像一个平台，我们可以人为构造测试用例对某些方法等进行测试，有比较完整的测试手段，用起来也比较灵活

3.自动化测试

利用jmlunitng结合OpenJML，我针对Group接口实现了自动测试，最终效果如下：

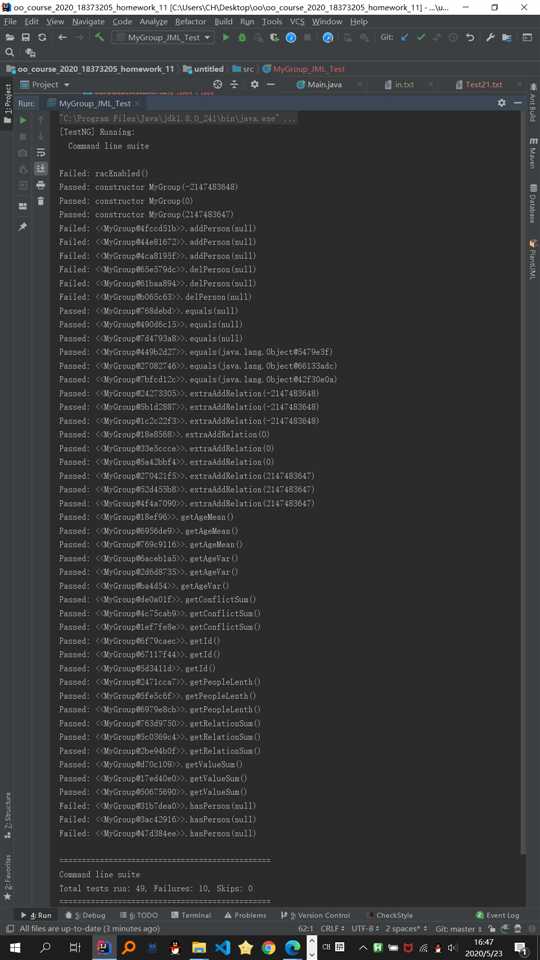
可以看见，由于是自动生产的用例，灵活性、适应性比较差，都是一些边界数据，如0、int的最大值之类的，包括传入引用时的null，缺少一般性的验证，有几个没有通过的点都是因为和我们的需求不太相符，某些方法未对传入引用判断其是否为空，当然判断最好，但不判断也可以保证我们的程序不出问题。当然我觉得既然是自动的，能做到这样已经很不错了。

4.架构设计

大的架构课程组都已经给出了，我不过是用了一下接口，实现了方法，下面针对几次作业的重点问题介绍一下我的写法

第一次作业

• isCircle
  第一次作业的难点就在这个函数了，简单来讲就是判断图中两个点的连通性，当然最直接的就是搜索算法，时间上也还好，对外的修改比较少，我个人习惯写BFS，因此采用了广度搜索算法来解决，不过后面的作业发现这个实现其实有些冗余的地方，特别是中间的容器使用。

第二次作业

• sum
  第二次作业增加了很多求和的操作，在性能上也有一些要求，所以我都采用了在外部设计一个变量来记录的方式，当加人、加关系的时候对它们的值进行修改，由于不会删人，这样的实现能保证性能最优。
• ageVar
  有一个需要好好考虑的就是这个求组内人年龄方差的问题，主要的问题在于规格要求用int计算，而我们的算法是有关外部的成员变量（比如年龄的平方和）的，计算公式有出入，那么就要考虑溢出、精度等问题，以免算出的结果和预期不符。

第三次作业

• blockSum
  求连通块的个数，当然最容易想到的就是采用并查集的方式，而且这种算法为其他方法判断联通提供了有利支持，我借鉴了网络上一些处理并查集的方式，最终采用一种树状结构来处理并查集，并入的复杂度为O(1)，每次查询都会更新人结点指向根节点，比起一般的并查集（并入复杂度为O(n)）,这样的方式避免了无效的并入，只会比一般的并查集操作性能更好。
• strongLink
  首先用BFS（BFS能保证找到的路径节点数最小）找到一条路径，挨个删除路径上的点并继续用BFS判断删除后是否连通，如果都连通则返回真，否则返回假，这样的算法思路来源于离散数学中对双连通分量的定义：若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。一个无向图中的每一个极大点（边）双连通子图称作此无向图的点（边）双连通分量。
• del
  好在作业仅要求对组内人的删除操作，如果要对网络中的人进行删除，那么将会复杂很多，仅需要注意删除时对一些group成员变量的更新，并真实的将其删除。

5.BUG

我的BUG

前两次作业在强测与互测中都没有发现BUG，得益于我在课下的测试做得足够充分，第三次作业，时间比较紧，但还算测得比较充分，第三次作业主要是在性能上出了问题，课下我自己测试的时候就发现好像跑的比较慢，查了一下发现迪杰斯特拉求最短路径写得有问题，时间复杂度过高，后来调整了一下调整到标准的迪杰斯特拉算法，可是还是无法满足课程组的要求，需要实现迪杰斯特拉算法的堆优化，导致公测出了问题，另外判断点双连通分量写的也有问题，画蛇添足的判断了每次查找到的路径，在一般情况下可能比较快一点，但在极端情况下会很耗时，也就是说时间复杂度其实变高了。

别人的BUG

前两次作业没能发现别人的BUG，也许是自己做得也比较好的原因，第三次作业就发现了很多低级问题了，有一个同学在添加关系时的异常优先级处理有问题，在person找不到，而两个personId相同时会出问题，因为他的person找不到的优先级不是最高的，他先判断的是两个personId是否相同；还有一个同学的借钱处理得有问题，使用容器不当，应该是索引弄混了，导致正常的借款都会出问题，其实这种BUG简单一测就会发现；另外还有两个同学在找最短路径时不连接时设置的最大路径不够大，比如一个同学设置的仅超过了可能的最大权值一点点，但是最短路径会很多条边加起来，会超过他们设计的“无穷远”；另外还有一个同学的最短路径算法有问题，得不到正确结果，还有一个同学查找stronglink有问题，无法返回正确结果。

6.心得

• 多借鉴现有的算法，多学习，自己写的可靠性可能不高
• 考虑性能时要好好算算自己算法的时间复杂度，要严谨
• 在考虑性能时应该在测试时兼顾自己的时间
• 不要做一些反向“优化”

第三单元总结

标签：技术   算法思路   效果   自动化测试   自己   比较   验证   自己的   学习   

原文地址：https://www.cnblogs.com/c-h-18373205/p/12943496.html