标签:局部最优 自己 应用 lan oid png 统计 决定 粒子
选择,交叉,变异
假设前一个状态为\(x(n)\),系统根据某一规则(比如梯度下降)使状态变为\(x(n+1)\)时,系统的能量(通过损失函数算得)由\(E(n)\)变为E(n+1),定义由\(x(n)\)到\(x(n+1)\)的状态转化的接受概率为:
\(P=\left\{\begin{matrix} 1 & E(n+1)<E(n)\\ e^-{\frac{E(n+1)-E(n)}{T}} & E(n+1)\geqslant E(n) \end{matrix}\right.\)
从上式我们可以看到,如果能量减小了,那么这种转移就被接受(概率为1),如果能量增大了,则以一定的概率被接受,这使得算法有了跳出局部最优的机会
在上面的公式中,可以调节的参数就是T,T如果过小,就会导致退火太快,达到局部最优值就会结束迭代,如果取值较大,则计算时间会增加,实际应用中采用退火温度表,在退火初期采用较大的T值,随着退火的进行,逐步降低
粒子仅具有两个属性:速度和位置,速度决定了粒子移动的方向和快慢。粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。
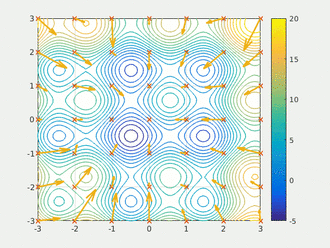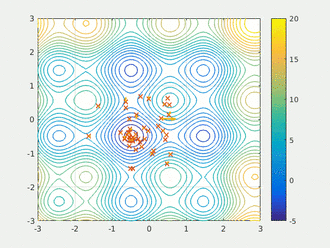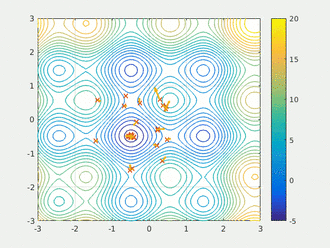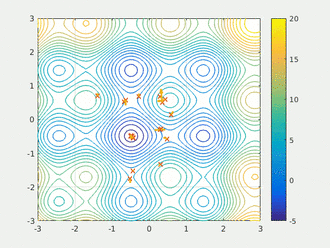


初始化,选择,分布估计,取样产生新种群,选择
这里的分布估计就是根据选择得到的优秀样本,针对指定的分布模型进行极大似然估计。比如均匀分布模型只有一个参数:‘均值’,那么只要统计样本的均值,然后用参数确定的均匀分布来产生新样本就行了。
标签:局部最优 自己 应用 lan oid png 统计 决定 粒子
原文地址:https://www.cnblogs.com/lokvahkoor/p/12949008.html