标签:tin 除了 mem 答案 poj 数据 txt define def
先来讲一讲DFS序是什么东西,直接上图,方便理解。
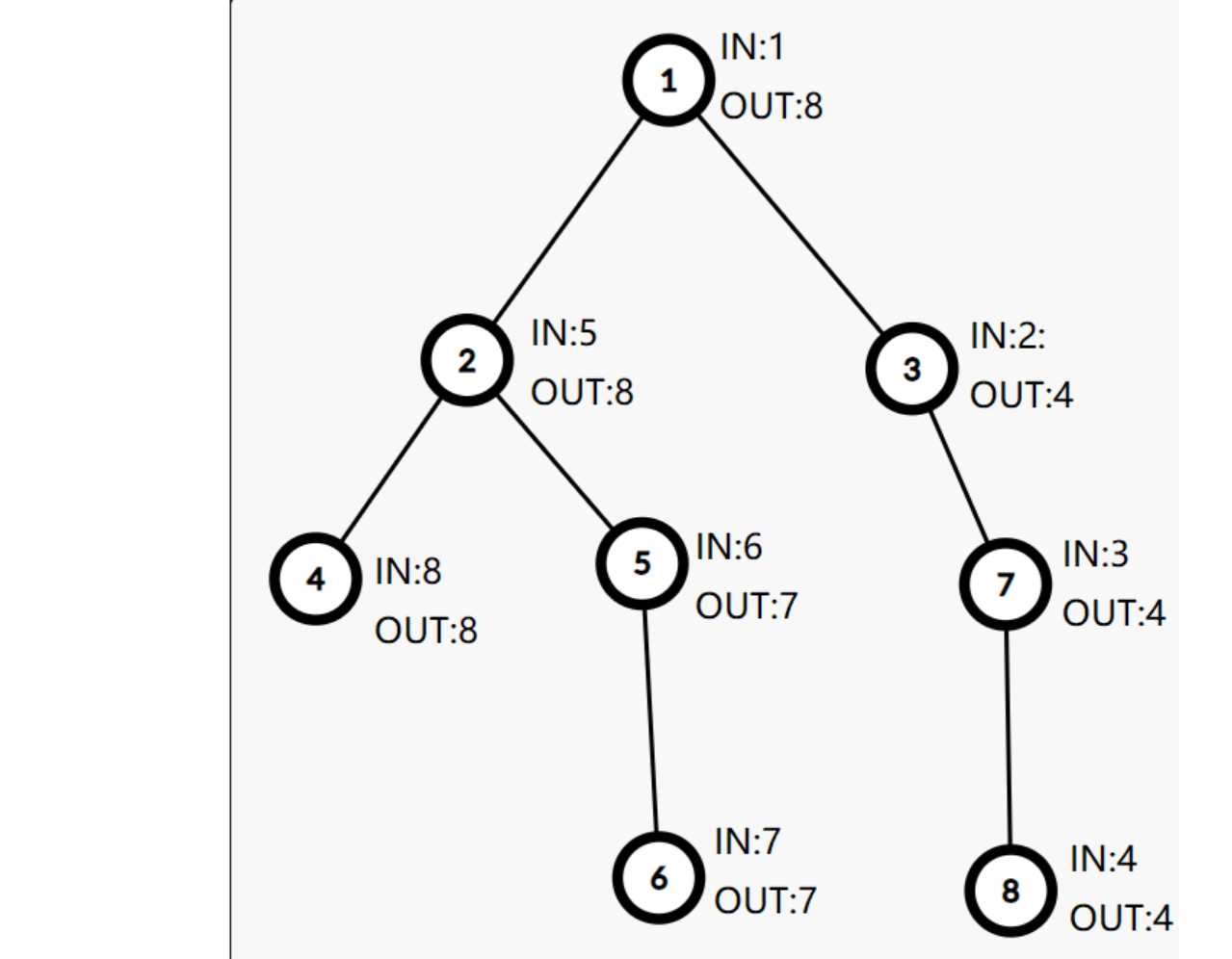
估计巨巨们应该知道了DFS序的两个重要的东西,\(in,out\)数组。
所以我们发现一个节点的子树的遍历是将,刚好是区间\([in, out]\),所以这里我们就可以通过线段树或者树状数组来维护其子树的节点权值以及节点权值的查询。
DFS序的简单问题
对于这个问题,直接对应的就是线段树的单点、区间更新,以及单点、区间查询,直接上一个线段树就行。
简单的\(dfs\)序的应用,然后用树状数组或者线段是维护区间就行,这里树状数组简单些,直接用树状数组了。
// #include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N], tree[N], n, m, tot;
int head[N], to[N << 1], nex[N << 1], cnt;
int in[N], out[N];
char op[10];
void add(int x, int y) {
to[cnt] = y;
nex[cnt] = head[x];
head[x] = cnt++;
}
void update(int pos, int x) {
while(pos <= n) {
tree[pos] += x;
pos += (-pos) & (pos);
}
}
int query(int pos) {
int ans = 0;
while(pos) {
// cout << pos << endl;
ans += tree[pos];
pos -= (-pos) & (pos);
}
return ans;
}
void dfs(int rt, int fa) {
in[rt] = ++tot;
for(int i = head[rt]; ~i; i = nex[i])
if(to[i] != fa)
dfs(to[i], rt);
out[rt] = tot;
}
int main() {
// freopen("in.txt", "r", stdin);
while(scanf("%d", &n) != EOF) {
memset(head, -1, sizeof head);
memset(tree, 0, sizeof tree);
tot = cnt = 0;
int x, y;
for(int i = 1; i < n; i++) {
a[i] = 1;
update(i, 1);
scanf("%d %d", &x, &y);
add(x, y);
add(y, x);
}
dfs(1, 0);
a[n] = 1;
update(n, 1);
scanf("%d", &m);
for(int i = 0; i < m; i++) {
scanf("%s %d", op, &x);
if(op[0] == ‘Q‘) printf("%d\n", query(out[x]) - query(in[x] - 1));
else {
if(a[x]) update(in[x], -1), a[x] = 0;
else update(in[x], 1), a[x] = 1;
}
}
}
return 0;
}
我们先约定一些数组的意义。
| fa | 记录当前Index节点的父节点编号 |
|---|---|
| son | 记录当前Index节点的重儿子编号 |
| sz | 记录当前节点的子树节点个数 |
| dep | 记录当前节点的深度 |
| top | 记录当前节点所在重链的最顶端的节点编号 |
| rk | 记录dfs序为Index的节点编号 |
| id | 记录当前Index节点的dfs序编号 |
第一次DFS
void dfs1(int rt, int f) {
fa[rt] = f, sz[rt] = 1;//记录当前节点的父节点,子树大小。
dep[rt] = dep[f] + 1;//记录当前节点的深度。
for(int i = head[rt]; ~i; i = nex[i]) {
if(to[i] == f) continue;
dfs1(to[i], rt);
sz[rt] += sz[to[i]];//更新子树大小。
if(!son[rt] || sz[to[i]] > sz[son[rt]])
son[rt] = to[i];
//如果当前节点没有重儿子,或者出现了一个节点的子树节点数量大于当前的重儿子的子树节点数量,则更新重儿子。
}
}
上一幅图来理解dfs1更新的结果。
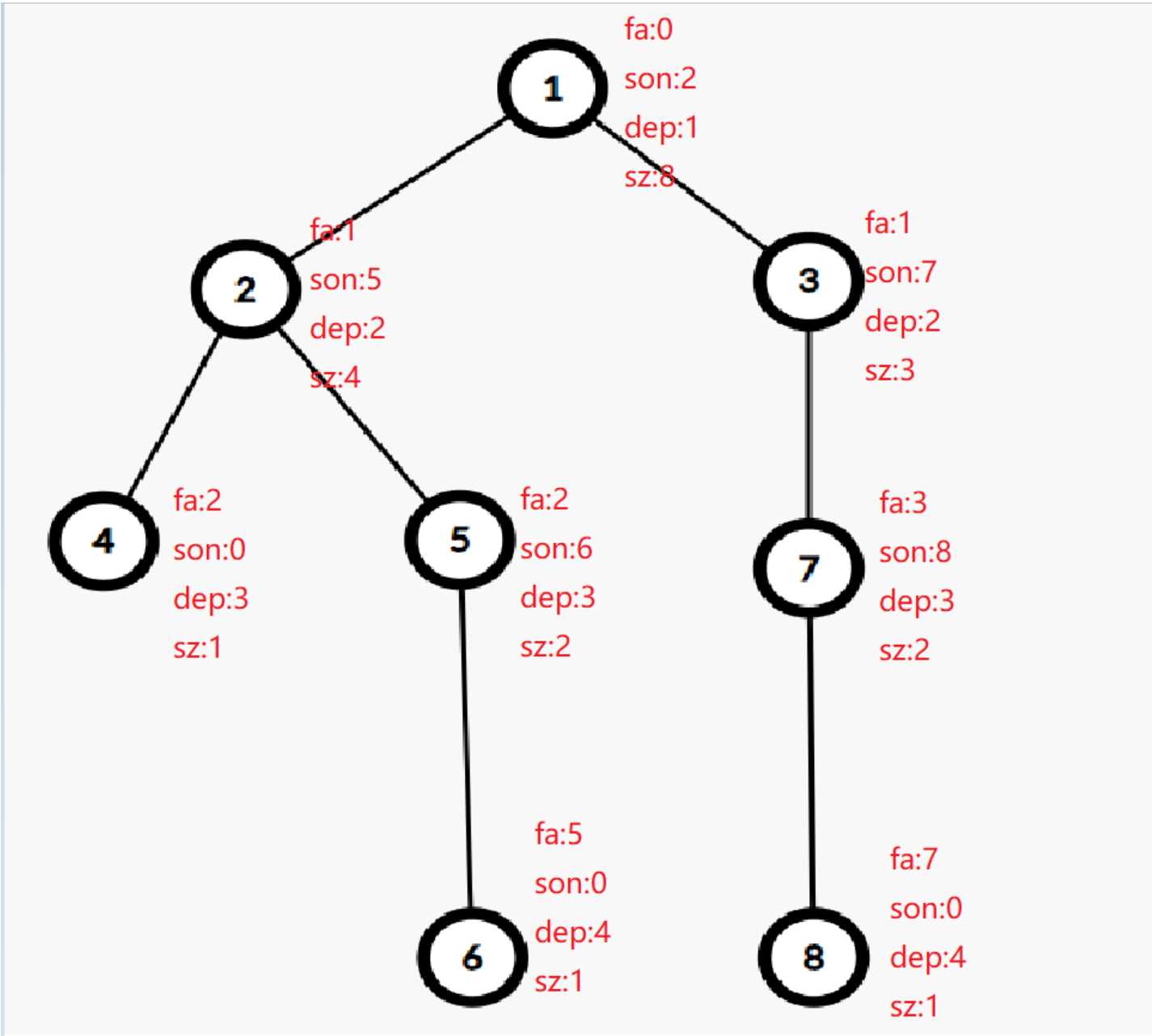
都是常规的更新,应该看图就懂了,唯一可能需要稍微一点点理解的就是son了。
第二次DFS
void dfs2(int rt, int t) {
id[rt] = ++tot;
rk[tot] = rt;
top[rt] = t;//这个更新记录的就是当前节点所在重链的深度最小的节点。
if(!son[rt]) return ;//如果没有重儿子,说明是叶节点,递归边界记得返回。
dfs2(son[rt], t);//优先更新当前所在的重边,
for(int i = head[rt]; ~i; i = nex[i]) {//更新其字节点的重边。
if(to[i] == fa[rt] || to[i] == son[rt]) continue;
dfs2(to[i], to[i]);//与重链间接相连的点一定是一条重链的top节点
}
}
上一幅图来理解dfs2更新的结果,红色的圈起来的是每一条重链。
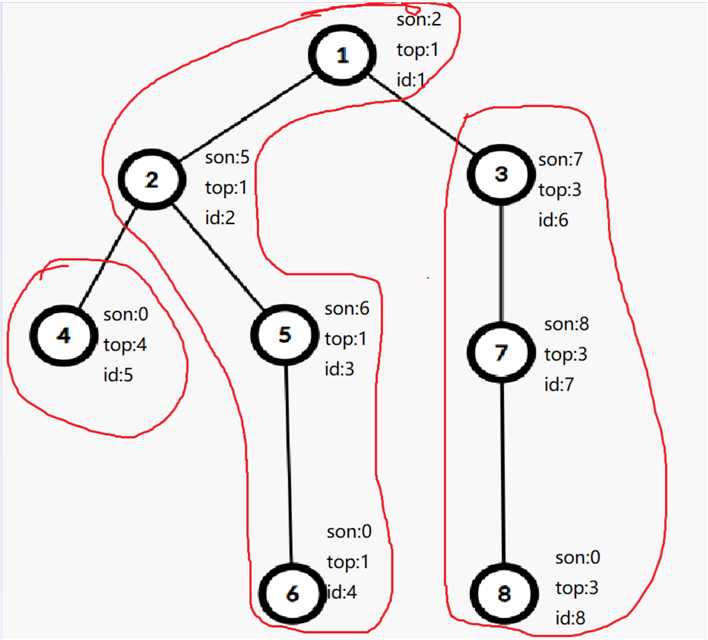
这张图是树链剖分的精髓,把所有的边划分成了,重边和轻边,并且所有的节点依旧持有DFS序的优秀性质,并且一条重链上的dfs序一定是连续的,因此我们同样可以用线段树等数据结构来维护和查询区间。
这里还有一个问题就是dfs2中为什么要先进行,对其重儿子的dfs然后再对其它的儿子进行dfs。
我们要保证top点的延续性,所以我们选择先进行重儿子的dfs。
接下来我们考虑两种操作如何实现
一、将树从x到y结点最短路径上所有节点的权值和
我们的第一想法就是能不能把这两个点,通过转换,变成最后在同一条重链上。
在我们上面记录的变量中,有fa当前节点的父节点编号,所以我们能做的大概好像只有把这个节点向上移动,并且我们每次移动可以跨越一整条重链,到与之相邻的另一条重链,同时我们还可以通过区间和的查询统计每次移动的花费。
从这个方向出发,我们考虑,什么时候哪个节点可以进行这样的操作。
每一次移动的dep[top]都会变小,如果我们让dep[top]更小的去进行这个操作,最后肯定是不可能到达,top = top的,所以我们只有一个选择,移动dep[top]小的节点,只有这样,这两个节点的top才有可能会相同,
举个例子,统计4 -> 6的最短路的节点编号和
显然\(dep[top[4]] = 3 < dep[top[6]] = 1\),所以我们移动,节点4,统计\(sum(id[top[4]], id[4]) = 4\),此时4到了2这个位置,我们发现\(top[2] = top[6]\),直接利用重链的dfs连续性,查询\(sum(id[2], id[6]) = 13\),最后得到\(sum_{ans} = 4 + 13 = 17\)
二、将树从x到y结点最短路径上所有节点的权值加上Z
明白了上面的操作这个就简单了,无非是把区间查询改成区间更新就行了
#include <bits/stdc++.h>
#define mid (l + r >> 1)
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
#define ls rt << 1
#define rs rt << 1 | 1
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
ll sum[N << 2], lazy[N << 2];
int head[N], value[N], nex[N << 1], to[N << 1], cnt;
int fa[N], sz[N], dep[N], id[N], rk[N], son[N], top[N], tot;
int n, m, mod;
void dfs1(int rt, int f) {
dep[rt] = dep[f] + 1;
sz[rt] = 1; fa[rt] = f;
for(int i = head[rt]; ~i; i = nex[i]) {
if(to[i] == f) continue;
dfs1(to[i], rt);
sz[rt] += sz[to[i]];
if(!son[rt] || sz[to[i]] > sz[son[rt]])
son[rt] = to[i];
}
}
void dfs2(int rt, int t) {
top[rt] = t;
id[rt] = ++tot;
rk[tot] = rt;
if(!son[rt])
return ;
dfs2(son[rt], t);
for(int i = head[rt]; ~i; i = nex[i]) {
if(to[i] == fa[rt] || to[i] == son[rt]) continue;
dfs2(to[i], to[i]);
}
}
void updown(int rt, int l, int r) {
if(lazy[rt]) {
sum[ls] = (sum[ls] + (mid - l + 1) * lazy[rt] % mod) % mod;
sum[rs] = (sum[rs] + (r - mid) * lazy[rt] % mod) % mod;
lazy[ls] = (lazy[ls] + lazy[rt]) % mod;
lazy[rs] = (lazy[rs] + lazy[rt]) % mod;
lazy[rt] = 0;
}
}
void build(int rt, int l, int r) {
if(l == r) {
sum[rt] = value[rk[l]];
return ;
}
build(lson);
build(rson);
sum[rt] = (sum[ls] + sum[rs]) % mod;
}
ll query(int rt, int l, int r, int L, int R) {
if(l >= L && r <= R) return sum[rt];
updown(rt, l, r);
ll ans = 0;
if(L <= mid) ans += query(lson, L, R);
if(R > mid) ans += query(rson, L, R);
return ans;
}
void update(int rt, int l, int r, int L, int R, int k) {
if(l >= L && r <= R) {
sum[rt] = (sum[rt] + (r - l + 1) * k % mod) % mod;
lazy[rt] = (lazy[rt] + k) % mod;
return ;
}
updown(rt, l, r);
if(L <= mid) update(lson, L, R, k);
if(R > mid) update(rson, L, R, k);
sum[rt] = (sum[ls] + sum[rs]) % mod;
}
void print(int rt, int l, int r) {
if(l == r) {
printf("%lld\n", sum[rt]);
return ;
}
updown(rt, l, r);
print(lson);
print(rson);
}
void op1(int x, int y, int k) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
update(1, 1, n, id[top[x]], id[x], k);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
update(1, 1, n, id[x], id[y], k);
}
ll op2(int x, int y) {
ll ans = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
ans = (ans + query(1, 1, n, id[top[x]], id[x])) % mod;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
ans = (ans + query(1, 1, n, id[x], id[y])) % mod;
return ans % mod;
}
void op3(int x, int k) {
update(1, 1, n, id[x], id[x] + sz[x] - 1, k);
}
ll op4(int x) {
return query(1, 1, n, id[x], id[x] + sz[x] - 1);
}
void add(int x, int y) {
to[cnt] = y;
nex[cnt] = head[x];
head[x] = cnt++;
}
int main() {
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
memset(head, -1, sizeof head), cnt = 0;
int x, y, rt, op, z;
scanf("%d %d %d %d", &n, &m, &rt, &mod);
for(int i = 1; i <= n; i++)
scanf("%d", &value[i]);
for(int i = 1; i < n; i++) {
scanf("%d %d", &x, &y);
add(x, y);
add(y, x);
}
dfs1(rt, 0);
dfs2(rt, rt);
// int fa[N], son[N], sz[N], id[N], rk[N], tp[N], dep[N], tot;
// for(int i = 1; i <= n; i++)
// printf("%d %d %d %d %d %d\n", fa[i], son[i], sz[i], id[i], top[i], dep[i]);
build(1, 1, n);
// print(1, 1, n);
// puts("");
for(int i = 0; i < m; i++) {
scanf("%d", &op);
if(op == 1) {
scanf("%d %d %d", &x, &y, &z);
op1(x, y, z);
}
else if(op == 2) {
scanf("%d %d", &x, &y);
printf("%lld\n", op2(x, y) % mod);
}
else if(op == 3) {
scanf("%d %d", &x, &y);
op3(x, y);
}
else {
scanf("%d", &x);
printf("%lld\n", op4(x) % mod);
}
}
// print(1, 1, n);
return 0;
}
其实是个模板附赠题,比洛谷模板还简单,就一个操作,区间中每个节点 + 1,然后要注意在最后的答案中,除了第一个被访问的点,其他的ans都要减1处理,然后就完事了。
#include <bits/stdc++.h>
#define mid (l + r >> 1)
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
#define ls rt << 1
#define rs rt << 1 | 1
using namespace std;
typedef long long ll;
const int N = 3e5 + 10;
ll sum[N << 2], lazy[N << 2], ans[N];
int head[N], to[N << 1], nex[N << 1], cnt;
int fa[N], son[N], top[N], sz[N], dep[N], rk[N], id[N], tot;
int n, a[N];
void add(int x, int y) {
to[cnt] = y;
nex[cnt] = head[x];
head[x] = cnt++;
}
void dfs1(int rt, int f) {
fa[rt] = f, sz[rt] = 1;
dep[rt] = dep[f] + 1;
for(int i = head[rt]; ~i; i = nex[i]) {
if(to[i] == f) continue;
dfs1(to[i], rt);
sz[rt] += sz[to[i]];
if(!son[rt] || sz[to[i]] > sz[son[rt]])
son[rt] = to[i];
}
}
void dfs2(int rt, int t) {
top[rt] = t;
id[rt] = ++tot;
rk[tot] = rt;
if(!son[rt]) return ;
dfs2(son[rt], t);
for(int i = head[rt]; ~i; i = nex[i]) {
if(to[i] == fa[rt] || to[i] == son[rt]) continue;
dfs2(to[i], to[i]);
}
}
void push_down(int rt, int l, int r) {
if(lazy[rt]) {
lazy[ls] += lazy[rt];
lazy[rs] += lazy[rt];
sum[ls] += lazy[rt] * (mid - l + 1);
sum[rs] += lazy[rt] * (r - mid);
lazy[rt] = 0;
}
}
void update(int rt, int l, int r, int L, int R) {
if(l >= L && r <= R) {
lazy[rt] += 1;
sum[rt] += r - l + 1;
return ;
}
push_down(rt, l, r);
if(L <= mid) update(lson, L, R);
if(R > mid) update(rson, L, R);
sum[rt] = sum[ls] + sum[rs];
}
void query(int rt, int l, int r) {
if(l == r) {
ans[rk[l]] = sum[rt];
return ;
}
push_down(rt, l, r);
query(lson);
query(rson);
}
void update_tree(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
update(1, 1, n, id[top[x]], id[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
update(1, 1, n, id[x], id[y]);
}
int main() {
// freopen("in.txt", "r", stdin);
memset(head, -1, sizeof head);
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
int x, y;
for(int i = 1; i < n; i++) {
scanf("%d %d", &x, &y);
add(x, y);
add(y, x);
}
dfs1(1, 0);
dfs2(1, 0);
for(int i = 1; i < n; i++)
update_tree(a[i], a[i + 1]);
query(1, 1, n);
for(int i = 2; i <= n; i++)
ans[a[i]]--;
for(int i = 1; i <= n; i++)
printf("%lld\n", ans[i]);
return 0;
}
标签:tin 除了 mem 答案 poj 数据 txt define def
原文地址:https://www.cnblogs.com/lifehappy/p/12944963.html