标签:技术 res max -- 用例 roman 算法实现 最大堆 选择
数据结构与算法实验报告
修理牧场
姓名:孙瑞霜
一、实验目的
1、熟练掌握学习的每种结构及其相应算法;
2、理论联系实际,会对现实问题建模并设计相应算法。
3、优化算法,使得算法效率适当提高
二、实验要求:
1. 认真阅读和掌握教材上和本实验相关的内容和算法;
2. 上机将各种相关算法实现;
3. 实现上面实验目的要求的功能,并能进行简单的验证。
三、实验内容
认真学习 学习通->数据结构->资料->数据结构实验指导书--陈越版,从第二章进阶实验1~10中任选一个来实现,编写程序,输入给定的数据,能得到给定的输出。总结算法思想、画出流程图,并思考程序有无改进空间,如何改进。
三、算法描述
(采用自然语言描述)
选择了“修理牧场”
改进后方法二:我们将木头的长度看成树的节点,每切割一次木头就相当与把节点分为两个子节点,每个节点的权值就相当于分的的木头长度。那么最后这棵树的总权值就相当于切割的代价。问题就变成求这棵树的最小权值,这不就是Hoffman树的作用嘛。所以这道题目就变成了求一棵Hoffman树的权值。(选用两种方法)
四、详细设计
(画出程序流程图)
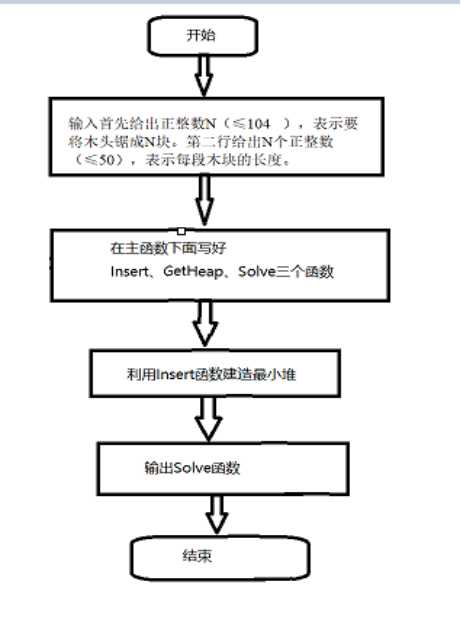
五、程序代码
(给出必要注释)
(方法一)复杂代码
#include<stdio.h>
#include<stdlib.h>
#define MinData 0
//#define M 10000
#define MaxData 100
typedef struct TreeNode *HuffmanTree;
struct TreeNode{
//char Data;
int Weight;
HuffmanTree Left;
HuffmanTree Right;
};
typedef HuffmanTree ElementType;
typedef struct HeapStruct *MinHeap;
struct HeapStruct {
ElementType *Elements; /* 存储堆元素的数组 */
int Size; /* 堆的当前元素个数 */
int Capacity; /* 堆的最大容量 */
};
//函数声明
MinHeap Create( int MinSize );
void Insert( MinHeap H, ElementType item );
ElementType DeleteMin( MinHeap H );
MinHeap BuildMinHeap( MinHeap H );
int IsFull( MinHeap H );
int IsEmpty( MinHeap H );
void printfHeap( MinHeap H);
HuffmanTree Huffman( MinHeap H );
int PreOrderTraversal( HuffmanTree H,int sum );
MinHeap Create( int MaxSize )
{ /* 创建容量为MinSize的空的最小堆 */
HuffmanTree ht0;
MinHeap H =( MinHeap)malloc( sizeof( struct HeapStruct ) );
H->Elements =( ElementType *) malloc( (MaxSize+1) * sizeof( ElementType ) );
H->Size = 0;
H->Capacity =MaxSize;
/* 定义"哨兵"为小于堆中所有可能元素的值*/
ht0 = (HuffmanTree)malloc( sizeof( struct TreeNode) );
ht0->Left = NULL;
ht0->Right = NULL;
ht0->Weight = 0;
H->Elements[0] = ht0;
return H;
}
void printfHeap( MinHeap H)
{
int i;
for(i=1;i<=H->Size;i++)
printf("%d ",H->Elements[i]->Weight);
}
void Insert( MinHeap H, ElementType item )
{ /* 将元素item 插入最小堆H,其中H->Elements[0]已经定义为哨兵 */
int i;
HuffmanTree hti;
if ( IsFull(H) ) {
printf("最小堆已满");
return;
}
hti = (HuffmanTree)malloc( sizeof( struct TreeNode) );
hti->Left = item->Left;
hti->Right = item->Right;
hti->Weight = item->Weight;
i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
for ( ; H->Elements[i/2]->Weight > item->Weight; i/=2 )
H->Elements[i] = H->Elements[i/2]; /* 向下过滤结点 */
H->Elements[i] = hti; /* 将item 插入 */
}
ElementType DeleteMin( MinHeap H )
{ /* 从最大堆H中取出键值为最大的元素,并删除一个结点 */
int Parent, Child;
ElementType MinItem, temp;
if ( IsEmpty(H) ) {
printf("最大堆已为空");
return H->Elements[0];
}
MinItem = H->Elements[1]; /* 取出根结点最小值 */
/* 用最小堆中最后一个元素从根结点开始向上过滤下层结点 */
temp = H->Elements[H->Size--];
for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!= H->Size) && (H->Elements[Child]->Weight > H->Elements[Child+1]->Weight) )
Child++; /* Child指向左右子结点的较小者 */
if( temp->Weight <= H->Elements[Child]->Weight ) break;
else /* 移动temp元素到下一层 */
H->Elements[Parent] = H->Elements[Child];
}
H->Elements[Parent] = temp;
return MinItem;
}
MinHeap BuildMinHeap( MinHeap H )
{ /* 这里假设所有H->Size个元素已经存在H->Elements[]中 */
/* 本函数将H->Elements[]中的元素调整,使满足最小堆的有序性 */
int Parent, Child, i;
ElementType temp;
for( i = H->Size/2; i>0; i-- ){ /*从最后一个结点的父结点开始 */
temp = H->Elements[i];
for( Parent=i; Parent*2<=H->Size; Parent=Child ) { /* 向下过滤 */
Child = Parent * 2;
if( (Child!= H->Size) && (H->Elements[Child]->Weight > H->Elements[Child+1]->Weight) )
Child++; /* Child指向左右子结点的较小者 */
if( temp->Weight <= H->Elements[Child]->Weight ) break;
else /* 移动temp元素到下一层 */
H->Elements[Parent] = H->Elements[Child];
} /* 结束内部for循环对以H->Elements[i]为根的子树的调整 */
H->Elements[Parent] = temp;
}
return H;
}
int IsFull( MinHeap H )
{
if(H->Size == H->Capacity -1)
return 1;
else
return 0;
}
int IsEmpty( MinHeap H )
{
if(H->Size == 0)
return 1;
else
return 0;
}
int main()
{
MinHeap h1;
int i;
int num;
HuffmanTree ht;
int M;
scanf("%d",&M);
h1=Create(M);
//printf("请输入序列:\n");
for(i=1;i<=M;i++)
{
scanf(" %d",&num);
ht = (HuffmanTree)malloc( sizeof( struct TreeNode) );
ht ->Left = NULL;
ht->Right = NULL;
ht->Weight = num;
h1->Elements[i]=ht;
h1->Size++;
}
ht=Huffman(h1);
printf("%d\n",PreOrderTraversal(ht,0));
}
HuffmanTree Huffman( MinHeap H )
{ /* 假设根据H->Size个权值所生成的跟结点已经存在H->Elements[]里 */
int i,m;
HuffmanTree T;
BuildMinHeap(H); /*将H->Elements[]按权值调整为最小堆*/
m=H->Size;
for (i = 1; i < m; i++) { /*做H->Size -1次合并*/
T = (HuffmanTree)malloc( sizeof( struct TreeNode) ); /*建立一个新的根结点*/
T->Left = DeleteMin(H);/*从最小堆中删除一个结点,作为新T的左子结点*/
T->Right = DeleteMin(H); /*从最小堆中删除一个结点,作为新T的右子结点*/
T->Weight = T->Left->Weight+T->Right->Weight; /*计算新权值*/
Insert( H, T ); /*将新T插入最小堆*/
}
T=DeleteMin(H);//取合并后的树根
return T;
}
//递归先序求哈夫曼树的非叶子结点的权重和
int PreOrderTraversal(HuffmanTree T,int sum)
{
if(T)
{
if(T->Left&&T->Right)
sum+=T->Weight;
sum= PreOrderTraversal(T->Left,sum);
sum=PreOrderTraversal(T->Right,sum);
}
return sum;
}
(方法二)优化后代码
#include<stdio.h>
#define swap(a,b) a=a^b,b=a^b,a=a^b
int tail=0; //堆的最后一个元素的下一个位置
void Insert(int *length,int temp);
int GetHeap(int *length);
int Solve(int *length);
int main(void)
{
int N;
int i;
scanf("%d",&N);
int length[N];
int temp;
for(i=0;i<N;i++){
scanf("%d",&temp);
Insert(length,temp); //构造一个小顶堆
}
printf("%d",Solve(length));
return 0;
}
void Insert(int *length,int temp)
{
int son,father;
son=tail;
length[tail++]=temp;
father=(son+(son&1))/2-1;
if(!son)
return ;
while(length[son]<length[father]&&father>=0){
swap(length[son],length[father]); //交换两节点位置
son=father;
father=(father+(father&1))/2-1;
}
return ;
}
int GetHeap(int *length)
{
int result=length[0];
int father=0;
int son=1;
length[0]=length[--tail];
while(son<tail){
if(length[son]>length[son+1])
son++; //如果左孩子节点的数值更大
if(length[father]>length[son]){
swap(length[father],length[son]);
father=son;
son=2*son+1;
}
else
break;
}
return result;
}
int Solve(int *length)
{
int min1,min2;
int result=0;
if(tail==1)
return 0;
while(1!=tail){
min1=GetHeap(length);
min2=GetHeap(length); //找打最小的两块板子
result+=min1+min2; //将其合为一块板子
Insert(length,min1+min2); //继续排序
}
return result;
}
六、测试和结果
(给出测试用例以及测试结果)
输入样例:
8
4 5 1 2 1 3 1 1
输出样例:49
七、用户手册
首先打开Dev,然后将代码粘贴到上面,先编译看是否编译成功,再根据下面测试的数据将代码运行后依次填入,便能得出相应的结果,当然也可以尝试用其他测试数据来测验一下,看看最后结果如何。
标签:技术 res max -- 用例 roman 算法实现 最大堆 选择
原文地址:https://www.cnblogs.com/srs7665/p/12949147.html